Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ke, Junhao
Williamson, N.
Armfield, S.W.
Komiya, A.
and
Norris, S.E.
2021.
High Grashof number turbulent natural convection on an infinite vertical wall.
Journal of Fluid Mechanics,
Vol. 929,
Issue. ,
Addona, Fabio
Chiapponi, Luca
and
Archetti, Renata
2021.
Velocity and density measurements in forced fountains with negative buoyancy.
Physics of Fluids,
Vol. 33,
Issue. 5,
Xia, Yaowen
Gao, Wenfeng
Liu, Tao
Lin, W.
Li, Qiong
and
Li, Jingjin
2022.
Penetration height of weak axisymmetric fountain in homogeneous fluid under the combined temperature and salinity effect.
AIP Advances,
Vol. 12,
Issue. 3,
Obligado, M.
Klein, S.
and
Vassilicos, J. C.
2022.
Interaction of two axisymmetric turbulent wakes.
Physical Review Fluids,
Vol. 7,
Issue. 11,
Long, Yanguang
Wang, Jinjun
and
Pan, Chong
2022.
Universal modulations of large-scale motions on entrainment of turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 941,
Issue. ,
Sahebjam, Rana
Kohan, Khashayar F.
and
Gaskin, Susan
2022.
The dynamics of an axisymmetric turbulent jet in ambient turbulence interpreted from the passive scalar field statistics.
Physics of Fluids,
Vol. 34,
Issue. 1,
Xia, Y.
Liu, T.
Gao, W.
Lin, W.
Li, Q.
and
Ding, X.
2022.
Behavior of weak axisymmetric fountain in homogeneous fluid with coexistent temperature and concentration effects.
Case Studies in Thermal Engineering,
Vol. 36,
Issue. ,
p.
102204.
Jordan, Owen H.
Rooney, Gabriel G.
Devenish, Benjamin J.
and
van Reeuwijk, Maarten
2022.
Under pressure: turbulent plumes in a uniform crossflow.
Journal of Fluid Mechanics,
Vol. 932,
Issue. ,
Bempedelis, Nikolaos
Laizet, Sylvain
and
Deskos, Georgios
2023.
Turbulent entrainment in finite-length wind farms.
Journal of Fluid Mechanics,
Vol. 955,
Issue. ,
Brizzolara, Stefano
Mollicone, Jean-Paul
van Reeuwijk, Maarten
and
Holzner, Markus
2023.
Entrainment at multi-scales in shear-dominated and Rayleigh–Taylor turbulence.
European Journal of Mechanics - B/Fluids,
Vol. 101,
Issue. ,
p.
294.
Zhang, Xinxian
Watanabe, Tomoaki
and
Nagata, Koji
2023.
Reynolds number dependence of the turbulent/non-turbulent interface in temporally developing turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 964,
Issue. ,
Huang, Jingzi
Burridge, Henry C.
and
van Reeuwijk, Maarten
2023.
The internal structure of forced fountains.
Journal of Fluid Mechanics,
Vol. 961,
Issue. ,
Rowell, C. R.
Jellinek, A. M.
and
Gilchrist, J. T.
2023.
Tracking Eruption Column Thermal Evolution and Source Unsteadiness in Ground‐Based Thermal Imagery Using Spectral‐Clustering.
Geochemistry, Geophysics, Geosystems,
Vol. 24,
Issue. 11,
Huang, Jingzi
Burridge, Henry C.
and
van Reeuwijk, Maarten
2023.
Local entrainment across a TNTI and a TTI in a turbulent forced fountain.
Journal of Fluid Mechanics,
Vol. 977,
Issue. ,
Xie, Yuanliang
Zhang, Xinxian
Xiong, Xue-Lu
and
Zhou, Yi
2024.
Temporal evolution of the turbulence interface of a turbulent plane jet.
Journal of Fluid Mechanics,
Vol. 1001,
Issue. ,
Huang, Jingzi
Burridge, Henry C.
de Roode, Stephan R.
and
van Reeuwijk, Maarten
2025.
Entrainment and detrainment statistics of a stationary shallow cumulus cloud.
Quarterly Journal of the Royal Meteorological Society,
Vol. 151,
Issue. 767,
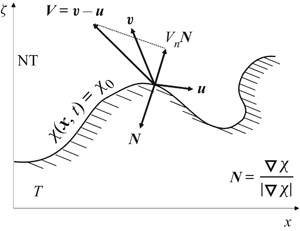
 $\bar {V}_g$ to be the fluid motion across an isosurface of an averaged scalar, we find that for a slender flow,
$\bar {V}_g$ to be the fluid motion across an isosurface of an averaged scalar, we find that for a slender flow,  $\bar {V}_g=\bar {u}_\zeta - \bar {\textrm {D}}h_t/\bar {\textrm {D}}t$, where
$\bar {V}_g=\bar {u}_\zeta - \bar {\textrm {D}}h_t/\bar {\textrm {D}}t$, where  $\bar {\textrm {D}}/\bar {\textrm {D}} t$ is the material derivative of the average flow field and
$\bar {\textrm {D}}/\bar {\textrm {D}} t$ is the material derivative of the average flow field and  $\bar {u}_\zeta$ is the average velocity perpendicular to the flow direction across the interface located at
$\bar {u}_\zeta$ is the average velocity perpendicular to the flow direction across the interface located at  $\zeta =h_t$. The description is shown to reproduce well-known results for the axisymmetric jet, the planar wake and the temporal jet, and provides a clear link between the local (small scale) and global (integral) descriptions of turbulent entrainment. Application to unsteady jets/plumes demonstrates that, under unsteady conditions, the entrainment coefficient
$\zeta =h_t$. The description is shown to reproduce well-known results for the axisymmetric jet, the planar wake and the temporal jet, and provides a clear link between the local (small scale) and global (integral) descriptions of turbulent entrainment. Application to unsteady jets/plumes demonstrates that, under unsteady conditions, the entrainment coefficient  $\alpha$ no longer only captures entrainment of ambient fluid, but also time-dependency effects due to the loss of self-similarity.
$\alpha$ no longer only captures entrainment of ambient fluid, but also time-dependency effects due to the loss of self-similarity.