1. Introduction
Infragravity waves of frequency 0.004–0.04 Hz were first identified outside the surf zone by Munk (Reference Munk1949) and Tucker (Reference Tucker1950) from field observations. Since then, numerous researches have confirmed that infragravity waves can be a dominant forcing factor for nearshore water motion (Stockdon et al. Reference Stockdon, Holman, Howd and Sallenger2006), coastal inundation (Cheriton, Storlazzi & Rosenberger Reference Cheriton, Storlazzi and Rosenberger2016; Henderson et al. Reference Henderson, Fiedler, Merrifield, Guza and Young2022) and sediment transport (Roelvink et al. Reference Roelvink, Reniers, van Dongeren, van Thiel de Vries, McCall and Lescinski2009; Palmsten & Splinter Reference Palmsten and Splinter2016). Infragravity waves may cause resonant response of harbours (Diaz-Hernandez et al. Reference Diaz-Hernandez, Mendez, Losada, Camus and Medina2015), marine structures (Zhao et al. Reference Zhao, Li, Zou, Han and Geng2022) and ice shelves (Bromirski et al. Reference Bromirski, Chen, Stephen, Gerstoft, Arcas, Diez, Aster, Wiens and Nyblade2017). Readers are referred to Bertin et al. (Reference Bertin2018) for a full review of the generation mechanisms and impacts of infragravity waves.
A ubiquitous mechanism for the generation of nearshore infragravity waves is the second-order nonlinear forcing of short-wave groups. Longuet-Higgins & Stewart (Reference Longuet-Higgins and Stewart1962) (hereafter referred to as Reference Longuet-Higgins and StewartLHS62) showed that infragravity waves of the scale of short-wave groups are induced by nonlinear group forcing through the wave radiation stress gradient. Study Reference Longuet-Higgins and StewartLHS62 provided an equilibrium solution for one-dimensional (1-D) group-induced infragravity waves on a flat bottom, which is the bound subharmonic in antiphase with the group. The equilibrium solutions for the two-dimensional counterpart were proposed by Hasselmann (Reference Hasselmann1962) and McAllister et al. (Reference McAllister, Adcock, Taylor and van den Bremer2017).
As wave groups propagate over variable depth, however, the equilibrium solution is no longer valid. For instance, with diminishing depth on a sloping beach towards the shore, the incident bound infragravity waves increasingly lag behind wave groups and gain more energy through nonlinear interaction with wave groups outside the surf zone, as observed in laboratory experiments (Van Leeuwen Reference Van Leeuwen1992; Janssen, Battjes & van Dongeren Reference Janssen, Battjes and van Dongeren2003; Guérin, de Bakker & Bertin Reference Guérin, de Bakker and Bertin2019), numerical modelling (List Reference List1992; Melito et al. Reference Melito, Parlagreco, Devoti and Brocchini2022; Liu et al. Reference Liu, Yao, Liao, Li, Zhang and Zou2023) and field experiments (Elgar & Guza Reference Elgar and Guza1985; Masselink Reference Masselink1995; Contardo & Symonds Reference Contardo and Symonds2013; Inch et al. Reference Inch, Davidson, Masselink and Russell2017). This process of energy transfer from primary waves to infragravity waves is subject to offshore wave conditions and tidal modulation of local depth (Thomson et al. Reference Thomson, Elgar, Raubenheimer, Herbers and Guza2006; Bertin et al. Reference Bertin, Martins, de Bakker, Chataigner, Guérin, Coulombier and de Viron2020) even in a microtidal environment (Melito et al. Reference Melito, Parlagreco, Devoti and Brocchini2022). The key indicator of the occurrence of energy transfer is the non-equilibrium phase coupling between infragravity waves and wave groups due to the presence of additional infragravity waves that lag the equilibrium bound subharmonic by ![]() ${\rm \pi} /2$. In intermediate water, the additional wave manifests itself as a bound subharmonic induced by the perturbation of the bottom slope (Bowers Reference Bowers1992; Van Leeuwen Reference Van Leeuwen1992; Janssen et al. Reference Janssen, Battjes and van Dongeren2003; Zou Reference Zou2011); in shallow water, it is interpreted as a free subharmonic (Mei & Benmoussa Reference Mei and Benmoussa1984; Nielsen & Baldock Reference Nielsen and Baldock2010; Moura & Baldock Reference Moura and Baldock2019; Contardo et al. Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and Symonds2021). Free infragravity waves can also be generated in the surf zone as dynamic wave-induced set-up through the moving-breakpoint forcing mechanism (Symonds, Huntley & Bowen Reference Symonds, Huntley and Bowen1982; Contardo, Symonds & Dufois Reference Contardo, Symonds and Dufois2018).
${\rm \pi} /2$. In intermediate water, the additional wave manifests itself as a bound subharmonic induced by the perturbation of the bottom slope (Bowers Reference Bowers1992; Van Leeuwen Reference Van Leeuwen1992; Janssen et al. Reference Janssen, Battjes and van Dongeren2003; Zou Reference Zou2011); in shallow water, it is interpreted as a free subharmonic (Mei & Benmoussa Reference Mei and Benmoussa1984; Nielsen & Baldock Reference Nielsen and Baldock2010; Moura & Baldock Reference Moura and Baldock2019; Contardo et al. Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and Symonds2021). Free infragravity waves can also be generated in the surf zone as dynamic wave-induced set-up through the moving-breakpoint forcing mechanism (Symonds, Huntley & Bowen Reference Symonds, Huntley and Bowen1982; Contardo, Symonds & Dufois Reference Contardo, Symonds and Dufois2018).
For wave groups in intermediate water depth over a mildly sloping bottom, Janssen et al. (Reference Janssen, Battjes and van Dongeren2003) and Zou (Reference Zou2011) obtained analytical solutions to the 1-D linearised shallow water equation with a forcing term of radiation stress curvature through the perturbation approach. The off-resonant solution of Janssen et al. (Reference Janssen, Battjes and van Dongeren2003) shows that the phase lag of the infragravity wave with respect to group forcing shifts away from ![]() ${\rm \pi}$ toward
${\rm \pi}$ toward ![]() $1.5{\rm \pi}$ as depth decreases. Using a multiscale Wentzel–Kramers–Brillouin expansion method, Zou (Reference Zou2011) proposed a second-order analytical solution that is the sum of an equilibrium bound subharmonic described by the Reference Longuet-Higgins and StewartLHS62 solution for flat bottom, a topography-induced bound subharmonic in quadrature with the Reference Longuet-Higgins and StewartLHS62 solution and two free subharmonics propagating in opposite directions due to scattering at the edge of finite topography.
$1.5{\rm \pi}$ as depth decreases. Using a multiscale Wentzel–Kramers–Brillouin expansion method, Zou (Reference Zou2011) proposed a second-order analytical solution that is the sum of an equilibrium bound subharmonic described by the Reference Longuet-Higgins and StewartLHS62 solution for flat bottom, a topography-induced bound subharmonic in quadrature with the Reference Longuet-Higgins and StewartLHS62 solution and two free subharmonics propagating in opposite directions due to scattering at the edge of finite topography.
As the group propagating velocity approaches the free long-wave propagating velocity in shallow water, resonance occurs between group forcing and subharmonics propagating in the same direction as wave groups, causing the solutions based on the perturbation method to diverge. In this case, implicit solutions in integral form were derived by Symonds et al. (Reference Symonds, Huntley and Bowen1982), Van Leeuwen (Reference Van Leeuwen1992) and Schäffer (Reference Schäffer1993) for a plane beach, and by Liao et al. (Reference Liao, Li, Liu and Zou2021) for arbitrary topography with a mildly sloping bottom. The near-resonant solution of Liao et al. (Reference Liao, Li, Liu and Zou2021) indicates that, with diminishing depth on a plane beach, the group-induced subharmonic asymptotically leads the group forcing by ![]() ${\rm \pi} /2$ at leading order, and its amplitude increases as
${\rm \pi} /2$ at leading order, and its amplitude increases as ![]() $\propto h^{-1}$ (
$\propto h^{-1}$ (![]() $h$ = depth), a shoaling rate lower than the shallow-water limit of the Reference Longuet-Higgins and StewartLHS62 solution (
$h$ = depth), a shoaling rate lower than the shallow-water limit of the Reference Longuet-Higgins and StewartLHS62 solution (![]() $\propto h^{-2.5}$) but higher than the free infragravity wave growth rate (
$\propto h^{-2.5}$) but higher than the free infragravity wave growth rate (![]() $\propto h^{-0.25}$, known as Green's law; Green Reference Green1838). Contardo et al. (Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and Symonds2021) (hereinafter Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and SymondsCLHRDS21) proposed an alternative solution for shallow water of variable depth, by discretising the topography into many steps, and applying the Reference Longuet-Higgins and StewartLHS62 solution on both sides of each step to derive the free subharmonics scattered due to the abrupt depth change. Study Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and SymondsCLHRDS21 derived the total subharmonic as the superposition of the local bound subharmonic given by the Reference Longuet-Higgins and StewartLHS62 solution and the free subharmonics scattered from all the steps through which the wave groups have travelled.
$\propto h^{-0.25}$, known as Green's law; Green Reference Green1838). Contardo et al. (Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and Symonds2021) (hereinafter Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and SymondsCLHRDS21) proposed an alternative solution for shallow water of variable depth, by discretising the topography into many steps, and applying the Reference Longuet-Higgins and StewartLHS62 solution on both sides of each step to derive the free subharmonics scattered due to the abrupt depth change. Study Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and SymondsCLHRDS21 derived the total subharmonic as the superposition of the local bound subharmonic given by the Reference Longuet-Higgins and StewartLHS62 solution and the free subharmonics scattered from all the steps through which the wave groups have travelled.
However, the transition of group-induced subharmonic from weak resonance in intermediate depth to strong resonance in shallow water is currently not well understood, because there is no clear dividing line between the parameter regimes of the above-mentioned models. This deficit directly leads to a debate on the releasing process of bound subharmonics in shallow water. More specifically, it is often assumed that the group-bounded subharmonic is released when the primary waves begin to break (e.g. Masselink Reference Masselink1995; Bertin et al. Reference Bertin2018), while Baldock (Reference Baldock2012) argued that it is released when the group velocity equalled shallow water wave velocity so that resonance occurs, regardless of wave breaking. In addition to the releasing condition, the underlying mechanism for the transition from bound subharmonic to free mode during the releasing process also remains unclear.
To understand the mutual transition between group-induced subharmonics in weak and strong resonance, it is necessary to unify the aforementioned theoretical solutions in order to provide a holistic view of the physical process of the generation of group-induced subharmonics at all water depths. Although the general form of the solution for group-induced subharmonics over 1-D topography was derived by Schäffer (Reference Schäffer1993) by the method of variation of parameters (equation (4.10) therein), it was only applied to the special case of bichromatic waves normally incident on a plane beach, leaving its consistency with existing solutions and, more importantly, its physical interpretation unaddressed. This issue is crucial for understanding the behaviour of group-induced subharmonics at all water depths, which forms the motivation and focus of the present study.
In the present work, the solution of group-induced subharmonics is derived based on the Green's function method for the first time, which allows for a novel consistent physical interpretation of generating mechanisms of group-induced subharmonics at all water depths. Green's function is the response function of a linear system to a unit forcing at a point in space or time (Duffy Reference Duffy2015). It is a flexible and powerful mathematical tool for solving non-homogeneous linear differential equations. The forcing term of the equation is treated as spatially distributed unit point forcing weighted by local forcing and thus the response is the weighted linear superposition of responses to all unit point forcing. Green's function has been applied in a wide range of problems related to water waves, including harbour resonance (Miles Reference Miles1974), internal waves (Voisin Reference Voisin1991), waves over continental shelf (Miles Reference Miles1972), wave–structure interactions (Telste & Noblesse Reference Telste and Noblesse1986; Wang, Ning & Zou Reference Wang, Ning and Zou2020) and numerous studies based on the boundary element method (e.g. Longuet-Higgins & Cokelet Reference Longuet-Higgins and Cokelet1976; Liu et al. Reference Liu, Mukherjee, Nishimura, Schanz, Ye, Sutradhar, Pan, Dumont, Frangi and Saez2011; Ning et al. Reference Ning, Shi, Zou and Teng2015; Zheng et al. Reference Zheng, Lin, Li, Adcock, Li and van den Bremer2020). Using the present generalised solution proposed, existing solutions (Longuet-Higgins & Stewart Reference Longuet-Higgins and Stewart1962; Van Leeuwen Reference Van Leeuwen1992; Schäffer Reference Schäffer1993; Janssen et al. Reference Janssen, Battjes and van Dongeren2003; Zou Reference Zou2011; Contardo et al. Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and Symonds2021; Liao et al. Reference Liao, Li, Liu and Zou2021) for non-breaking waves are unified. Physically, the solution treats the group-forcing field as a sum of force pulses distributed in time and space, which constantly emit free waves away from each spatial point in the wave field. It is shown that the group-induced subharmonic, previously taken as the sum of bound and free subharmonics, may be interpreted as the results of the emission, propagation and interference of all the free subharmonics generated by the point forcing in the domain.
In the following, we first describe the problem considered and introduce the governing equations in § 2. In § 3, the unified solution of the group-induced subharmonic is derived based on Green's function, along with the physical interpretation of its behaviour in intermediate and shallow water. Unification of existing solutions through the present solution is shown in § 4. Discussions on the generation and formation of group-induced subharmonic from the perspective of Green's function, the influence of topography, the effect of moving-breakpoint forcing and possible extensions of the solution are presented in §§ 5 and 6. Main conclusions are drawn in § 7.
2. Governing equations
By introducing the concept of radiation stress to represent the phase-averaged residual momentum flux due to the presence of waves, Reference Longuet-Higgins and StewartLHS62 proposed the theory of low-frequency subharmonic induced by the nonlinear group forcing of radiation stress. For regular waves under non-breaking conditions, the radiation stress ![]() $S$ accurate to second order in wave steepness is expressed as (Longuet-Higgins & Stewart Reference Longuet-Higgins and Stewart1960)
$S$ accurate to second order in wave steepness is expressed as (Longuet-Higgins & Stewart Reference Longuet-Higgins and Stewart1960)
where ![]() $E$ denotes the wave energy,
$E$ denotes the wave energy, ![]() $c_g$ is the wave group velocity and
$c_g$ is the wave group velocity and ![]() $c$ is the wave phase speed.
$c$ is the wave phase speed.
Consider a unidirectional bichromatic wave group propagating in the positive direction of ![]() $x$ with the surface elevation
$x$ with the surface elevation
where
![]() $A_1$ and
$A_1$ and ![]() $A_2$ are the real amplitudes of the two wave components;
$A_2$ are the real amplitudes of the two wave components; ![]() $A( x,t )$ is the slowly varying modulated complex amplitude;
$A( x,t )$ is the slowly varying modulated complex amplitude; ![]() $k$ and
$k$ and ![]() $\omega$ are the wavenumber and radian frequency of the short wave;
$\omega$ are the wavenumber and radian frequency of the short wave; ![]() $k_g$ and
$k_g$ and ![]() $\omega _g$ are the wavenumber and radian frequency of the wave group; and c.c. denotes the complex conjugate and will be omitted hereinafter. Assuming that the two wave frequencies are close to each other, substituting (2.3) into the equation of wave energy
$\omega _g$ are the wavenumber and radian frequency of the wave group; and c.c. denotes the complex conjugate and will be omitted hereinafter. Assuming that the two wave frequencies are close to each other, substituting (2.3) into the equation of wave energy
where ![]() $g$ is the gravitational acceleration and
$g$ is the gravitational acceleration and ![]() $\rho$ is the water density, gives
$\rho$ is the water density, gives
Equation (2.5) can be decomposed into a steady component and an unsteady oscillatory component. With the ![]() $\cos$ function expressed in complex form, the oscillatory wave energy is given by
$\cos$ function expressed in complex form, the oscillatory wave energy is given by
Assuming negligible breaking and bottom-friction-induced dissipation which may have a significant effect on wave radiation stress (Zou, Bowen & Hay Reference Zou, Bowen and Hay2006), the evolution of wave energy is governed by (see (2.6) in Mei & Benmoussa (Reference Mei and Benmoussa1984) and (2.4a) in Zou (Reference Zou2011))
and substituting (2.5) into (2.7), we have
where the subscript 0 denotes quantities at the incoming boundary of waves.
Substituting (2.6) into to (2.1) yields the oscillating component of the radiation stress:
where
Substituting (2.8b) into (2.10), we obtain
Following Reference Longuet-Higgins and StewartLHS62 (equations (3.33) and (3.34) therein), the 1-D linearised mass and momentum conservation equations for the subharmonic under the forcing of radiation stress are
where ![]() $\tilde {\xi }(x,t )$ and
$\tilde {\xi }(x,t )$ and ![]() $\tilde {M}( x,t )$ are the surface elevation and mass flux of the subharmonic, respectively, and
$\tilde {M}( x,t )$ are the surface elevation and mass flux of the subharmonic, respectively, and ![]() $h$ is the still water depth (see figure 1 for the definition of variables). Equations (2.12) and (2.13) are equivalent to the linearised equations (2.1) and (2.2) in Schäffer (Reference Schäffer1993). Eliminating
$h$ is the still water depth (see figure 1 for the definition of variables). Equations (2.12) and (2.13) are equivalent to the linearised equations (2.1) and (2.2) in Schäffer (Reference Schäffer1993). Eliminating ![]() $\tilde {M}$ in (2.12)–(2.13) yields
$\tilde {M}$ in (2.12)–(2.13) yields
 \begin{equation} \frac{{{\partial }^{2}}\tilde{\xi }}{\partial {{t}^{2}}}-g\frac{\partial }{\partial x}\left( h\frac{\partial \tilde{\xi }}{\partial x} \right)=\frac{1}{\rho }\frac{{{\partial }^{2}}\tilde{S}}{\partial {{x}^{2}}}. \end{equation}
\begin{equation} \frac{{{\partial }^{2}}\tilde{\xi }}{\partial {{t}^{2}}}-g\frac{\partial }{\partial x}\left( h\frac{\partial \tilde{\xi }}{\partial x} \right)=\frac{1}{\rho }\frac{{{\partial }^{2}}\tilde{S}}{\partial {{x}^{2}}}. \end{equation}Equation (2.14) is the governing equation of the surface elevation of group-induced subharmonics for 1-D wave groups propagating over a depth small compared with the wave group length (Longuet-Higgins & Stewart Reference Longuet-Higgins and Stewart1962). For non-breaking waves outside the surf zone, (2.9)–(2.11) are adopted, and (2.14) is consistent with the governing equation (2.11) in Mei & Benmoussa (Reference Mei and Benmoussa1984), equation (7) in Janssen et al. (Reference Janssen, Battjes and van Dongeren2003) and equation (2.7) in Zou (Reference Zou2011). For breaking waves in the surf zone, Symonds et al. (Reference Symonds, Huntley and Bowen1982) and Schäffer (Reference Schäffer1993) adopted the saturated breaking model assuming the wave height is proportional to local depth to model the forcing term and then solved equation (2.14), but no satisfactory verification against experiment has been reported. Using numerically modelled flow field to calculate the radiation stress, Rijnsdorp, Smit & Guza (Reference Rijnsdorp, Smit and Guza2022) showed that the linearised equation (2.14) remains adequate in the outer surf zone. Furthermore, Rijnsdorp et al. (Reference Rijnsdorp, Smit and Guza2022) demonstrated that the nonlinearity of infragravity wave itself starts to become important only in the inner surf zone over a mildly sloping beach of bottom slope 1/100. Liu et al. (Reference Liu, Yao, Liao, Li, Zhang and Zou2023) showed that fully nonlinear analysis of the infragravity wave energy budget is required for reef topography where the depth sharply reduces when offshore waves propagate over the foreslope into the reef flat.

Figure 1. Definition sketch of variables for wave groups propagating over variable bottom.
The group-induced subharmonic surface elevation ![]() $\tilde {\xi }( x,t )$ oscillates in time with the same frequency
$\tilde {\xi }( x,t )$ oscillates in time with the same frequency ![]() $\omega _g$ as the wave radiation stress
$\omega _g$ as the wave radiation stress ![]() $\tilde {S}$ in (2.9), i.e.
$\tilde {S}$ in (2.9), i.e.
where ![]() $\hat {\xi }$ is the complex amplitude of
$\hat {\xi }$ is the complex amplitude of ![]() $\tilde {\xi }( x,t )$. Substituting (2.9) and (2.15) into (2.14), we obtain the governing equation for the subharmonic complex amplitude
$\tilde {\xi }( x,t )$. Substituting (2.9) and (2.15) into (2.14), we obtain the governing equation for the subharmonic complex amplitude ![]() $\hat {\xi }(x)$:
$\hat {\xi }(x)$:
 \begin{equation} \frac{1}{h}\frac{\rm d}{{\rm d}\,x}\left( h\frac{{\rm d}\hat{\xi }}{{\rm d}\,x} \right)+k_{f}^{2}\hat{\xi }={-}\frac{1}{\rho gh}\frac{{{\rm d}^{2}}\hat{S}}{{\rm d}\,{{x}^{2}}}, \end{equation}
\begin{equation} \frac{1}{h}\frac{\rm d}{{\rm d}\,x}\left( h\frac{{\rm d}\hat{\xi }}{{\rm d}\,x} \right)+k_{f}^{2}\hat{\xi }={-}\frac{1}{\rho gh}\frac{{{\rm d}^{2}}\hat{S}}{{\rm d}\,{{x}^{2}}}, \end{equation}
where ![]() $k_f=\omega _g / \sqrt {gh}$ is the wavenumber of free subharmonics propagating at the speed of shallow-water wave. Equation (2.16) is consistent with the governing equation (4.9) in Schäffer (Reference Schäffer1993), equation (10) in Janssen et al. (Reference Janssen, Battjes and van Dongeren2003) and equation (3.4) in Zou (Reference Zou2011). A novel unified solution to (2.16) is developed based on Green's function in the present study.
$k_f=\omega _g / \sqrt {gh}$ is the wavenumber of free subharmonics propagating at the speed of shallow-water wave. Equation (2.16) is consistent with the governing equation (4.9) in Schäffer (Reference Schäffer1993), equation (10) in Janssen et al. (Reference Janssen, Battjes and van Dongeren2003) and equation (3.4) in Zou (Reference Zou2011). A novel unified solution to (2.16) is developed based on Green's function in the present study.
3. Unified solution based on Green's function
3.1. General form of solution
The Green's function ![]() $G(x,y)$ of a 1-D linear differential equation describes the response at
$G(x,y)$ of a 1-D linear differential equation describes the response at ![]() $x$ to a unit forcing at
$x$ to a unit forcing at ![]() $y$, where
$y$, where ![]() $x$ and
$x$ and ![]() $y$ denote two spatial coordinates in 1-D space. Assuming a continuously varying water depth
$y$ denote two spatial coordinates in 1-D space. Assuming a continuously varying water depth ![]() $h(x)$, the governing equation (2.16) becomes a Sturm–Liouville type equation. The corresponding Green's function satisfies (see equations (3.3.6), (3.3.9) and (3.3.10) in Duffy Reference Duffy2015) the following equations:
$h(x)$, the governing equation (2.16) becomes a Sturm–Liouville type equation. The corresponding Green's function satisfies (see equations (3.3.6), (3.3.9) and (3.3.10) in Duffy Reference Duffy2015) the following equations:
where ![]() $\delta _{Dirac}(x-y )$ is the Dirac Delta function that physically describes the unit point forcing oscillating at the wave group frequency at
$\delta _{Dirac}(x-y )$ is the Dirac Delta function that physically describes the unit point forcing oscillating at the wave group frequency at ![]() $x'=x-y=0$ and satisfies
$x'=x-y=0$ and satisfies ![]() $\delta _{Dirac}(x') = 0$ for
$\delta _{Dirac}(x') = 0$ for ![]() $x'\neq 0$ and
$x'\neq 0$ and ![]() $\int _{-\infty }^{+\infty }\delta _{Dirac}(x')\,\mathrm {d}\,x'=1$. An example of
$\int _{-\infty }^{+\infty }\delta _{Dirac}(x')\,\mathrm {d}\,x'=1$. An example of ![]() $G(x,y)$ over a flat bottom is later shown in figure 3.
$G(x,y)$ over a flat bottom is later shown in figure 3.
Let ![]() $\hat {f}(x )$ be the complex amplitude of the forcing term of (2.16), i.e.
$\hat {f}(x )$ be the complex amplitude of the forcing term of (2.16), i.e.
For any given response position ![]() $x$, we can always find a subdomain
$x$, we can always find a subdomain ![]() $a < x < b$ where the equality
$a < x < b$ where the equality
is valid.
Applying the multiplication and then integration on the right-hand side of (3.3) to both sides of (3.1a) and comparing with the governing equation of subharmonic complex amplitude (2.16), the inhomogeneous solution ![]() $\hat \xi _g(x)$ to (2.16) is found in the form of
$\hat \xi _g(x)$ to (2.16) is found in the form of
which physically describes the group-induced subharmonic at ![]() $x$ as the linear superposition of the responses at
$x$ as the linear superposition of the responses at ![]() $x$ induced by all the wave group forcing
$x$ induced by all the wave group forcing ![]() $\hat f(\kern0.7pt y )$ distributed in the domain
$\hat f(\kern0.7pt y )$ distributed in the domain ![]() $a< y< b$. The generalised solution to (2.16) can be constructed as the sum of homogeneous and inhomogeneous components (cf. Ince Reference Ince1956, § XI):
$a< y< b$. The generalised solution to (2.16) can be constructed as the sum of homogeneous and inhomogeneous components (cf. Ince Reference Ince1956, § XI):
where the homogeneous solution ![]() ${\hat \xi _f}( x )$ denotes the free infragravity wave that satisfies the homogeneous counterpart of governing equation (2.16). Physically, the response to each point forcing
${\hat \xi _f}( x )$ denotes the free infragravity wave that satisfies the homogeneous counterpart of governing equation (2.16). Physically, the response to each point forcing ![]() $\hat f(\kern0.7pt y )$ over
$\hat f(\kern0.7pt y )$ over ![]() $a< y< b$ propagates away from the source point
$a< y< b$ propagates away from the source point ![]() $x = y$ as free subharmonics (figure 2), because (3.1a) indicates that
$x = y$ as free subharmonics (figure 2), because (3.1a) indicates that ![]() $G( {x,y} )$ is the homogeneous solution to (2.16) at all
$G( {x,y} )$ is the homogeneous solution to (2.16) at all ![]() $x$ in the domain except for
$x$ in the domain except for ![]() $x = y$. Therefore, (3.4) shows that the group-induced subharmonic at an observation point
$x = y$. Therefore, (3.4) shows that the group-induced subharmonic at an observation point ![]() $x$ is the linear superposition of free subharmonics generated from all source points
$x$ is the linear superposition of free subharmonics generated from all source points ![]() $x = y$ in the wave field due to local group forcing. Note that, at the observation position
$x = y$ in the wave field due to local group forcing. Note that, at the observation position ![]() $x$ within this domain, the response to group forcing outside this domain appears as ambient free subharmonic
$x$ within this domain, the response to group forcing outside this domain appears as ambient free subharmonic ![]() ${\hat \xi _f}$ in solution (3.5).
${\hat \xi _f}$ in solution (3.5).

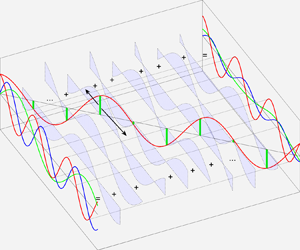
Figure 2. Diagram of two downwave-propagating (red) and upwave-propagating (blue) free subharmonics emitted from an arbitrary spatial point ![]() $x=y$ in the source field
$x=y$ in the source field ![]() $\hat \sigma (\kern0.7pt y )$ (3.7) due to group forcing. The source field
$\hat \sigma (\kern0.7pt y )$ (3.7) due to group forcing. The source field ![]() $\hat \sigma (\kern0.7pt y )$ due to the forcing of radiation stress varies at the spatial scale of wave group length (see (3.22) for an example). The superposition of all the free subharmonics emitted everywhere yields the group-induced subharmonic.
$\hat \sigma (\kern0.7pt y )$ due to the forcing of radiation stress varies at the spatial scale of wave group length (see (3.22) for an example). The superposition of all the free subharmonics emitted everywhere yields the group-induced subharmonic.
Equation (3.4) may be rewritten as
The initial complex amplitude of each emitted subharmonic generated per unit distance is ![]() $\hat f(\kern0.7pt y )G(\kern0.7pt {y,y} )$, whose spatial variation from
$\hat f(\kern0.7pt y )G(\kern0.7pt {y,y} )$, whose spatial variation from ![]() $y$ to
$y$ to ![]() $x$ is described by
$x$ is described by ![]() $G( {x,y} ) / G(\kern0.7pt {y,y} )$ (figure 2). Accordingly,
$G( {x,y} ) / G(\kern0.7pt {y,y} )$ (figure 2). Accordingly, ![]() $\hat f(\kern0.7pt y )G(\kern0.7pt {y,y} )$ is defined as the source field of the group-induced subharmonic
$\hat f(\kern0.7pt y )G(\kern0.7pt {y,y} )$ is defined as the source field of the group-induced subharmonic ![]() $\hat \sigma (\kern0.7pt y )$, i.e.
$\hat \sigma (\kern0.7pt y )$, i.e.
Let ![]() $\hat \xi _h^+ ( x )$ and
$\hat \xi _h^+ ( x )$ and ![]() $\hat \xi _h^- ( x )$ be the linearly independent homogeneous solutions of (2.16) that describe the downwave- and upwave-propagating free subharmonics, respectively. The Green's function that satisfies (3.1) can be constructed using two distinct linear combinations of
$\hat \xi _h^- ( x )$ be the linearly independent homogeneous solutions of (2.16) that describe the downwave- and upwave-propagating free subharmonics, respectively. The Green's function that satisfies (3.1) can be constructed using two distinct linear combinations of ![]() $\hat \xi _h^+ ( x )$ and
$\hat \xi _h^+ ( x )$ and ![]() $\hat \xi _h^- ( x )$ (see Ince Reference Ince1956, p. 257). Assuming open boundaries at both
$\hat \xi _h^- ( x )$ (see Ince Reference Ince1956, p. 257). Assuming open boundaries at both ![]() $x=a$ and
$x=a$ and ![]() $x=b$, we seek a solution of
$x=b$, we seek a solution of ![]() $G(x,y)$ that satisfies the following boundary condition:
$G(x,y)$ that satisfies the following boundary condition:
 \begin{equation} \frac{G(b,y)}{G(\kern0.7pt y,y)} = \frac{\hat \xi _h^+ \left( b \right)}{\hat \xi _h^+ \left(\kern0.7pt y \right)},\quad \frac{G(a,y)}{G(\kern0.7pt y,y)} = \frac{\hat \xi _h^- \left( a \right)}{\hat \xi _h^- \left(\kern0.7pt y \right)}, \end{equation}
\begin{equation} \frac{G(b,y)}{G(\kern0.7pt y,y)} = \frac{\hat \xi _h^+ \left( b \right)}{\hat \xi _h^+ \left(\kern0.7pt y \right)},\quad \frac{G(a,y)}{G(\kern0.7pt y,y)} = \frac{\hat \xi _h^- \left( a \right)}{\hat \xi _h^- \left(\kern0.7pt y \right)}, \end{equation}
which physically indicates that the local response generated at source location ![]() $y$ arrives at boundary
$y$ arrives at boundary ![]() $x=a$ and
$x=a$ and ![]() $x=b$ as an upwave- and downwave-propagating free wave so that the spatial evolution of its complex amplitude is described by
$x=b$ as an upwave- and downwave-propagating free wave so that the spatial evolution of its complex amplitude is described by ![]() $\hat \xi _h^+$ or
$\hat \xi _h^+$ or ![]() $\hat \xi _h^-$.
$\hat \xi _h^-$.
The solution for the governing equation (3.1) and the boundary condition (3.8a,b) is given by
 \begin{equation}
G\left(x,y\right) = \left\{ \begin{array}{@{}ll@{}} G\left(\kern0.7pt y,y \right)\dfrac{\hat{\xi }_{h}^{+}\left( x
\right)}{\hat{\xi }_{h}^{+}\left(\kern0.7pt y \right)}, & \text{ for }x>y,\\
G\left(\kern0.7pt y,y \right)\dfrac{\hat{\xi }_{h}^{-}\left(
x \right)}{\hat{\xi }_{h}^{-}\left(\kern0.7pt y \right)}, & \text{
for }x< y, \end{array} \right.
\end{equation}
\begin{equation}
G\left(x,y\right) = \left\{ \begin{array}{@{}ll@{}} G\left(\kern0.7pt y,y \right)\dfrac{\hat{\xi }_{h}^{+}\left( x
\right)}{\hat{\xi }_{h}^{+}\left(\kern0.7pt y \right)}, & \text{ for }x>y,\\
G\left(\kern0.7pt y,y \right)\dfrac{\hat{\xi }_{h}^{-}\left(
x \right)}{\hat{\xi }_{h}^{-}\left(\kern0.7pt y \right)}, & \text{
for }x< y, \end{array} \right.
\end{equation}with
 \begin{equation} G\left(\kern0.7pt {y,y} \right) = {\left. {\dfrac{{\hat \xi _h^+ \hat \xi _h^- }}{{\hat \xi _h^- \dfrac{\rm d}{{{\rm d}\,x}}\hat \xi _h^+{-} \hat \xi _h^+ \dfrac{\rm d}{{{\rm d}\,x}}\hat \xi _h^- }}} \right|_{x = y}}, \end{equation}
\begin{equation} G\left(\kern0.7pt {y,y} \right) = {\left. {\dfrac{{\hat \xi _h^+ \hat \xi _h^- }}{{\hat \xi _h^- \dfrac{\rm d}{{{\rm d}\,x}}\hat \xi _h^+{-} \hat \xi _h^+ \dfrac{\rm d}{{{\rm d}\,x}}\hat \xi _h^- }}} \right|_{x = y}}, \end{equation}
where the denominator of (3.10) is the Wronskian of ![]() $\hat \xi _h^-$ and
$\hat \xi _h^-$ and ![]() $\hat \xi _h^+$, and it is non-zero owing to the linear independence between
$\hat \xi _h^+$, and it is non-zero owing to the linear independence between ![]() $\hat \xi _h^+$ and
$\hat \xi _h^+$ and ![]() $\hat \xi _h^-$.
$\hat \xi _h^-$.
In (3.9), the Green's function at the source point ![]() $x = y$,
$x = y$, ![]() $G(\kern0.7pt {y,y} )$, represents the initial complex amplitude of the subharmonic generated by the local unit point forcing, while the factor
$G(\kern0.7pt {y,y} )$, represents the initial complex amplitude of the subharmonic generated by the local unit point forcing, while the factor ![]() $\hat \xi _h^ \pm (x)/\hat \xi _h^ \pm (\kern0.7pt y ) = G(x,y)/G(\kern0.7pt y,y)$ describes the relative changes in amplitude and phase of
$\hat \xi _h^ \pm (x)/\hat \xi _h^ \pm (\kern0.7pt y ) = G(x,y)/G(\kern0.7pt y,y)$ describes the relative changes in amplitude and phase of ![]() $G(x,y)$ from
$G(x,y)$ from ![]() $x=y$ to
$x=y$ to ![]() $x=x$.
$x=x$.
Substituting (3.9) into (3.6), and recalling the definition of the source field ![]() $\hat \sigma (\kern0.7pt y )$ (3.7), yields
$\hat \sigma (\kern0.7pt y )$ (3.7), yields
where
 \begin{equation} \hat \xi _g^+ \left( x \right) = \int_a^x {\hat \sigma \left(\kern0.7pt y \right)\dfrac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y} ,\quad \hat \xi _g^- \left( x \right) = \int_x^b {\hat \sigma \left(\kern0.7pt y \right)\dfrac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^- \left(\kern0.7pt y \right)}}\,\mathrm{d} y}. \end{equation}
\begin{equation} \hat \xi _g^+ \left( x \right) = \int_a^x {\hat \sigma \left(\kern0.7pt y \right)\dfrac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y} ,\quad \hat \xi _g^- \left( x \right) = \int_x^b {\hat \sigma \left(\kern0.7pt y \right)\dfrac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^- \left(\kern0.7pt y \right)}}\,\mathrm{d} y}. \end{equation}
The superscripts ![]() $+$ and
$+$ and ![]() $-$ denote the two components that form due to the downwave- and upwave-propagating free subharmonics being generated on the upwave and downwave sides of
$-$ denote the two components that form due to the downwave- and upwave-propagating free subharmonics being generated on the upwave and downwave sides of ![]() $x$, respectively.
$x$, respectively.
Given the complex amplitudes of the ambient downwave- and upwave-propagating subharmonics at the boundary, i.e. ![]() $\hat \xi _f^+ ( a )$ and
$\hat \xi _f^+ ( a )$ and ![]() $\hat \xi _f^- ( b )$, the ambient free subharmonic in the domain
$\hat \xi _f^- ( b )$, the ambient free subharmonic in the domain ![]() $a< x< b$ can be expressed as
$a< x< b$ can be expressed as
where
 \begin{equation} \hat \xi _f^+ \left( x \right) = \hat \xi _f^+ \left( a \right)\dfrac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left( a \right)}},\quad \hat \xi _f^- \left( x \right) = \hat \xi _f^- \left( b \right)\dfrac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^- \left( b \right)}} \end{equation}
\begin{equation} \hat \xi _f^+ \left( x \right) = \hat \xi _f^+ \left( a \right)\dfrac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left( a \right)}},\quad \hat \xi _f^- \left( x \right) = \hat \xi _f^- \left( b \right)\dfrac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^- \left( b \right)}} \end{equation}
describe the downwave- and upwave-propagating components, respectively. Note that ![]() $\hat \xi _f^ \pm (x)$ differs from
$\hat \xi _f^ \pm (x)$ differs from ![]() $\hat \xi _h^ \pm (x)$ in that the former's boundary values vary with the boundary locations in the manner of a group-induced subharmonic instead of a free subharmonic, in order to incorporate the contribution of the source field in the incremental domain due to changing boundary locations. This is later demonstrated by the relationship between
$\hat \xi _h^ \pm (x)$ in that the former's boundary values vary with the boundary locations in the manner of a group-induced subharmonic instead of a free subharmonic, in order to incorporate the contribution of the source field in the incremental domain due to changing boundary locations. This is later demonstrated by the relationship between ![]() $\hat \xi _f^-(a)$ and
$\hat \xi _f^-(a)$ and ![]() $\hat \xi _f^-(b)$ in (3.17).
$\hat \xi _f^-(b)$ in (3.17).
Substituting (3.11)–(3.14a,b) into (3.5) yields
 \begin{align} \hat \xi \left( x \right) = \int_a^x {\hat \sigma \left(\kern0.7pt y \right)\frac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y} + \hat \xi _f^+ \left( a \right)\frac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left( a \right)}} + \int_x^b {\hat \sigma \left(\kern0.7pt y \right)\frac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^- \left(\kern0.7pt y \right)}}\,\mathrm{d} y} + \hat \xi _f^- \left( b \right)\frac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^- \left( b \right)}}. \end{align}
\begin{align} \hat \xi \left( x \right) = \int_a^x {\hat \sigma \left(\kern0.7pt y \right)\frac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y} + \hat \xi _f^+ \left( a \right)\frac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left( a \right)}} + \int_x^b {\hat \sigma \left(\kern0.7pt y \right)\frac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^- \left(\kern0.7pt y \right)}}\,\mathrm{d} y} + \hat \xi _f^- \left( b \right)\frac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^- \left( b \right)}}. \end{align}
Equation (3.15) is the general form of the solution to (2.16), and its exact form depends on the expression of the wave radiation stress field and homogeneous solution. However, the solution in the form of (3.15) requires the information at two boundaries on both sides of ![]() $x$. To facilitate its practical applications, (3.15) can be rewritten as a solution with only one boundary for integration retained:
$x$. To facilitate its practical applications, (3.15) can be rewritten as a solution with only one boundary for integration retained:
 \begin{align} \hat \xi
\left( x \right) & = \int_a^x {\hat \sigma \left(\kern0.7pt y \right)\frac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi
_h^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y} + \hat \xi _f^+
\left( a \right)\frac{{\hat \xi _h^+ \left( x
\right)}}{{\hat \xi _h^+ \left( a \right)}} \nonumber\\
&\quad+ \int_x^a {\hat \sigma \left(\kern0.7pt y \right)\frac{{\hat
\xi _h^- \left( x \right)}}{{\hat \xi _h^- \left(\kern0.7pt y \right)}}\,\mathrm{d} y} + \int_a^b {\hat \sigma \left(\kern0.7pt y \right)\frac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi
_h^- \left(\kern0.7pt y \right)}}\,\mathrm{d} y} + \hat \xi _f^-
\left( b \right)\frac{{\hat \xi _h^- \left( x
\right)}}{{\hat \xi _h^- \left( b \right)}} \nonumber\\
& = \hat \xi _f^+ \left( a \right)\frac{{\hat \xi _h^+ \left( x
\right)}}{{\hat \xi _h^+ \left( a \right)}} + \hat \xi _f^-
\left( a \right)\frac{{\hat \xi _h^- \left( x
\right)}}{{\hat \xi _h^- \left( a \right)}} + \int_a^x
{\hat \sigma \left(\kern0.7pt y \right)\left[\frac{{\hat \xi _h^+
\left( x \right)}}{{\hat \xi _h^+ \left(\kern0.7pt y \right)}} -
\frac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^-
\left(\kern0.7pt y \right)}}\right]\,\mathrm{d} y},
\end{align}
\begin{align} \hat \xi
\left( x \right) & = \int_a^x {\hat \sigma \left(\kern0.7pt y \right)\frac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi
_h^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y} + \hat \xi _f^+
\left( a \right)\frac{{\hat \xi _h^+ \left( x
\right)}}{{\hat \xi _h^+ \left( a \right)}} \nonumber\\
&\quad+ \int_x^a {\hat \sigma \left(\kern0.7pt y \right)\frac{{\hat
\xi _h^- \left( x \right)}}{{\hat \xi _h^- \left(\kern0.7pt y \right)}}\,\mathrm{d} y} + \int_a^b {\hat \sigma \left(\kern0.7pt y \right)\frac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi
_h^- \left(\kern0.7pt y \right)}}\,\mathrm{d} y} + \hat \xi _f^-
\left( b \right)\frac{{\hat \xi _h^- \left( x
\right)}}{{\hat \xi _h^- \left( b \right)}} \nonumber\\
& = \hat \xi _f^+ \left( a \right)\frac{{\hat \xi _h^+ \left( x
\right)}}{{\hat \xi _h^+ \left( a \right)}} + \hat \xi _f^-
\left( a \right)\frac{{\hat \xi _h^- \left( x
\right)}}{{\hat \xi _h^- \left( a \right)}} + \int_a^x
{\hat \sigma \left(\kern0.7pt y \right)\left[\frac{{\hat \xi _h^+
\left( x \right)}}{{\hat \xi _h^+ \left(\kern0.7pt y \right)}} -
\frac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^-
\left(\kern0.7pt y \right)}}\right]\,\mathrm{d} y},
\end{align}where
 \begin{equation} \hat \xi _f^- \left( a \right) = \hat \xi _f^- \left( b \right)\frac{{\hat \xi _h^- \left( a \right)}}{{\hat \xi _h^- \left( b \right)}} + \int_a^b {\hat \sigma \left(\kern0.7pt y \right)\frac{{\hat \xi _h^- \left( a \right)}}{{\hat \xi _h^- \left(\kern0.7pt y \right)}}\,\mathrm{d} y} \end{equation}
\begin{equation} \hat \xi _f^- \left( a \right) = \hat \xi _f^- \left( b \right)\frac{{\hat \xi _h^- \left( a \right)}}{{\hat \xi _h^- \left( b \right)}} + \int_a^b {\hat \sigma \left(\kern0.7pt y \right)\frac{{\hat \xi _h^- \left( a \right)}}{{\hat \xi _h^- \left(\kern0.7pt y \right)}}\,\mathrm{d} y} \end{equation}
is the complex amplitude of upwave-propagating free wave at ![]() $x=a$, which includes the contributions of free waves entering the region through the right-hand boundary
$x=a$, which includes the contributions of free waves entering the region through the right-hand boundary ![]() $x=b$ and those generated due to the group forcing in the region
$x=b$ and those generated due to the group forcing in the region ![]() $a< x< b$. The solution in the form of (3.16) is more computationally feasible than (3.15) and is used for the calculation in figure 6, but the former is physically not as intuitive as the latter because the effect of group forcing on the upwave-propagating components is manifested by deducting the contribution of sources along integral path from the overall contributions of sources.
$a< x< b$. The solution in the form of (3.16) is more computationally feasible than (3.15) and is used for the calculation in figure 6, but the former is physically not as intuitive as the latter because the effect of group forcing on the upwave-propagating components is manifested by deducting the contribution of sources along integral path from the overall contributions of sources.
3.2. Flat bottom
Over a flat bottom, the governing equation (2.16) reduces to
where the forcing term ![]() $\hat f$ is given by (3.2). According to (2.10)–(2.11), over a flat bottom
$\hat f$ is given by (3.2). According to (2.10)–(2.11), over a flat bottom ![]() $\hat f$ may be rewritten as
$\hat f$ may be rewritten as
which is in phase with the wave group. In addition, over a flat bottom, the homogeneous solutions to the governing equation (2.16) and thus the local response to unit point forcing described in equation (3.10) are given by
where ![]() $C^{\pm }$ is a non-zero constant.
$C^{\pm }$ is a non-zero constant.
Substituting (3.20a,b) into (3.9), we derive the Green's function for a flat bottom:
where the variation of ![]() $G(x,y)$ with source location
$G(x,y)$ with source location ![]() $y$ and response location
$y$ and response location ![]() $x$ is shown in figure 3. For a point unit forcing at
$x$ is shown in figure 3. For a point unit forcing at ![]() $x=y$ described by
$x=y$ described by ![]() $\delta _{Dirac}(x-y) {\rm e}^{-\mathrm {i}\omega _g t}$, the modulus and phase angle of
$\delta _{Dirac}(x-y) {\rm e}^{-\mathrm {i}\omega _g t}$, the modulus and phase angle of ![]() $G(x,y)$ are the amplitude and phase lag with respect to the forcing of the subharmonic at
$G(x,y)$ are the amplitude and phase lag with respect to the forcing of the subharmonic at ![]() $x$. The gradient of the real part of
$x$. The gradient of the real part of ![]() $G(x,y)$ is not continuous as the right-hand side of (3.1c) is real.
$G(x,y)$ is not continuous as the right-hand side of (3.1c) is real.

Figure 3. (a) Real and (b) imaginary parts of the normalised Green's function for a flat bottom (3.21).
Substituting (3.19) and (3.20b) into the source field ![]() $\hat \sigma (\kern0.7pt y )= \hat f(\kern0.7pt y )G(\kern0.7pt {y,y} )$, we have
$\hat \sigma (\kern0.7pt y )= \hat f(\kern0.7pt y )G(\kern0.7pt {y,y} )$, we have
which is spatially uniform in amplitude and leads the wave group by ![]() ${\rm \pi} /2$ in phase as
${\rm \pi} /2$ in phase as ![]() $\hat S(a){\rm e}^{\mathrm {i}k_g(\kern0.7pt y - a)}$ is in phase with the wave group according to (2.10) and the phase of the complex factor
$\hat S(a){\rm e}^{\mathrm {i}k_g(\kern0.7pt y - a)}$ is in phase with the wave group according to (2.10) and the phase of the complex factor ![]() $\mathrm {i}^{-1}$ is
$\mathrm {i}^{-1}$ is ![]() $-{\rm \pi} /2$. Equation (3.22) indicates that each free subharmonic emitted from the source field has the same amplitude and is initially in quadrature with the wave group.
$-{\rm \pi} /2$. Equation (3.22) indicates that each free subharmonic emitted from the source field has the same amplitude and is initially in quadrature with the wave group.
Substituting (3.20a) into (3.11)–(3.12a,b) yields the solution for ![]() $\hat \xi _g$:
$\hat \xi _g$:
Invoking (3.22) further yields the expressions
 \begin{align} \hat \xi_g(x) &=
\frac{\hat{f}(0)}{2 \mathrm{i} k_f} \int_{a}^{b}\ {\rm e}^{\mathrm{i}{(k_g y + k_f|x-y|)}}\,
\mathrm{d} y \nonumber\\ & =
\frac{{k_g^2}}{{2\mathrm{i}{k_f}}}\frac{{\hat S\left( a
\right)}}{{\rho gh}} {\rm e}^{-\mathrm{i}{k_g a}}
\int_{a}^{b}\ {\rm e}^{\mathrm{i}{(k_g y + k_f|x-y|)}}\, \mathrm{d} y.
\end{align}
\begin{align} \hat \xi_g(x) &=
\frac{\hat{f}(0)}{2 \mathrm{i} k_f} \int_{a}^{b}\ {\rm e}^{\mathrm{i}{(k_g y + k_f|x-y|)}}\,
\mathrm{d} y \nonumber\\ & =
\frac{{k_g^2}}{{2\mathrm{i}{k_f}}}\frac{{\hat S\left( a
\right)}}{{\rho gh}} {\rm e}^{-\mathrm{i}{k_g a}}
\int_{a}^{b}\ {\rm e}^{\mathrm{i}{(k_g y + k_f|x-y|)}}\, \mathrm{d} y.
\end{align}
Taking the integral in (3.23b) over the upwave side of ![]() $x$ (
$x$ (![]() $a< y< x$) yields the solution for
$a< y< x$) yields the solution for ![]() $\hat \xi _g^+$ as defined in (3.12a):
$\hat \xi _g^+$ as defined in (3.12a):
 \begin{align} \hat \xi _g^+ \left( x
\right) & = \frac{{k_g^2}}{{2\mathrm{i}{k_f}}}\frac{{\hat
S\left( a \right)}}{{\rho gh}} {\rm e}^{-\mathrm{i}{k_g a}}
\int_{a}^{x}\ {\rm e}^{\mathrm{i}{[k_g y + k_f(x-y)]}} \,\mathrm{d} y\nonumber\\ & =
\frac{k_g^2}{2\mathrm{i}k_f}\frac{\hat{S}(a)}{\rho g h}
{\rm e}^{\mathrm{i}(k_f x-k_g a)} \int_a^x {\rm
e}^{\mathrm{i}(k_g -k_f)y}\,\mathrm{d} y\nonumber\\ & ={-}
\frac{k_g^2}{2k_f} \frac{\hat{S}(x) - \hat{S}(a){\rm
e}^{\mathrm{i}k_f(x-a)}}{{\rho g h}(k_g - k_f)},
\end{align}
\begin{align} \hat \xi _g^+ \left( x
\right) & = \frac{{k_g^2}}{{2\mathrm{i}{k_f}}}\frac{{\hat
S\left( a \right)}}{{\rho gh}} {\rm e}^{-\mathrm{i}{k_g a}}
\int_{a}^{x}\ {\rm e}^{\mathrm{i}{[k_g y + k_f(x-y)]}} \,\mathrm{d} y\nonumber\\ & =
\frac{k_g^2}{2\mathrm{i}k_f}\frac{\hat{S}(a)}{\rho g h}
{\rm e}^{\mathrm{i}(k_f x-k_g a)} \int_a^x {\rm
e}^{\mathrm{i}(k_g -k_f)y}\,\mathrm{d} y\nonumber\\ & ={-}
\frac{k_g^2}{2k_f} \frac{\hat{S}(x) - \hat{S}(a){\rm
e}^{\mathrm{i}k_f(x-a)}}{{\rho g h}(k_g - k_f)},
\end{align}
where the relationship ![]() $\hat {S}(x) = \hat {S}(a){\rm e}^{\mathrm {i}k_g(x-a)}$ is used. Similarly, the solution for
$\hat {S}(x) = \hat {S}(a){\rm e}^{\mathrm {i}k_g(x-a)}$ is used. Similarly, the solution for ![]() $\hat \xi _g^-$ is derived by integrating over the downwave side
$\hat \xi _g^-$ is derived by integrating over the downwave side ![]() $x< y< b$ as
$x< y< b$ as
where the relationship ![]() $\hat {S}(x) = \hat {S}(b){\rm e}^{\mathrm {i}k_g(x-b)}$ is used. Let
$\hat {S}(x) = \hat {S}(b){\rm e}^{\mathrm {i}k_g(x-b)}$ is used. Let ![]() $\hat \xi _b^+$ and
$\hat \xi _b^+$ and ![]() $\hat \xi _b^-$ be the corresponding components bound to
$\hat \xi _b^-$ be the corresponding components bound to ![]() $\hat S(x)$ and therefore wave group in (3.24) and (3.25), i.e.
$\hat S(x)$ and therefore wave group in (3.24) and (3.25), i.e.
Equations (3.24) and (3.25) can be rewritten as
 \begin{equation} \left. \begin{aligned} \hat \xi _g^+ \left( x \right) & = \hat \xi _b^+ \left( x \right) - \hat \xi _b^+ \left( a \right) {{\rm e}^{\mathrm{i}{k_f}\left( {x - a} \right)}},\\ \hat \xi _g^- \left( x \right) & = \hat \xi _b^- \left( x \right) - \hat \xi _b^- \left( b \right){{\rm e}^{ - \mathrm{i}{k_f}\left( {x - b} \right)}}. \end{aligned} \right\} \end{equation}
\begin{equation} \left. \begin{aligned} \hat \xi _g^+ \left( x \right) & = \hat \xi _b^+ \left( x \right) - \hat \xi _b^+ \left( a \right) {{\rm e}^{\mathrm{i}{k_f}\left( {x - a} \right)}},\\ \hat \xi _g^- \left( x \right) & = \hat \xi _b^- \left( x \right) - \hat \xi _b^- \left( b \right){{\rm e}^{ - \mathrm{i}{k_f}\left( {x - b} \right)}}. \end{aligned} \right\} \end{equation}3.2.1. Intermediate water
In intermediate water, ![]() ${c_g} < \sqrt {gh}$ and
${c_g} < \sqrt {gh}$ and ![]() ${k_g} > {k_f}$. Figure 4(a) shows the spatial variation of the phase of all subharmonics emitted for the source location
${k_g} > {k_f}$. Figure 4(a) shows the spatial variation of the phase of all subharmonics emitted for the source location ![]() $y$ and the observation position
$y$ and the observation position ![]() $x$, as described by
$x$, as described by ![]() $\exp [\mathrm {i}(k_g y + k_f | x - y |) ]$ (the integrand in (3.23b)). On the one hand, at each given
$\exp [\mathrm {i}(k_g y + k_f | x - y |) ]$ (the integrand in (3.23b)). On the one hand, at each given ![]() $y$, the horizontal slice of figure 4(a) describes the phase change of the upwave- and downwave-propagating subharmonics emitted from
$y$, the horizontal slice of figure 4(a) describes the phase change of the upwave- and downwave-propagating subharmonics emitted from ![]() $x=y$, resembling the picture shown in figure 2. On the other hand, at each given
$x=y$, resembling the picture shown in figure 2. On the other hand, at each given ![]() $x$, the vertical slice of figure 4(a) describes the phase variation with the source location
$x$, the vertical slice of figure 4(a) describes the phase variation with the source location ![]() $y$ of all subharmonics arriving at
$y$ of all subharmonics arriving at ![]() $x$. Figure 4(b,c) shows that the superposition of all free subharmonics can be further decomposed into a subharmonic bound to the wave group and a free subharmonic which are respectively described by the first and second terms on the right-hand side of (3.27).
$x$. Figure 4(b,c) shows that the superposition of all free subharmonics can be further decomposed into a subharmonic bound to the wave group and a free subharmonic which are respectively described by the first and second terms on the right-hand side of (3.27).

Figure 4. Diagram of the emission, propagation and interference of subharmonics generated from the source field ![]() $\hat \sigma (\kern0.7pt y ) = \hat f (\kern0.7pt y )G(\kern0.7pt {y,y} )$ due to group forcing of bichromatic waves over a flat bottom in intermediate depth (
$\hat \sigma (\kern0.7pt y ) = \hat f (\kern0.7pt y )G(\kern0.7pt {y,y} )$ due to group forcing of bichromatic waves over a flat bottom in intermediate depth (![]() ${k_g} > {k_f}$, where
${k_g} > {k_f}$, where ![]() $k_g=\omega _g/c_g$ and
$k_g=\omega _g/c_g$ and ![]() $k_f= \omega _g / \sqrt {gh}$ are the wavenumbers of wave group and free subharmonic propagating as shallow-water wave, respectively). Here
$k_f= \omega _g / \sqrt {gh}$ are the wavenumbers of wave group and free subharmonic propagating as shallow-water wave, respectively). Here ![]() $\hat {f}$ is the forcing term and
$\hat {f}$ is the forcing term and ![]() $G(\kern0.7pt y,y)$ is the Green's function at
$G(\kern0.7pt y,y)$ is the Green's function at ![]() $x=y$. (a) Term
$x=y$. (a) Term ![]() $\exp [\mathrm {i}(k_g y + k_f | x - y |) ]$ gives the spatial variation of product of source field and Green's function as shown in (3.23), which in turn describe the spatial variation of the free subharmonic with its source position
$\exp [\mathrm {i}(k_g y + k_f | x - y |) ]$ gives the spatial variation of product of source field and Green's function as shown in (3.23), which in turn describe the spatial variation of the free subharmonic with its source position ![]() $y$ and observation position
$y$ and observation position ![]() $x$. The vertical and horizontal white arrows denote the wavenumber of each emitted subharmonic component on the source and observation position, respectively. (b) The
$x$. The vertical and horizontal white arrows denote the wavenumber of each emitted subharmonic component on the source and observation position, respectively. (b) The ![]() $y$ axis denotes the real part of the superposed downwave-propagating subharmonic (
$y$ axis denotes the real part of the superposed downwave-propagating subharmonic (![]() $\hat \xi _g^+$, (3.24)), showing the surface elevation snapshot for
$\hat \xi _g^+$, (3.24)), showing the surface elevation snapshot for ![]() $t = 0$. (c) Similar to (b) but for the upwave component (
$t = 0$. (c) Similar to (b) but for the upwave component (![]() $\hat \xi _g^-$, (3.25)).
$\hat \xi _g^-$, (3.25)).
The emergence of a bound subharmonic from the superposition of all free subharmonics is essentially the consequence of wave-group-modulated emission of each free subharmonic through the source field bound to the wave group, which does not conflict with the interpretation of the group-induced subharmonic as the superposition of free subharmonics. More specifically, the modulated emission means the phase of the source field by (3.22) varies with space as ![]() $k_g y$ due to direct modulation of group forcing, indicating that free subharmonics with the same initial phase are generated at equidistant locations separated by
$k_g y$ due to direct modulation of group forcing, indicating that free subharmonics with the same initial phase are generated at equidistant locations separated by ![]() $2{\rm \pi} /k_g$, i.e. one wave-group length. Consequently, a de facto waveform with the same wavelength as the wave group forms and appears phase locked to the wave group, i.e. so-called bound subharmonic in previous studies. Similarly, in (3.27), the superposition of all the upwave-propagating free subharmonics leads to a downwave-propagating bound subharmonic. However, for an observer at a fixed observation position, the bound subharmonic does not exist because there is no space for the aforementioned superposition of the emitted free subharmonics to occur, which mathematically corresponds to an integral interval of zero length in (3.4), and only the free subharmonics arriving from elsewhere will be observed.
$2{\rm \pi} /k_g$, i.e. one wave-group length. Consequently, a de facto waveform with the same wavelength as the wave group forms and appears phase locked to the wave group, i.e. so-called bound subharmonic in previous studies. Similarly, in (3.27), the superposition of all the upwave-propagating free subharmonics leads to a downwave-propagating bound subharmonic. However, for an observer at a fixed observation position, the bound subharmonic does not exist because there is no space for the aforementioned superposition of the emitted free subharmonics to occur, which mathematically corresponds to an integral interval of zero length in (3.4), and only the free subharmonics arriving from elsewhere will be observed.
Interestingly, (3.26) shows that ![]() $\hat \xi _b^+ ( x )$ and
$\hat \xi _b^+ ( x )$ and ![]() $\hat \xi _b^- ( x )$ are respectively in antiphase and phase with the wave groups, and
$\hat \xi _b^- ( x )$ are respectively in antiphase and phase with the wave groups, and ![]() $| {\hat \xi _b^+ } |$ is
$| {\hat \xi _b^+ } |$ is ![]() $( k_g + k_f ) / ( k_g - k_f )$ times larger than
$( k_g + k_f ) / ( k_g - k_f )$ times larger than ![]() $| {\hat \xi _b^- } |$. Thus, the expression for the total bound subharmonics
$| {\hat \xi _b^- } |$. Thus, the expression for the total bound subharmonics ![]() ${\hat \xi _b} = \hat \xi _b^+ + \hat \xi _b^-$ is given by
${\hat \xi _b} = \hat \xi _b^+ + \hat \xi _b^-$ is given by
 \begin{equation} {\hat \xi _b}\left(x
\right) = \left[ {\frac{1}{{( {{k_g} + {k_f}} )}} - \frac{1}{{( {{k_g} - {k_f}} )}}}
\right]\frac{{k_g^2}}{{2{k_f}}}\frac{{\hat S\left( x
\right)}}{{\rho gh}} ={-} \frac{{k_g^2}}{{k_g^2 -
k_f^2}}\frac{{\hat S\left( x \right)}}{{\rho gh}},
\end{equation}
\begin{equation} {\hat \xi _b}\left(x
\right) = \left[ {\frac{1}{{( {{k_g} + {k_f}} )}} - \frac{1}{{( {{k_g} - {k_f}} )}}}
\right]\frac{{k_g^2}}{{2{k_f}}}\frac{{\hat S\left( x
\right)}}{{\rho gh}} ={-} \frac{{k_g^2}}{{k_g^2 -
k_f^2}}\frac{{\hat S\left( x \right)}}{{\rho gh}},
\end{equation}
which is in antiphase with the group forcing. Equation (3.28) is the same as the Reference Longuet-Higgins and StewartLHS62 solution:
 \begin{equation} {\hat \xi_{{{LHS62}}}}\left( x \right) ={-} \frac{{\hat S\left( x \right)}}{{\rho ( {gh - c_g^2})}}. \end{equation}
\begin{equation} {\hat \xi_{{{LHS62}}}}\left( x \right) ={-} \frac{{\hat S\left( x \right)}}{{\rho ( {gh - c_g^2})}}. \end{equation}3.2.2. Shallow water
In shallow water, ![]() $c_g \to \sqrt {gh}$ and
$c_g \to \sqrt {gh}$ and ![]() $k_g \to k_f$, the diagram in figure 4 changes to that in figure 5 and the emitted downwave-propagating subharmonics are now in phase with each other. This is because according to (3.12a) the phase of the downwave-propagating subharmonic emitted from
$k_g \to k_f$, the diagram in figure 4 changes to that in figure 5 and the emitted downwave-propagating subharmonics are now in phase with each other. This is because according to (3.12a) the phase of the downwave-propagating subharmonic emitted from ![]() $y$ is
$y$ is ![]() $\arg [\hat {\sigma }(\kern0.7pt y )\hat {\xi }_h^+(x)/\hat {\xi }_h^+(\kern0.7pt y )] \propto (k_g-k_f)y+k_fx$, which becomes independent of its source position
$\arg [\hat {\sigma }(\kern0.7pt y )\hat {\xi }_h^+(x)/\hat {\xi }_h^+(\kern0.7pt y )] \propto (k_g-k_f)y+k_fx$, which becomes independent of its source position ![]() $y$ as
$y$ as ![]() $k_g \to k_f$, indicating that all downwave-propagating subharmonics interfere with each other constructively. In addition, because the initial amplitudes of all the downwave subharmonics are the same, the superposed amplitude of
$k_g \to k_f$, indicating that all downwave-propagating subharmonics interfere with each other constructively. In addition, because the initial amplitudes of all the downwave subharmonics are the same, the superposed amplitude of ![]() $| {\hat \xi _g^+ } |$ increases proportionally with the number of forcing pulses, which in turn increases linearly with travel distance
$| {\hat \xi _g^+ } |$ increases proportionally with the number of forcing pulses, which in turn increases linearly with travel distance ![]() $k_g x$.
$k_g x$.

Figure 5. Same as figure 4, but for shallow water where ![]() $c_g=\sqrt {gh}$ and
$c_g=\sqrt {gh}$ and ![]() $k_g = k_f$, where
$k_g = k_f$, where ![]() $k_g=\omega _g/c_g$ and
$k_g=\omega _g/c_g$ and ![]() $k_f= \omega _g / \sqrt {gh}$ are wavenumbers of wave group and free subharmonic propagating as shallow-water wave, respectively. The vertical and horizontal white arrows denote the wavenumber of the emitted subharmonic component on the source and observation position, respectively. Values of the group-forcing lines in (b,c) are the same for reference.
$k_f= \omega _g / \sqrt {gh}$ are wavenumbers of wave group and free subharmonic propagating as shallow-water wave, respectively. The vertical and horizontal white arrows denote the wavenumber of the emitted subharmonic component on the source and observation position, respectively. Values of the group-forcing lines in (b,c) are the same for reference.

Figure 6. Amplitude (a,b) and phase (c,d) of the complex amplitude ![]() $\hat \xi (x)$ of the subharmonic surface elevation
$\hat \xi (x)$ of the subharmonic surface elevation ![]() $\tilde {\xi }(x,t)$ forced by bichromatic wave groups normally incident over a plane sloping bottom. Wave conditions and topography of tests A-4 (a,c) and B-5 (b,d) of the flume experiment of Van Noorloos (Reference Van Noorloos2003). Laboratory measurements (circles), the off-resonant solution of Zou (Reference Zou2011) ((B5), black dash-dotted lines), the near-resonance solution of Liao et al. (Reference Liao, Li, Liu and Zou2021) ((B7), black dashed lines), Janssen et al. (Reference Janssen, Battjes and van Dongeren2003) ((B8), black dotted lines), the present solution
$\tilde {\xi }(x,t)$ forced by bichromatic wave groups normally incident over a plane sloping bottom. Wave conditions and topography of tests A-4 (a,c) and B-5 (b,d) of the flume experiment of Van Noorloos (Reference Van Noorloos2003). Laboratory measurements (circles), the off-resonant solution of Zou (Reference Zou2011) ((B5), black dash-dotted lines), the near-resonance solution of Liao et al. (Reference Liao, Li, Liu and Zou2021) ((B7), black dashed lines), Janssen et al. (Reference Janssen, Battjes and van Dongeren2003) ((B8), black dotted lines), the present solution ![]() $\hat \xi =\hat \xi _g^+ + \hat \xi _{sc} + \hat \xi _g^-$ where
$\hat \xi =\hat \xi _g^+ + \hat \xi _{sc} + \hat \xi _g^-$ where ![]() $\hat \xi _{sc}$ denotes the downwave free subharmonic generated due to scattering at the slope toe ((B11), black solid lines) and its downwave- and upwave-propagating group-induced subharmonic components,
$\hat \xi _{sc}$ denotes the downwave free subharmonic generated due to scattering at the slope toe ((B11), black solid lines) and its downwave- and upwave-propagating group-induced subharmonic components, ![]() $\hat \xi _g^+$ (blue lines) and
$\hat \xi _g^+$ (blue lines) and ![]() $\hat \xi _g^-$ (red lines) in (B12). Phase is the phase lag with respect to wave groups plus
$\hat \xi _g^-$ (red lines) in (B12). Phase is the phase lag with respect to wave groups plus ![]() ${\rm \pi}$. Note that in (b), the phase of the upwave component
${\rm \pi}$. Note that in (b), the phase of the upwave component ![]() $\hat {\xi }_g^-$ was manually shifted by
$\hat {\xi }_g^-$ was manually shifted by ![]() ${\rm \pi}$ for plotting purposes.
${\rm \pi}$ for plotting purposes.
This result can also be derived by taking the limit ![]() $k_g \to k_f$ for
$k_g \to k_f$ for ![]() $\hat \xi _g^+$ in (3.27). From (2.10)–(2.11) we have
$\hat \xi _g^+$ in (3.27). From (2.10)–(2.11) we have ![]() $\hat {S}( x )=\hat {S}( a ) {\rm e}^{\text {i}{{k_g(x-a)}}}$ over a flat bottom. Substituting this for
$\hat {S}( x )=\hat {S}( a ) {\rm e}^{\text {i}{{k_g(x-a)}}}$ over a flat bottom. Substituting this for ![]() $\hat {S}( x )$ in (3.26) and subsequently (3.26) into (3.27) for
$\hat {S}( x )$ in (3.26) and subsequently (3.26) into (3.27) for ![]() $\hat {\xi }_g^+$ and then taking the limit
$\hat {\xi }_g^+$ and then taking the limit ![]() $k_g \to k_f$, we have
$k_g \to k_f$, we have
Thus, ![]() $| {\hat \xi _g^+ } |$ is proportional to the travel distance
$| {\hat \xi _g^+ } |$ is proportional to the travel distance ![]() ${k_g}( {x - a} )$. Equation (3.30) also shows that the downwave group-induced subharmonic leads the group forcing by
${k_g}( {x - a} )$. Equation (3.30) also shows that the downwave group-induced subharmonic leads the group forcing by ![]() ${\rm \pi} /2$ because of the complex factor
${\rm \pi} /2$ because of the complex factor ![]() $\mathrm {i}^{-1}$, since each emitted downwave-propagating subharmonic is initially ahead of the group forcing by
$\mathrm {i}^{-1}$, since each emitted downwave-propagating subharmonic is initially ahead of the group forcing by ![]() ${\rm \pi} /2$ according to (3.22).
${\rm \pi} /2$ according to (3.22).
Remarkably, in (3.30), the bound subharmonic cannot be distinguished from the free mode as in (3.27); hence, it is only meaningful to describe the superposed downwave-propagating group-induced subharmonic as a whole. This phenomenon indicates that ![]() $\hat \xi _b^+$ is released when the system is in full resonance. To some extent, it is consistent with the viewpoint of Baldock (Reference Baldock2012) that the bound subharmonic is released in shallow water with and without wave breaking. Nevertheless, the resonance only occurs in the propagating direction of group forcing, not in the upwave-propagating direction. Thereby, the present result partially differs from that of Baldock (Reference Baldock2012) in that the bound subharmonic component
$\hat \xi _b^+$ is released when the system is in full resonance. To some extent, it is consistent with the viewpoint of Baldock (Reference Baldock2012) that the bound subharmonic is released in shallow water with and without wave breaking. Nevertheless, the resonance only occurs in the propagating direction of group forcing, not in the upwave-propagating direction. Thereby, the present result partially differs from that of Baldock (Reference Baldock2012) in that the bound subharmonic component ![]() $\hat \xi _b^-$ still exists in shallow water. This can be found by taking the limit
$\hat \xi _b^-$ still exists in shallow water. This can be found by taking the limit ![]() $k_g \to k_f$ for
$k_g \to k_f$ for ![]() $\hat \xi _b^-$ in (3.26):
$\hat \xi _b^-$ in (3.26):
When the resonance occurs, ![]() $| {\hat \xi _g^+ } |$ far exceeds
$| {\hat \xi _g^+ } |$ far exceeds ![]() $| {\hat \xi _b^- } |$ after a certain distance (figure 5b,c), hence dominating
$| {\hat \xi _b^- } |$ after a certain distance (figure 5b,c), hence dominating ![]() $\hat \xi _g$.
$\hat \xi _g$.
3.3. Uneven bottom
Over an uneven bottom, assuming a mild bottom slope, i.e. ![]() $\vert \beta \vert = \vert h_x /(k_gh)\vert < \vert h_x/(k_fh)\vert \ll 1$ and
$\vert \beta \vert = \vert h_x /(k_gh)\vert < \vert h_x/(k_fh)\vert \ll 1$ and ![]() $h_{xx} /(k_gh)=O(\beta ^2)$, substituting (2.10) into the forcing field (3.2) yields
$h_{xx} /(k_gh)=O(\beta ^2)$, substituting (2.10) into the forcing field (3.2) yields
 \begin{equation} \hat f(x) = \frac{{k_g^2 \left| \hat S \right|}}{{\rho gh}}\left( { - \frac{1}{{k_g^2\left| {\hat S} \right|}}\frac{{{\mathrm{d}^2}\left| {\hat S} \right|}}{{\mathrm{d}\,{x^2}}} - \frac{{\rm 2i}}{{{k_g}\left| {\hat S} \right|}}\frac{{\mathrm{d}\left| {\hat S} \right|}}{{\mathrm{d}\,x}} - \frac{\rm i}{{k_g^2}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}\,x}} + 1} \right) {\rm e}^{\mathrm{i}\int^{x}k_g \,\mathrm{d}\,x'}. \end{equation}
\begin{equation} \hat f(x) = \frac{{k_g^2 \left| \hat S \right|}}{{\rho gh}}\left( { - \frac{1}{{k_g^2\left| {\hat S} \right|}}\frac{{{\mathrm{d}^2}\left| {\hat S} \right|}}{{\mathrm{d}\,{x^2}}} - \frac{{\rm 2i}}{{{k_g}\left| {\hat S} \right|}}\frac{{\mathrm{d}\left| {\hat S} \right|}}{{\mathrm{d}\,x}} - \frac{\rm i}{{k_g^2}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}\,x}} + 1} \right) {\rm e}^{\mathrm{i}\int^{x}k_g \,\mathrm{d}\,x'}. \end{equation} Following Zou (Reference Zou2011), (3.32) can be decomposed into ![]() ${\hat f_{{M}}}$ at leading order, which is the forcing field for a flat bottom in (3.19),
${\hat f_{{M}}}$ at leading order, which is the forcing field for a flat bottom in (3.19), ![]() $\hat f_{{S}}$ induced by bottom slope and
$\hat f_{{S}}$ induced by bottom slope and ![]() ${\hat f_{r}}$ due to higher-order bottom gradient
${\hat f_{r}}$ due to higher-order bottom gradient ![]() $h_x^2$ and
$h_x^2$ and ![]() ${h_{xx}}$, i.e.
${h_{xx}}$, i.e.
where
 \begin{equation}
\left. \begin{aligned} {{\hat f}_{{M}}} & = \frac{{k_g^2
\left| \hat S \right|}}{{\rho gh}}
\exp\left({\mathrm{i}\int^{x}k_g \,\mathrm{d}\,x'}\right),\\
{{\hat f}_{{S}}} & = {{\hat f}_{{M}}}\left( { -
\frac{{\text{2i}}}{{{k_g}\left| {\hat S}
\right|}}\frac{{\mathrm{d}\left| {\hat S}
\right|}}{{\mathrm{d}\,x}} -
\frac{\text{i}}{{k_g^2}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}\,x}}} \right) = {{\hat f}_{{M}}}O\left( \beta \right),\\
{{\hat f}_{{r}}} & = {{\hat f}_{{M}}}\left( { -
\frac{1}{{k_g^2\left| {\hat S}
\right|}}\frac{{{\mathrm{d}^2}\left| {\hat S}
\right|}}{{\mathrm{d}\,{x^2}}}} \right) = {{\hat
f}_{{M}}}O\left( {{\beta ^2}} \right), \end{aligned}
\right\}
\end{equation}
\begin{equation}
\left. \begin{aligned} {{\hat f}_{{M}}} & = \frac{{k_g^2
\left| \hat S \right|}}{{\rho gh}}
\exp\left({\mathrm{i}\int^{x}k_g \,\mathrm{d}\,x'}\right),\\
{{\hat f}_{{S}}} & = {{\hat f}_{{M}}}\left( { -
\frac{{\text{2i}}}{{{k_g}\left| {\hat S}
\right|}}\frac{{\mathrm{d}\left| {\hat S}
\right|}}{{\mathrm{d}\,x}} -
\frac{\text{i}}{{k_g^2}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}\,x}}} \right) = {{\hat f}_{{M}}}O\left( \beta \right),\\
{{\hat f}_{{r}}} & = {{\hat f}_{{M}}}\left( { -
\frac{1}{{k_g^2\left| {\hat S}
\right|}}\frac{{{\mathrm{d}^2}\left| {\hat S}
\right|}}{{\mathrm{d}\,{x^2}}}} \right) = {{\hat
f}_{{M}}}O\left( {{\beta ^2}} \right), \end{aligned}
\right\}
\end{equation}which is the same as the forcing field in Zou (Reference Zou2011).
The homogeneous solution in this case can be obtained by the perturbation method utilising the small parameter of ![]() $h_x/(k_fh)$. At leading order of
$h_x/(k_fh)$. At leading order of ![]() $O( 1 )$, the homogeneous solution is given by (cf. Zou Reference Zou2011, equation (3.9c))
$O( 1 )$, the homogeneous solution is given by (cf. Zou Reference Zou2011, equation (3.9c))
which is substituted into (3.10) to yield
Linearised to the first order of bottom slope, the forcing field (3.33) becomes
 \begin{equation} \hat{f}_{{L}} = \hat{f}_{{M}} + \hat{f}_{{S}} = \frac{{k_g^2 \left| \hat S \right|}}{{\rho gh}}\left( { 1 - \frac{{2{\rm i}}}{{{k_g}\left| {\hat S} \right|}}\frac{{\mathrm{d}\left| {\hat S} \right|}}{{\mathrm{d}\,x}} - \frac{\rm i}{{k_g^2}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}\,x}}} \right) \exp\left({\mathrm{i}\int^{x}k_g \,\mathrm{d}\,x'}\right), \end{equation}
\begin{equation} \hat{f}_{{L}} = \hat{f}_{{M}} + \hat{f}_{{S}} = \frac{{k_g^2 \left| \hat S \right|}}{{\rho gh}}\left( { 1 - \frac{{2{\rm i}}}{{{k_g}\left| {\hat S} \right|}}\frac{{\mathrm{d}\left| {\hat S} \right|}}{{\mathrm{d}\,x}} - \frac{\rm i}{{k_g^2}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}\,x}}} \right) \exp\left({\mathrm{i}\int^{x}k_g \,\mathrm{d}\,x'}\right), \end{equation}
which together with (3.36) are substituted into (3.7) to yield the expression for the source field ![]() $\hat \sigma (\kern0.7pt y )$:
$\hat \sigma (\kern0.7pt y )$:
 \begin{align} \hat \sigma(\kern0.7pt y ) = \frac{{k_g^2 \left| \hat S \right|}}{{2 \mathrm{i} k_f \rho gh}}\left( { 1 - \frac{{2{\rm i}}}{{{k_g}\left| {\hat S} \right|}}\frac{{\mathrm{d}\left| {\hat S} \right|}}{{\mathrm{d}\,x}} - \frac{\rm i}{{k_g^2}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}\,x}}} \right) \exp\left({\mathrm{i}\int^{y}k_g \,\mathrm{d}\,x'}\right) \left[ {1 + O\left( \beta{\frac{{{k_g}}}{{{k_f}}}} \right)} \right]. \end{align}
\begin{align} \hat \sigma(\kern0.7pt y ) = \frac{{k_g^2 \left| \hat S \right|}}{{2 \mathrm{i} k_f \rho gh}}\left( { 1 - \frac{{2{\rm i}}}{{{k_g}\left| {\hat S} \right|}}\frac{{\mathrm{d}\left| {\hat S} \right|}}{{\mathrm{d}\,x}} - \frac{\rm i}{{k_g^2}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}\,x}}} \right) \exp\left({\mathrm{i}\int^{y}k_g \,\mathrm{d}\,x'}\right) \left[ {1 + O\left( \beta{\frac{{{k_g}}}{{{k_f}}}} \right)} \right]. \end{align}Substituting (3.38) and (3.35) into (3.12a,b) yields
 \begin{equation}
\left. \begin{aligned} \hat \xi _g^+ \left( x \right) & =
\int_a^x {\frac{{{{\hat f}_{{L}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_f}\left(\kern0.7pt y \right)}}{{\left[
{\frac{{h\left( x \right)}}{{h\left(\kern0.7pt y \right)}}}
\right]}^{ - 0.25}} {\exp\left({\mathrm{i}\int_y^x
{{k_f}\,\mathrm{d}\,x'} }\right)} \left[ {1 + O\left(
\beta{\frac{{{k_g}}}{{{k_f}}}} \right)} \right]\,\mathrm{d} y}, \\
\hat \xi _g^- \left( x \right) & = \int_x^b
{\frac{{{{\hat f}_{{L}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_f}\left(\kern0.7pt y \right)}}{{\left[
{\frac{{h\left( x \right)}}{{h\left(\kern0.7pt y \right)}}}
\right]}^{ - 0.25}} {\exp\left({ - \mathrm{i}\int_y^x
{{k_f}\,\mathrm{d}\,x'} }\right)} \left[ {1 + O\left(
\beta{\frac{{{k_g}}}{{{k_f}}}} \right)} \right]\,\mathrm{d}
y}. \end{aligned} \right\}
\end{equation}
\begin{equation}
\left. \begin{aligned} \hat \xi _g^+ \left( x \right) & =
\int_a^x {\frac{{{{\hat f}_{{L}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_f}\left(\kern0.7pt y \right)}}{{\left[
{\frac{{h\left( x \right)}}{{h\left(\kern0.7pt y \right)}}}
\right]}^{ - 0.25}} {\exp\left({\mathrm{i}\int_y^x
{{k_f}\,\mathrm{d}\,x'} }\right)} \left[ {1 + O\left(
\beta{\frac{{{k_g}}}{{{k_f}}}} \right)} \right]\,\mathrm{d} y}, \\
\hat \xi _g^- \left( x \right) & = \int_x^b
{\frac{{{{\hat f}_{{L}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_f}\left(\kern0.7pt y \right)}}{{\left[
{\frac{{h\left( x \right)}}{{h\left(\kern0.7pt y \right)}}}
\right]}^{ - 0.25}} {\exp\left({ - \mathrm{i}\int_y^x
{{k_f}\,\mathrm{d}\,x'} }\right)} \left[ {1 + O\left(
\beta{\frac{{{k_g}}}{{{k_f}}}} \right)} \right]\,\mathrm{d}
y}. \end{aligned} \right\}
\end{equation}
The phase dependence of the integrand in (3.39) on source location ![]() $y$ determines the interference among all free components generated from different sources arriving at observation point
$y$ determines the interference among all free components generated from different sources arriving at observation point ![]() $x$. At leading order,
$x$. At leading order, ![]() $\hat f_{{L}}(\kern0.7pt y )$ in (3.37) is in phase with the wave group and hence its phase varies with
$\hat f_{{L}}(\kern0.7pt y )$ in (3.37) is in phase with the wave group and hence its phase varies with ![]() $y$ as
$y$ as ![]() $\int ^y{k_g}\,\mathrm {d}\,x'$. Therefore, in (3.39) the phase of each component of
$\int ^y{k_g}\,\mathrm {d}\,x'$. Therefore, in (3.39) the phase of each component of ![]() $\hat \xi ^\pm _g$ mainly varies with
$\hat \xi ^\pm _g$ mainly varies with ![]() $y$ as
$y$ as ![]() $\int ^y{k_g\pm k_f}\,\mathrm {d}\,x'$, which largely determines the relative magnitude between
$\int ^y{k_g\pm k_f}\,\mathrm {d}\,x'$, which largely determines the relative magnitude between ![]() $\hat \xi _g^+$ and
$\hat \xi _g^+$ and ![]() $\hat \xi _g^-$ as discussed in detail in Appendix C.
$\hat \xi _g^-$ as discussed in detail in Appendix C.
3.3.1. Shallow water
In shallow water, according to (3.26)–(3.27), as ![]() ${k_g} \to {k_f}$ and the resonance is intensified,
${k_g} \to {k_f}$ and the resonance is intensified, ![]() $\hat \xi _g^+$ becomes the predominant part of the group-induced subharmonic, i.e.
$\hat \xi _g^+$ becomes the predominant part of the group-induced subharmonic, i.e. ![]() ${\hat \xi _g} \approx \hat \xi _g^+$.
${\hat \xi _g} \approx \hat \xi _g^+$.
Without wave breaking, given the shallow-water approximations of ![]() $c_g\approx c \approx \sqrt {gh}$ and
$c_g\approx c \approx \sqrt {gh}$ and ![]() $k_g=\omega _g/c_g\approx \omega _g/\sqrt {gh}$, (2.11) indicates
$k_g=\omega _g/c_g\approx \omega _g/\sqrt {gh}$, (2.11) indicates ![]() $| {\hat S(x)} | = | {\hat S(a)} |\sqrt {h(a)/h(x)}$. Hence the spatial evolution of
$| {\hat S(x)} | = | {\hat S(a)} |\sqrt {h(a)/h(x)}$. Hence the spatial evolution of ![]() $\hat S$ described by the energy conservation (2.10)–(2.11) becomes
$\hat S$ described by the energy conservation (2.10)–(2.11) becomes
Substituting (3.40) into the forcing term (3.32) yields
at leading order.
Substituting (3.41) into the solution for ![]() $\hat \xi _g^+$ in (3.39) yields
$\hat \xi _g^+$ in (3.39) yields
at leading order, which is dependent on the bottom profile. The amplitude of ![]() $\hat \xi _g^+$ in (3.42) is proportional to
$\hat \xi _g^+$ in (3.42) is proportional to ![]() $\int _a^x {h{{(\kern0.7pt y )}^{ - 1.75}}\,\mathrm {d} y}$, which in turn is proportional to the horizontal length of the bottom profile between
$\int _a^x {h{{(\kern0.7pt y )}^{ - 1.75}}\,\mathrm {d} y}$, which in turn is proportional to the horizontal length of the bottom profile between ![]() $a$ and
$a$ and ![]() $x$. More specifically, suppose that the topography is horizontally stretched by a factor; considering the integrand in
$x$. More specifically, suppose that the topography is horizontally stretched by a factor; considering the integrand in ![]() $\int _a^x {h{{(\kern0.7pt y )}^{ - 1.75}}\,\mathrm {d} y}$ is only a function of depth, the integral covering the same bottom profile would also be enlarged by the same factor, and so is the amplitude of
$\int _a^x {h{{(\kern0.7pt y )}^{ - 1.75}}\,\mathrm {d} y}$ is only a function of depth, the integral covering the same bottom profile would also be enlarged by the same factor, and so is the amplitude of ![]() $\hat \xi _g^+$. This is essentially ascribed to the same accumulative constructive interference process of the downwave-propagating subharmonics demonstrated in figure 5, which causes the subharmonic amplitude to increase linearly with travel distance. This finding is consistent with the semi-analytical result of Liao et al. (Reference Liao, Li, Liu and Zou2021) that the amplitude of a group-induced subharmonic over the front slope of a shoal increases with the travel distance.
$\hat \xi _g^+$. This is essentially ascribed to the same accumulative constructive interference process of the downwave-propagating subharmonics demonstrated in figure 5, which causes the subharmonic amplitude to increase linearly with travel distance. This finding is consistent with the semi-analytical result of Liao et al. (Reference Liao, Li, Liu and Zou2021) that the amplitude of a group-induced subharmonic over the front slope of a shoal increases with the travel distance.
Over a uniform slope (![]() ${h_x} = {\textrm {const.}}$), (3.42) reduces to
${h_x} = {\textrm {const.}}$), (3.42) reduces to
 \begin{equation} \hat \xi _g^+ \left( x \right) = \frac{2\mathrm{i}}{3}\frac{{{\omega _g}}}{{{h_x}}}\sqrt {\frac{{h\left( a \right)}}{g}} \left[\frac{h(a)}{h(x)} - \left(\frac{h(a)}{h(x)}\right)^{0.25}\right]\frac{{\hat S\left( a \right)}}{{\rho gh\left( a \right)}} {\exp\left({\mathrm{i}\int_a^x {\frac{{{\omega _g}}}{{\sqrt {gh} }}\,\mathrm{d}\kern0.7pt x'} }\right)}. \end{equation}
\begin{equation} \hat \xi _g^+ \left( x \right) = \frac{2\mathrm{i}}{3}\frac{{{\omega _g}}}{{{h_x}}}\sqrt {\frac{{h\left( a \right)}}{g}} \left[\frac{h(a)}{h(x)} - \left(\frac{h(a)}{h(x)}\right)^{0.25}\right]\frac{{\hat S\left( a \right)}}{{\rho gh\left( a \right)}} {\exp\left({\mathrm{i}\int_a^x {\frac{{{\omega _g}}}{{\sqrt {gh} }}\,\mathrm{d}\kern0.7pt x'} }\right)}. \end{equation}Invoking (3.40) reduces (3.43) further to
 \begin{align} \hat \xi _g^+ \left( x \right) = \frac{2\mathrm{i}}{3}\frac{{{\omega _g}}}{{{h_x}}}\sqrt {\frac{{h\left( x \right)}}{g}} \frac{{\hat S\left( x \right)}}{{\rho gh\left( x \right)}} - \frac{{2\mathrm{i}}}{3}\frac{{{\omega _g}}}{{{h_x}}}\sqrt {\frac{{h\left( a \right)}}{g}} \frac{{\hat S\left( a \right)}}{{\rho gh\left( a \right)}}{\left[ {\frac{{h\left( x \right)}}{{h\left( a \right)}}} \right]^{ - 0.25}} {\exp\left({\mathrm{i}\int_a^x {\frac{{{\omega _g}}}{{\sqrt {gh} }}\,\mathrm{d}\,x'} }\right)}, \end{align}
\begin{align} \hat \xi _g^+ \left( x \right) = \frac{2\mathrm{i}}{3}\frac{{{\omega _g}}}{{{h_x}}}\sqrt {\frac{{h\left( x \right)}}{g}} \frac{{\hat S\left( x \right)}}{{\rho gh\left( x \right)}} - \frac{{2\mathrm{i}}}{3}\frac{{{\omega _g}}}{{{h_x}}}\sqrt {\frac{{h\left( a \right)}}{g}} \frac{{\hat S\left( a \right)}}{{\rho gh\left( a \right)}}{\left[ {\frac{{h\left( x \right)}}{{h\left( a \right)}}} \right]^{ - 0.25}} {\exp\left({\mathrm{i}\int_a^x {\frac{{{\omega _g}}}{{\sqrt {gh} }}\,\mathrm{d}\,x'} }\right)}, \end{align}
where the first term is consistent with the shallow-water limit of the near-resonant solution by equation (20) of Liao et al. (Reference Liao, Li, Liu and Zou2021) and the second term represents a free subharmonic. The second term appears because only the forcing inside the finite region ![]() $a$ to
$a$ to ![]() $x$ is considered; therefore,
$x$ is considered; therefore, ![]() $\hat \xi _g^+(a)=0$ has to be satisfied at the boundary
$\hat \xi _g^+(a)=0$ has to be satisfied at the boundary ![]() $x=a$. Equation (3.44) indicates that the amplitude of group-induced subharmonic is inversely proportional to the bottom slope in shallow water, which is due to the increase of group-induced subharmonic amplitude linearly with travel distance. This result provides a theoretical explanation for the well-known decrease of shoaling rate of group-induced subharmonic with the relative bottom slope (e.g. Battjes et al. Reference Battjes, Bakkenes, Janssen and van Dongeren2004; Van Dongeren et al. Reference Van Dongeren, Battjes, Janssen, Van Noorloos, Steenhauer, Steenbergen and Reniers2007; De Bakker, Tissier & Ruessink Reference De Bakker, Tissier and Ruessink2016; Zhang, Toorman & Monbaliu Reference Zhang, Toorman and Monbaliu2020). The dependence of subharmonic amplitude on the travel distance of wave groups corroborates the historical effect of spatial evolution of wave groups in the region of shallow water on the subharmonic amplitude in the subsequent region as previously studied by Li et al. (Reference Li, Liao, Liu and Zou2020) and Liao et al. (Reference Liao, Li, Liu and Zou2021). Apart from that, the present model indicates that the group-forcing field also affects the subharmonic on the upwave side because of the generation of those upwave-propagating subharmonics. The topographic effect on the group-induced subharmonics is examined in detail in Appendix D.
$x=a$. Equation (3.44) indicates that the amplitude of group-induced subharmonic is inversely proportional to the bottom slope in shallow water, which is due to the increase of group-induced subharmonic amplitude linearly with travel distance. This result provides a theoretical explanation for the well-known decrease of shoaling rate of group-induced subharmonic with the relative bottom slope (e.g. Battjes et al. Reference Battjes, Bakkenes, Janssen and van Dongeren2004; Van Dongeren et al. Reference Van Dongeren, Battjes, Janssen, Van Noorloos, Steenhauer, Steenbergen and Reniers2007; De Bakker, Tissier & Ruessink Reference De Bakker, Tissier and Ruessink2016; Zhang, Toorman & Monbaliu Reference Zhang, Toorman and Monbaliu2020). The dependence of subharmonic amplitude on the travel distance of wave groups corroborates the historical effect of spatial evolution of wave groups in the region of shallow water on the subharmonic amplitude in the subsequent region as previously studied by Li et al. (Reference Li, Liao, Liu and Zou2020) and Liao et al. (Reference Liao, Li, Liu and Zou2021). Apart from that, the present model indicates that the group-forcing field also affects the subharmonic on the upwave side because of the generation of those upwave-propagating subharmonics. The topographic effect on the group-induced subharmonics is examined in detail in Appendix D.
4. Comparisons of present and previous solutions
The present unified solution is shown to reduce to the existing solutions (Van Leeuwen Reference Van Leeuwen1992; Schäffer Reference Schäffer1993; Janssen et al. Reference Janssen, Battjes and van Dongeren2003; Zou Reference Zou2011; Contardo et al. Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and Symonds2021; Liao et al. Reference Liao, Li, Liu and Zou2021) in this section.
4.1. Solution over a plane sloping beach
The solution of the group-induced subharmonic over a plane sloping beach was obtained by Van Leeuwen (Reference Van Leeuwen1992) and Schäffer (Reference Schäffer1993). For a plane sloping beach with ![]() $x=0$ at the shoreline,
$x=0$ at the shoreline, ![]() $h = h_x x$, where
$h = h_x x$, where ![]() $h_x < 0$ is a constant, the governing equation (2.16) can be rewritten with the new dependent variable
$h_x < 0$ is a constant, the governing equation (2.16) can be rewritten with the new dependent variable
as
whose homogeneous solutions are given by
 \begin{equation} \left. \begin{aligned} \hat \xi_h^+(x) & = {\rm H}_0^{(2)}\left[ u(x) \right] = {\rm J}_0\left[ u(x) \right] - \mathrm{i}{\rm Y}_0\left[ u(x) \right],\\ \hat \xi_h^-(x) & = {\rm H}_0^{(1)}\left[ u(x) \right] = {\rm J}_0\left[ u(x) \right] + \mathrm{i}{\rm Y}_0\left[ u(x) \right], \end{aligned} \right\} \end{equation}
\begin{equation} \left. \begin{aligned} \hat \xi_h^+(x) & = {\rm H}_0^{(2)}\left[ u(x) \right] = {\rm J}_0\left[ u(x) \right] - \mathrm{i}{\rm Y}_0\left[ u(x) \right],\\ \hat \xi_h^-(x) & = {\rm H}_0^{(1)}\left[ u(x) \right] = {\rm J}_0\left[ u(x) \right] + \mathrm{i}{\rm Y}_0\left[ u(x) \right], \end{aligned} \right\} \end{equation}
where ![]() $\textrm {H}_0^{(1)}$ and
$\textrm {H}_0^{(1)}$ and ![]() $\textrm {H}_0^{(2)}$ are the first- and second-kind Hankel function of order zero and
$\textrm {H}_0^{(2)}$ are the first- and second-kind Hankel function of order zero and ![]() $\textrm {J}_0$ and
$\textrm {J}_0$ and ![]() $\textrm {Y}_0$ are the zeroth-order Bessel function of the first and second kind. Note that
$\textrm {Y}_0$ are the zeroth-order Bessel function of the first and second kind. Note that ![]() $\textrm {H}_0^{(2)}$ instead of
$\textrm {H}_0^{(2)}$ instead of ![]() $\textrm {H}_0^{(1)}$ becomes
$\textrm {H}_0^{(1)}$ becomes ![]() $\hat \xi _h^+(x)$ because as
$\hat \xi _h^+(x)$ because as ![]() $x$ increases the phase of
$x$ increases the phase of ![]() $\hat \xi _h^+(x)$ must increase. The Wronskian of
$\hat \xi _h^+(x)$ must increase. The Wronskian of ![]() $\hat \xi _h^-$ and
$\hat \xi _h^-$ and ![]() $\hat \xi _h^+$ in the denominator of (3.10) now becomes
$\hat \xi _h^+$ in the denominator of (3.10) now becomes
 \begin{align} & {\hat
\xi _h^-(x) \frac{\rm d}{{{\rm d}\,x}}\hat \xi _h^+(x) -
\hat \xi _h^+(x) \frac{\rm d}{{{\rm d}\,x}}\hat \xi _h^-(x) }\nonumber\\
&\quad = \left[{\rm
H}_0^{(1)}(u)\frac{\mathrm{d}}{\mathrm{d}u}{\rm
H}_0^{(2)}(u) - {\rm
H}_0^{(2)}(u)\frac{\mathrm{d}}{\mathrm{d}u}{\rm
H}_0^{(1)}(u)\right] \frac{\mathrm{d}u}{\mathrm{d}\,x}\nonumber\\
&\quad ={-}\frac{4 \mathrm{i}}{{\rm \pi}
u}\frac{\omega_g}{\sqrt{gh}} ={-}
\frac{2\mathrm{i}}{\rm \pi}\frac{h_x}{h}.
\end{align}
\begin{align} & {\hat
\xi _h^-(x) \frac{\rm d}{{{\rm d}\,x}}\hat \xi _h^+(x) -
\hat \xi _h^+(x) \frac{\rm d}{{{\rm d}\,x}}\hat \xi _h^-(x) }\nonumber\\
&\quad = \left[{\rm
H}_0^{(1)}(u)\frac{\mathrm{d}}{\mathrm{d}u}{\rm
H}_0^{(2)}(u) - {\rm
H}_0^{(2)}(u)\frac{\mathrm{d}}{\mathrm{d}u}{\rm
H}_0^{(1)}(u)\right] \frac{\mathrm{d}u}{\mathrm{d}\,x}\nonumber\\
&\quad ={-}\frac{4 \mathrm{i}}{{\rm \pi}
u}\frac{\omega_g}{\sqrt{gh}} ={-}
\frac{2\mathrm{i}}{\rm \pi}\frac{h_x}{h}.
\end{align}Substituting (3.2), (4.3) and (4.4) into (3.7) yields
Substituting (4.3) and (4.5) into the solution (3.16) yields
 $$\begin{align} \hat
\xi(x) &= {\rm H}_0^{(1)}\left[u(x)\right] \left[\frac{\hat
\xi_f^-(a)}{{\rm H}_0^{(1)}\left[u(a)\right]} +
\frac{\mathrm{i} {\rm \pi}}{2\rho g h_x} \int_{a}^{x} {\rm
H}_0^{(2)}[u(\kern0.7pt y )] \frac{\mathrm{d}^2 \hat
S}{\mathrm{d}\,x^2}\,\mathrm{d} y \right]\nonumber\\
&\quad + {\rm H}_0^{(2)}\left[u(x)\right] \left[\frac{\hat
\xi_f^+(a)}{{\rm H}_0^{(2)}\left[u(a)\right]} -
\frac{\mathrm{i} {\rm \pi}}{2\rho g h_x} \int_{a}^{x} {\rm
H}_0^{(1)}[u(\kern0.7pt y )] \frac{\mathrm{d}^2 \hat
S}{\mathrm{d}\,x^2}\,\mathrm{d} y \right],
\end{align}$$
$$\begin{align} \hat
\xi(x) &= {\rm H}_0^{(1)}\left[u(x)\right] \left[\frac{\hat
\xi_f^-(a)}{{\rm H}_0^{(1)}\left[u(a)\right]} +
\frac{\mathrm{i} {\rm \pi}}{2\rho g h_x} \int_{a}^{x} {\rm
H}_0^{(2)}[u(\kern0.7pt y )] \frac{\mathrm{d}^2 \hat
S}{\mathrm{d}\,x^2}\,\mathrm{d} y \right]\nonumber\\
&\quad + {\rm H}_0^{(2)}\left[u(x)\right] \left[\frac{\hat
\xi_f^+(a)}{{\rm H}_0^{(2)}\left[u(a)\right]} -
\frac{\mathrm{i} {\rm \pi}}{2\rho g h_x} \int_{a}^{x} {\rm
H}_0^{(1)}[u(\kern0.7pt y )] \frac{\mathrm{d}^2 \hat
S}{\mathrm{d}\,x^2}\,\mathrm{d} y \right],
\end{align}$$which is equivalent to the solution given by equation (4.16) in Schäffer (Reference Schäffer1993). Moreover, the non-homogeneous part of (4.6) can be easily converted to the solution given by equation (3.1.62) in Van Leeuwen (Reference Van Leeuwen1992) using the definition of Hankel function in (4.3).
4.2. Off-resonant solution for intermediate water
Let ![]() $\mu = 1 - k_f^2/k_g^2$ measure the departure of the system from resonance (Janssen et al. Reference Janssen, Battjes and van Dongeren2003), which decreases from
$\mu = 1 - k_f^2/k_g^2$ measure the departure of the system from resonance (Janssen et al. Reference Janssen, Battjes and van Dongeren2003), which decreases from ![]() $O(1)$ in intermediate water to zero in shallow water, and let
$O(1)$ in intermediate water to zero in shallow water, and let ![]() $\beta /\mu$ measure the resonance intensity of the system. The parameter regime of
$\beta /\mu$ measure the resonance intensity of the system. The parameter regime of ![]() $\beta {\mu ^{ - 1}} = O( \beta )$ in intermediate water and
$\beta {\mu ^{ - 1}} = O( \beta )$ in intermediate water and ![]() $\beta {\mu ^{ - 1}} = O( 1 )$ are referred to as off- and near-resonance conditions, respectively, as per Janssen et al. (Reference Janssen, Battjes and van Dongeren2003). Under off-resonant condition, Janssen et al. (Reference Janssen, Battjes and van Dongeren2003), Zou (Reference Zou2011) and Liao et al. (Reference Liao, Li, Liu and Zou2021) derived the analytical solution of subharmonic for uneven bottom using perturbation expansion with small parameter
$\beta {\mu ^{ - 1}} = O( 1 )$ are referred to as off- and near-resonance conditions, respectively, as per Janssen et al. (Reference Janssen, Battjes and van Dongeren2003). Under off-resonant condition, Janssen et al. (Reference Janssen, Battjes and van Dongeren2003), Zou (Reference Zou2011) and Liao et al. (Reference Liao, Li, Liu and Zou2021) derived the analytical solution of subharmonic for uneven bottom using perturbation expansion with small parameter ![]() $\beta$. Accurate to order
$\beta$. Accurate to order ![]() $O(\beta )$, their group-bounded subharmonic solutions are equivalent to each other:
$O(\beta )$, their group-bounded subharmonic solutions are equivalent to each other:
 \begin{align} {\hat
\xi _b} ={-} \frac{{\hat S}}{{\rho gh\mu }}\left\{ {1 +
\frac{{\mathrm{i}\beta }}{\mu }\left[ {\left(
{\frac{{2h}}{{\left| {\hat S} \right|}}\frac{{{\rm d}\left|
{\hat S} \right|}}{\mathrm{d}h} +
\frac{h}{{{k_g}}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}h}}}
\right)\left( {1 - \mu } \right) - 1 - \frac{{2h}}{\mu
}\frac{{\mathrm{d}\mu }}{{\mathrm{d}h}}} \right] + O({{\beta ^2}})} \right\}.
\end{align}
\begin{align} {\hat
\xi _b} ={-} \frac{{\hat S}}{{\rho gh\mu }}\left\{ {1 +
\frac{{\mathrm{i}\beta }}{\mu }\left[ {\left(
{\frac{{2h}}{{\left| {\hat S} \right|}}\frac{{{\rm d}\left|
{\hat S} \right|}}{\mathrm{d}h} +
\frac{h}{{{k_g}}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}h}}}
\right)\left( {1 - \mu } \right) - 1 - \frac{{2h}}{\mu
}\frac{{\mathrm{d}\mu }}{{\mathrm{d}h}}} \right] + O({{\beta ^2}})} \right\}.
\end{align} For an uneven bottom in intermediate water, the solution (3.11) can be first transformed into (3.39). The phase factor of the integrand in (3.39) is ![]() ${\exp ({\textrm {i}\int ^y {{k_g} \pm {k_f}\,\mathrm {d}\,x'} })}$ for
${\exp ({\textrm {i}\int ^y {{k_g} \pm {k_f}\,\mathrm {d}\,x'} })}$ for ![]() $\hat \xi _g^ \pm ( x )$, and applying the integration by parts technique to (3.39) using this phase factor twice, and retaining the variable upper bound of the integral, yields
$\hat \xi _g^ \pm ( x )$, and applying the integration by parts technique to (3.39) using this phase factor twice, and retaining the variable upper bound of the integral, yields
 $$\begin{align} \hat
\xi _b^ \pm &= \pm \frac{{{{\hat
f}_{{L}}}}}{{2\mathrm{i}{k_f}}}\left\{
{\frac{1}{{\mathrm{i}\left( {{k_g} \mp {k_f}} \right)}} +
\frac{1}{{{{\left( {{k_g} \mp {k_f}} \right)}^2}}}{{\left[
{\frac{{{h^{0.25}}{f_{{L}}}}}{{{k_f}\left( {{k_g} \mp
{k_f}} \right)}}} \right]}^{ -
1}}\frac{\mathrm{d}}{{\mathrm{d}\,x}}\left[
{\frac{{{h^{0.25}}{f_{{L}}}}}{{{k_f}\left( {{k_g} \mp
{k_f}} \right)}}} \right]} \right\}\nonumber\\
&\quad \times \left[ {1 + O\left( {\beta\frac{{{k_g}}}{{{k_f}}}} \right)}
\right],
\end{align}$$
$$\begin{align} \hat
\xi _b^ \pm &= \pm \frac{{{{\hat
f}_{{L}}}}}{{2\mathrm{i}{k_f}}}\left\{
{\frac{1}{{\mathrm{i}\left( {{k_g} \mp {k_f}} \right)}} +
\frac{1}{{{{\left( {{k_g} \mp {k_f}} \right)}^2}}}{{\left[
{\frac{{{h^{0.25}}{f_{{L}}}}}{{{k_f}\left( {{k_g} \mp
{k_f}} \right)}}} \right]}^{ -
1}}\frac{\mathrm{d}}{{\mathrm{d}\,x}}\left[
{\frac{{{h^{0.25}}{f_{{L}}}}}{{{k_f}\left( {{k_g} \mp
{k_f}} \right)}}} \right]} \right\}\nonumber\\
&\quad \times \left[ {1 + O\left( {\beta\frac{{{k_g}}}{{{k_f}}}} \right)}
\right],
\end{align}$$
where ![]() ${f_{{L}}} = {\hat f_{{L}}}| {\hat S} |{\hat S^{ - 1}} = (\kern0.7pt {{{\hat f}_{{M}}} + {{\hat f}_{{S}}}} )| {\hat S} |{\hat S^{ - 1}}$ is the linearised forcing term excluding the phase factor of wave group.
${f_{{L}}} = {\hat f_{{L}}}| {\hat S} |{\hat S^{ - 1}} = (\kern0.7pt {{{\hat f}_{{M}}} + {{\hat f}_{{S}}}} )| {\hat S} |{\hat S^{ - 1}}$ is the linearised forcing term excluding the phase factor of wave group.
Substituting (3.37) and ![]() $\mu = 1 - k_f^2/k_g^2$ into (4.8), we have
$\mu = 1 - k_f^2/k_g^2$ into (4.8), we have
 \begin{align}
\hat{\xi}_{b}^{{\pm}}(x)={\mp} \frac{\hat{S}}{\rho g h \mu}
\frac{k_{g} \pm k_{f}}{2 k_{f}}\left[\begin{array}{@{}l@{}}
\left(1-\dfrac{2 \mathrm{i}}{k_{g}|\hat{S}|}
\dfrac{\mathrm{d}|\hat{S}|}{\mathrm{d}\,x}-\dfrac{\mathrm{i}}{k_{g}^{2}} \dfrac{\mathrm{d}
k_{g}}{\mathrm{d}\,x}\right)-\dfrac{k_{g} \pm
k_{f}}{\mathrm{i} k_{g}^{2}
\mu}\left(\dfrac{|\hat{S}|}{h^{0.25} \mu}\right)^{{-}1} \\
\quad \times \dfrac{\mathrm{d}}{\mathrm{d}\,x}\left(\dfrac{|\hat{S}|}{h^{0.25} \mu}\right)
-\dfrac{1}{\mathrm{i} k_{g}^{2} \mu}
\dfrac{\mathrm{d}}{\mathrm{d}\,x}\left(k_{g} \pm
k_{f}\right)+O\left(\beta\dfrac{k_{g}}{k_{f}}\right)
\end{array}\right].
\end{align}
\begin{align}
\hat{\xi}_{b}^{{\pm}}(x)={\mp} \frac{\hat{S}}{\rho g h \mu}
\frac{k_{g} \pm k_{f}}{2 k_{f}}\left[\begin{array}{@{}l@{}}
\left(1-\dfrac{2 \mathrm{i}}{k_{g}|\hat{S}|}
\dfrac{\mathrm{d}|\hat{S}|}{\mathrm{d}\,x}-\dfrac{\mathrm{i}}{k_{g}^{2}} \dfrac{\mathrm{d}
k_{g}}{\mathrm{d}\,x}\right)-\dfrac{k_{g} \pm
k_{f}}{\mathrm{i} k_{g}^{2}
\mu}\left(\dfrac{|\hat{S}|}{h^{0.25} \mu}\right)^{{-}1} \\
\quad \times \dfrac{\mathrm{d}}{\mathrm{d}\,x}\left(\dfrac{|\hat{S}|}{h^{0.25} \mu}\right)
-\dfrac{1}{\mathrm{i} k_{g}^{2} \mu}
\dfrac{\mathrm{d}}{\mathrm{d}\,x}\left(k_{g} \pm
k_{f}\right)+O\left(\beta\dfrac{k_{g}}{k_{f}}\right)
\end{array}\right].
\end{align}
Adding ![]() $\hat \xi _b^+$ and
$\hat \xi _b^+$ and ![]() $\hat \xi _b^-$ in (4.9) yields
$\hat \xi _b^-$ in (4.9) yields
 \begin{align} {\hat \xi _b} &= \hat \xi _b^+ + \hat \xi _b^- \nonumber\\ &={-} \frac{{\hat S}}{{\rho gh\mu }}\left\{ {1 + \frac{{\mathrm{i}\beta }}{\mu }\left[ {\left( {\frac{{2h}}{{\left| {\hat S} \right|}}\frac{{\mathrm{d}\left| {\hat S} \right|}}{{\mathrm{d}h}} + \frac{h}{{{k_g}}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}h}}} \right)\left( {1 - \mu } \right) - 1 - \frac{{2h}}{\mu }\frac{{\mathrm{d}\mu }}{{\mathrm{d}h}}} \right] + O\left( {{\beta ^2}} \right)} \right\}, \end{align}
\begin{align} {\hat \xi _b} &= \hat \xi _b^+ + \hat \xi _b^- \nonumber\\ &={-} \frac{{\hat S}}{{\rho gh\mu }}\left\{ {1 + \frac{{\mathrm{i}\beta }}{\mu }\left[ {\left( {\frac{{2h}}{{\left| {\hat S} \right|}}\frac{{\mathrm{d}\left| {\hat S} \right|}}{{\mathrm{d}h}} + \frac{h}{{{k_g}}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}h}}} \right)\left( {1 - \mu } \right) - 1 - \frac{{2h}}{\mu }\frac{{\mathrm{d}\mu }}{{\mathrm{d}h}}} \right] + O\left( {{\beta ^2}} \right)} \right\}, \end{align}
which is the same as solution (4.7). Note that the relative error for ![]() $\hat \xi _b^ \pm$ in (4.9) is of
$\hat \xi _b^ \pm$ in (4.9) is of ![]() $O[ h_x/ (k_fh)]$, but the error for
$O[ h_x/ (k_fh)]$, but the error for ![]() ${\hat \xi _b}$ in (4.10) is of
${\hat \xi _b}$ in (4.10) is of ![]() $O( \beta ^2 )$ (see Appendix A for more details).
$O( \beta ^2 )$ (see Appendix A for more details).
4.3. Near-resonant solution for shallow water
4.3.1. Liao et al. (2021) solution
In the case of near resonance in shallow water ![]() $(\beta \mu ^{ - 1} = O(1) )$, Liao et al. (Reference Liao, Li, Liu and Zou2021) derived the following solution of group-induced subharmonic (cf. equation (19) therein):
$(\beta \mu ^{ - 1} = O(1) )$, Liao et al. (Reference Liao, Li, Liu and Zou2021) derived the following solution of group-induced subharmonic (cf. equation (19) therein):
 \begin{align} {\hat \xi _g}\left( x \right) ={-} \frac{{\mathrm{i}\hat S\left( x \right)}}{{2\rho gh\left( x \right)}}\int_a^x {\left| {\frac{{\hat S\left(\kern0.7pt y \right)}}{{\hat S\left( x \right)}}} \right|\sqrt {\frac{{{k_g}\left(\kern0.7pt y \right)h\left( x \right)}}{{{k_g}\left( x \right)h\left(\kern0.7pt y \right)}}} {k_g}\left(\kern0.7pt y \right) {\exp\left({ - \mathrm{i}\int_y^x {\frac{\mu }{2}{k_g}\,\mathrm{d}\,x'} }\right)}\,\mathrm{d} y} \left[ {1 + O\left( \beta \right)} \right]. \end{align}
\begin{align} {\hat \xi _g}\left( x \right) ={-} \frac{{\mathrm{i}\hat S\left( x \right)}}{{2\rho gh\left( x \right)}}\int_a^x {\left| {\frac{{\hat S\left(\kern0.7pt y \right)}}{{\hat S\left( x \right)}}} \right|\sqrt {\frac{{{k_g}\left(\kern0.7pt y \right)h\left( x \right)}}{{{k_g}\left( x \right)h\left(\kern0.7pt y \right)}}} {k_g}\left(\kern0.7pt y \right) {\exp\left({ - \mathrm{i}\int_y^x {\frac{\mu }{2}{k_g}\,\mathrm{d}\,x'} }\right)}\,\mathrm{d} y} \left[ {1 + O\left( \beta \right)} \right]. \end{align}
The relationship ![]() $\hat {S}(x) /|\hat {S}(x)|=\hat {S}(\kern0.7pt y ) /|\hat {S}(\kern0.7pt y )| \exp (\mathrm {i} \int _{y}^{x} k_{g}\, {\textrm {d}\kern0.7pt x}^{\prime })$ could be derived from (2.10) and then substituted together with
$\hat {S}(x) /|\hat {S}(x)|=\hat {S}(\kern0.7pt y ) /|\hat {S}(\kern0.7pt y )| \exp (\mathrm {i} \int _{y}^{x} k_{g}\, {\textrm {d}\kern0.7pt x}^{\prime })$ could be derived from (2.10) and then substituted together with ![]() ${\hat f_{{M}}}$ in (3.34) into (4.11) to obtain
${\hat f_{{M}}}$ in (3.34) into (4.11) to obtain
 \begin{equation} {\hat \xi _g}\left( x \right) = \int_a^x {\frac{{{{\hat f}_{{M}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_g}\left(\kern0.7pt y \right)}}\left[ {1 + O\left( \beta \right)} \right]\sqrt {\frac{{{k_g}\left(\kern0.7pt y \right)h\left(\kern0.7pt y \right)}}{{{k_g}\left( x \right)h\left( x \right)}}} {\exp\left({\mathrm{i}\int_y^x {\left( {1 - \frac{\mu }{2}} \right){k_g}\,\mathrm{d}\,x'} }\right)}\,\mathrm{d} y} . \end{equation}
\begin{equation} {\hat \xi _g}\left( x \right) = \int_a^x {\frac{{{{\hat f}_{{M}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_g}\left(\kern0.7pt y \right)}}\left[ {1 + O\left( \beta \right)} \right]\sqrt {\frac{{{k_g}\left(\kern0.7pt y \right)h\left(\kern0.7pt y \right)}}{{{k_g}\left( x \right)h\left( x \right)}}} {\exp\left({\mathrm{i}\int_y^x {\left( {1 - \frac{\mu }{2}} \right){k_g}\,\mathrm{d}\,x'} }\right)}\,\mathrm{d} y} . \end{equation}
In this condition, (3.26)–(3.27) indicate that ![]() $| {\hat \xi _g^+ } |$ is greater than
$| {\hat \xi _g^+ } |$ is greater than ![]() $| {\hat \xi _g^- } |$ by an order of factor
$| {\hat \xi _g^- } |$ by an order of factor ![]() $(k_{g}+k_{f}) /(k_{g}-k_{f})=(1+\sqrt {1-\mu }) /(1-\sqrt {1-\mu })$, which is of
$(k_{g}+k_{f}) /(k_{g}-k_{f})=(1+\sqrt {1-\mu }) /(1-\sqrt {1-\mu })$, which is of ![]() $O( \mu ^{ - 1} ) = O( \beta ^{ - 1} )$ for
$O( \mu ^{ - 1} ) = O( \beta ^{ - 1} )$ for ![]() $\mu = O( \beta ) \ll 1$ in shallow water. Besides, as shown in Appendix A, the error of (3.39) is now of
$\mu = O( \beta ) \ll 1$ in shallow water. Besides, as shown in Appendix A, the error of (3.39) is now of ![]() $O(\beta )$ relative to leading order, and hence we aim to prove that the solution for
$O(\beta )$ relative to leading order, and hence we aim to prove that the solution for ![]() $\hat \xi _g^+$ in (3.39) at leading order
$\hat \xi _g^+$ in (3.39) at leading order
 \begin{equation} {\hat \xi _g}\left( x \right) = \int_a^x {\frac{{{{\hat f}_{{M}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_f}\left(\kern0.7pt y \right)}}\left[ {1 + O\left( \beta \right)} \right]{{\left[ {\frac{{h\left( x \right)}}{{h\left(\kern0.7pt y \right)}}} \right]}^{ - 0.25}} {\exp\left({\mathrm{i}\int_y^x {{k_f}\,\mathrm{d}\,x'} }\right)}\,\mathrm{d} y} \end{equation}
\begin{equation} {\hat \xi _g}\left( x \right) = \int_a^x {\frac{{{{\hat f}_{{M}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_f}\left(\kern0.7pt y \right)}}\left[ {1 + O\left( \beta \right)} \right]{{\left[ {\frac{{h\left( x \right)}}{{h\left(\kern0.7pt y \right)}}} \right]}^{ - 0.25}} {\exp\left({\mathrm{i}\int_y^x {{k_f}\,\mathrm{d}\,x'} }\right)}\,\mathrm{d} y} \end{equation}is consistent with (4.12).
Because ![]() $k_{f} / k_{g}=\sqrt {1-\mu }=1+O(\beta )$ and
$k_{f} / k_{g}=\sqrt {1-\mu }=1+O(\beta )$ and ![]() $k_{g}-k_{f}=k_{g}(1-\sqrt {1-\mu })=k_{g}[\mu / 2+O(\beta ^{2})]$, hence
$k_{g}-k_{f}=k_{g}(1-\sqrt {1-\mu })=k_{g}[\mu / 2+O(\beta ^{2})]$, hence ![]() $[1-\mu /2+O(\beta ^2)]k_g=k_f$ and at leading order the integrands of (4.12) and (4.13) are consistent with each other and so are the two solutions.
$[1-\mu /2+O(\beta ^2)]k_g=k_f$ and at leading order the integrands of (4.12) and (4.13) are consistent with each other and so are the two solutions.
4.3.2. Janssen et al. (2003) solution
For the near-resonance condition ![]() $(\beta \mu ^{-1} = O(1) )$, Janssen et al. (Reference Janssen, Battjes and van Dongeren2003) derived the following governing equation for the complex amplitude of subharmonic
$(\beta \mu ^{-1} = O(1) )$, Janssen et al. (Reference Janssen, Battjes and van Dongeren2003) derived the following governing equation for the complex amplitude of subharmonic ![]() $\hat \xi$ (equation (23) therein). Using the notations of the present study, it reads as
$\hat \xi$ (equation (23) therein). Using the notations of the present study, it reads as
 \begin{align}
\frac{\mathrm{d} \hat{\xi}}{\mathrm{d}\,x} +
\hat{\xi}\left[\frac{h_x}{2h} + \frac{(k_g)_x}{2k_g} +
\mathrm{i} k_g (\frac{\mu}{2} - 1)\right] ={-}
\frac{\mathrm{i}k_g \hat{S}}{2 \rho gh}\left(1 -
\frac{2\mathrm{i}k_g \left|\hat{S}\right|_x}{k_g
\left|\hat{S}\right|} - \frac{\mathrm{i}
(k_g)_x}{k_g^2}\right) + O(\beta^2).
\end{align}
\begin{align}
\frac{\mathrm{d} \hat{\xi}}{\mathrm{d}\,x} +
\hat{\xi}\left[\frac{h_x}{2h} + \frac{(k_g)_x}{2k_g} +
\mathrm{i} k_g (\frac{\mu}{2} - 1)\right] ={-}
\frac{\mathrm{i}k_g \hat{S}}{2 \rho gh}\left(1 -
\frac{2\mathrm{i}k_g \left|\hat{S}\right|_x}{k_g
\left|\hat{S}\right|} - \frac{\mathrm{i}
(k_g)_x}{k_g^2}\right) + O(\beta^2).
\end{align} Recalling the expressions for the leading- and first-order forcing terms ( ![]() $\hat {f}_{M}$ and
$\hat {f}_{M}$ and ![]() $\hat {f}_S$; equation (3.34)), (4.14) reduces to
$\hat {f}_S$; equation (3.34)), (4.14) reduces to
 \begin{equation} \frac{\mathrm{d}
\hat{\xi}}{\mathrm{d}\,x} + \hat{\xi}\Biggl[\frac{h_x}{2h} +
\frac{(k_g)_x}{2k_g} + \mathrm{i} k_g \Biggl(\frac{\mu}{2} -
1\Biggr)\Biggr] = \frac{1}{2\mathrm{i}k_g}(\hat{f}_{M} +
\hat{f}_S) + O(\beta^2),
\end{equation}
\begin{equation} \frac{\mathrm{d}
\hat{\xi}}{\mathrm{d}\,x} + \hat{\xi}\Biggl[\frac{h_x}{2h} +
\frac{(k_g)_x}{2k_g} + \mathrm{i} k_g \Biggl(\frac{\mu}{2} -
1\Biggr)\Biggr] = \frac{1}{2\mathrm{i}k_g}(\hat{f}_{M} +
\hat{f}_S) + O(\beta^2),
\end{equation}
which has the solution
 \begin{equation} {\hat \xi _g}\left( x \right) = \int_a^x {\frac{{{{\hat f}_{{M}}(\kern0.7pt y ) + {\hat f}_{{S}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_g}\left(\kern0.7pt y \right)}}\sqrt {\frac{{{k_g}\left(\kern0.7pt y \right)h\left(\kern0.7pt y \right)}}{{{k_g}\left( x \right)h\left( x \right)}}} {\exp\Biggl({\mathrm{i}\int_y^x {\Biggl( {1 - \frac{\mu }{2}} \Biggr){k_g}\,\mathrm{d}\,x'} }\Biggr)}\,\mathrm{d} y} . \end{equation}
\begin{equation} {\hat \xi _g}\left( x \right) = \int_a^x {\frac{{{{\hat f}_{{M}}(\kern0.7pt y ) + {\hat f}_{{S}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_g}\left(\kern0.7pt y \right)}}\sqrt {\frac{{{k_g}\left(\kern0.7pt y \right)h\left(\kern0.7pt y \right)}}{{{k_g}\left( x \right)h\left( x \right)}}} {\exp\Biggl({\mathrm{i}\int_y^x {\Biggl( {1 - \frac{\mu }{2}} \Biggr){k_g}\,\mathrm{d}\,x'} }\Biggr)}\,\mathrm{d} y} . \end{equation}At leading order, (4.16) is equivalent to the solution of Liao et al. (Reference Liao, Li, Liu and Zou2021) (equation (4.12) therein), which has been demonstrated above to be equivalent to the present solution (4.13).
Figure 6 shows the theoretical predictions of the amplitude and phase of group-induced subharmonic on a plane sloping bottom under the conditions of the A-4 and B-5 series in the bichromatic wave experiment of Van Noorloos (Reference Van Noorloos2003) using the off-resonant solution of Zou (Reference Zou2011), the near-resonant solutions of Liao et al. (Reference Liao, Li, Liu and Zou2021) and Janssen et al. (Reference Janssen, Battjes and van Dongeren2003) and the present solution. To compare with laboratory measurements, the free subharmonic generated due to scattering at the toe of the slope was also calculated and added to the group-induced subharmonic in figure 6 (see Appendix B for details of calculation). Note that although the component ![]() $\hat \xi _g^-$ is induced by upwave-propagating free subharmonics, its waveform actually propagates in the downwave direction as indicated by
$\hat \xi _g^-$ is induced by upwave-propagating free subharmonics, its waveform actually propagates in the downwave direction as indicated by ![]() $\hat \xi _b^-$ in (3.27) and (4.9) as well as the slowly varying phase difference between
$\hat \xi _b^-$ in (3.27) and (4.9) as well as the slowly varying phase difference between ![]() $\hat \xi _g^-$ and the wave group (red lines in figure 6c,d). For this reason, and also because the incoming and outgoing subharmonics were separated in Van Noorloos (Reference Van Noorloos2003) by detecting the propagation of waveform, the component
$\hat \xi _g^-$ and the wave group (red lines in figure 6c,d). For this reason, and also because the incoming and outgoing subharmonics were separated in Van Noorloos (Reference Van Noorloos2003) by detecting the propagation of waveform, the component ![]() $\hat \xi _g^-$ should be included in the total solution
$\hat \xi _g^-$ should be included in the total solution ![]() $\hat \xi _g^+ + \hat \xi _{sc} + \hat \xi _g^-$ to compare with the incoming subharmonic in Van Noorloos (Reference Van Noorloos2003) (circles in figure 6).
$\hat \xi _g^+ + \hat \xi _{sc} + \hat \xi _g^-$ to compare with the incoming subharmonic in Van Noorloos (Reference Van Noorloos2003) (circles in figure 6).
As the water depth diminishes, the amplitude predicted by the off-resonant solution of Zou (Reference Zou2011) diverges as expected; the near-resonant solution of Janssen et al. (Reference Janssen, Battjes and van Dongeren2003) slightly overestimated the subharmonic amplitude but underestimated the subharmonic phase lag behind the wave group. The near-resonant solution of Liao et al. (Reference Liao, Li, Liu and Zou2021) predicts the amplitude similar to the present solution but with lower phase lag. Among the three near-resonant solutions included, the present solution agrees with laboratory measurements the best. In addition, figure 6 also indicates that in shallow water, the downwave-propagating group-induced subharmonic ![]() $\hat \xi _g^+$ eventually dominates the group-induced subharmonic, thus becoming the major contributor to both its amplitude and phase. Despite the dominance of
$\hat \xi _g^+$ eventually dominates the group-induced subharmonic, thus becoming the major contributor to both its amplitude and phase. Despite the dominance of ![]() $\hat \xi _g^+$, however, discernible discrepancy between the total solution
$\hat \xi _g^+$, however, discernible discrepancy between the total solution ![]() $\hat \xi _g^+ + \hat \xi _{sc} + \hat \xi _g^-$ (black solid lines) and the downwave-propagating component
$\hat \xi _g^+ + \hat \xi _{sc} + \hat \xi _g^-$ (black solid lines) and the downwave-propagating component ![]() $\hat \xi _g^+$ remains over the full depth range. The disagreement between experiment and theory becomes more evident at deeper water for scenario of test B-5 than A-4, due to the larger primary wave amplitude
$\hat \xi _g^+$ remains over the full depth range. The disagreement between experiment and theory becomes more evident at deeper water for scenario of test B-5 than A-4, due to the larger primary wave amplitude ![]() $A_1+A_2$ and therefore the onset of wave breaking at deeper water. This is discussed further in figure 10.
$A_1+A_2$ and therefore the onset of wave breaking at deeper water. This is discussed further in figure 10.
4.3.3. Contardo et al. (2021) solution
Contardo et al. (Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and Symonds2021) discretised a 1-D topography into a succession of small steps. By applying the Reference Longuet-Higgins and StewartLHS62 solution for the flat bottom on both sides of the step and applying the mass and momentum matching conditions across the step, the scattered free subharmonics induced by the wave group propagating across each single depth discontinuity were calculated. Assuming an in-phase relationship with the wave radiation stress, the initial complex amplitude of the transmitted free subharmonic is given by
 \begin{equation} {\hat \sigma
_{{{CLHRDS21}}}}\left( x \right) = \frac{{\left. {\left({\left| {{{\hat \xi }_{{{LHS62}}}}} \right|{k_g}h}\right)}
\right|_{{x-\Delta x}}^x + {{\left. {( {{k_f}h})} \right|}_{{x-\Delta x}}}\left. {\left( {\left|
{{{\hat \xi }_{{{LHS62}}}}} \right|} \right)}
\right|_{{x-\Delta x}}^x}}{{{{\left. {( {{k_f}h})} \right|}_{{x-\Delta x}}} + {{\left.
{( {{k_f}h} )} \right|}_{{x}}}}}\frac{{\hat S}}{{\left|
{\hat S} \right|}}, \end{equation}
\begin{equation} {\hat \sigma
_{{{CLHRDS21}}}}\left( x \right) = \frac{{\left. {\left({\left| {{{\hat \xi }_{{{LHS62}}}}} \right|{k_g}h}\right)}
\right|_{{x-\Delta x}}^x + {{\left. {( {{k_f}h})} \right|}_{{x-\Delta x}}}\left. {\left( {\left|
{{{\hat \xi }_{{{LHS62}}}}} \right|} \right)}
\right|_{{x-\Delta x}}^x}}{{{{\left. {( {{k_f}h})} \right|}_{{x-\Delta x}}} + {{\left.
{( {{k_f}h} )} \right|}_{{x}}}}}\frac{{\hat S}}{{\left|
{\hat S} \right|}}, \end{equation}
where ![]() ${{ {} |}_{x-\Delta x}}$ and
${{ {} |}_{x-\Delta x}}$ and ![]() ${{ {} |}_{x}}$ denote the quantities at the locations immediately before (
${{ {} |}_{x}}$ denote the quantities at the locations immediately before (![]() $x-\Delta x$) and after (
$x-\Delta x$) and after (![]() $x$) the step respectively, corresponding to the subscripts ‘sea’ and ‘shore’ adopted by Contardo et al. (Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and Symonds2021), and
$x$) the step respectively, corresponding to the subscripts ‘sea’ and ‘shore’ adopted by Contardo et al. (Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and Symonds2021), and ![]() ${} |_{x-\Delta x}^{x}$ denotes the difference between the variables at
${} |_{x-\Delta x}^{x}$ denotes the difference between the variables at ![]() $x$ and
$x$ and ![]() $x-\Delta x$. The total downwave subharmonic is the superposition of the bound subharmonic as described by Reference Longuet-Higgins and StewartLHS62 and all the transmitted free subharmonics generated over the steps through which the wave groups have passed. In the case of continuous depth change, consider that the depth changes from
$x-\Delta x$. The total downwave subharmonic is the superposition of the bound subharmonic as described by Reference Longuet-Higgins and StewartLHS62 and all the transmitted free subharmonics generated over the steps through which the wave groups have passed. In the case of continuous depth change, consider that the depth changes from ![]() $h( x-\Delta x )$ to
$h( x-\Delta x )$ to ![]() $h( x )$ within a small distance
$h( x )$ within a small distance ![]() $\Delta x$ and then taking the limit
$\Delta x$ and then taking the limit ![]() $\Delta x \to 0$ yields
$\Delta x \to 0$ yields
 \begin{equation} {\hat \sigma _{{{CLHRDS21}}}}\left( x \right) = \left[ {\frac{{{k_g} + {k_f}}}{{2{k_f}}}\frac{{\mathrm{d}\left| {{{\hat \xi }_{{{LHS62}}}}} \right|}}{{\mathrm{d}\,x}} + \frac{{\left| {{{\hat \xi }_{{{LHS62}}}}} \right|}}{{2{k_f}h}}\frac{{\mathrm{d}({{k_g}h})}}{{\mathrm{d}\,x}}} \right]\frac{{\hat S}}{{\left| {\hat S} \right|}}, \end{equation}
\begin{equation} {\hat \sigma _{{{CLHRDS21}}}}\left( x \right) = \left[ {\frac{{{k_g} + {k_f}}}{{2{k_f}}}\frac{{\mathrm{d}\left| {{{\hat \xi }_{{{LHS62}}}}} \right|}}{{\mathrm{d}\,x}} + \frac{{\left| {{{\hat \xi }_{{{LHS62}}}}} \right|}}{{2{k_f}h}}\frac{{\mathrm{d}({{k_g}h})}}{{\mathrm{d}\,x}}} \right]\frac{{\hat S}}{{\left| {\hat S} \right|}}, \end{equation}
which, as shown below, is consistent with the present solution after subtracting the Reference Longuet-Higgins and StewartLHS62 solution from ![]() $\hat \xi _g^+$ in (4.13) at leading order.
$\hat \xi _g^+$ in (4.13) at leading order.
With the phase factor ![]() ${\exp ({\mathrm {i}\int ^y {{k_g}\,\mathrm {d}\,x'} })}$ in
${\exp ({\mathrm {i}\int ^y {{k_g}\,\mathrm {d}\,x'} })}$ in ![]() ${\hat f_{{M}}}(\kern0.7pt y )$, the phase factor of the integrand for
${\hat f_{{M}}}(\kern0.7pt y )$, the phase factor of the integrand for ![]() $\hat \xi _g^+$ in (4.13) is
$\hat \xi _g^+$ in (4.13) is ![]() ${\exp ({\mathrm {i}\int ^y {({k_g} - {k_f})\,\mathrm {d}\,x'} })}$. Applying integration by parts utilising this phase factor once and combining with the Reference Longuet-Higgins and StewartLHS62 solution (3.29) reduces
${\exp ({\mathrm {i}\int ^y {({k_g} - {k_f})\,\mathrm {d}\,x'} })}$. Applying integration by parts utilising this phase factor once and combining with the Reference Longuet-Higgins and StewartLHS62 solution (3.29) reduces ![]() $\hat \xi _g^+$ in (4.13) to
$\hat \xi _g^+$ in (4.13) to
 \begin{equation} \hat \xi _g^+ \left( x \right) = \left[ {{{\hat \xi }_{{{LHS62}}}}\left( x \right) - {{\hat \xi }_{{{LHS62}}}}\left( a \right)\frac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left( a \right)}}} \right]\left[ {1 + O\left( \beta \right)} \right] + \int_a^x {{{\hat \sigma }_{{r}}}\left(\kern0.7pt y \right)} \frac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y, \end{equation}
\begin{equation} \hat \xi _g^+ \left( x \right) = \left[ {{{\hat \xi }_{{{LHS62}}}}\left( x \right) - {{\hat \xi }_{{{LHS62}}}}\left( a \right)\frac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left( a \right)}}} \right]\left[ {1 + O\left( \beta \right)} \right] + \int_a^x {{{\hat \sigma }_{{r}}}\left(\kern0.7pt y \right)} \frac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y, \end{equation}
where the term in the first square brackets ![]() $\hat {\xi }_{{LHS62}}(a) \hat {\xi }_{h}^{+}(x) / \hat {\xi }_{h}^{+}(a)$ appears due to boundary condition
$\hat {\xi }_{{LHS62}}(a) \hat {\xi }_{h}^{+}(x) / \hat {\xi }_{h}^{+}(a)$ appears due to boundary condition ![]() $\hat \xi _g^+ ( a ) = 0$ and the residual source field
$\hat \xi _g^+ ( a ) = 0$ and the residual source field ![]() $\hat \sigma _{{r}}$ due to the subtraction of the Reference Longuet-Higgins and StewartLHS62 solution is
$\hat \sigma _{{r}}$ due to the subtraction of the Reference Longuet-Higgins and StewartLHS62 solution is
 \begin{equation} {\hat \sigma _{{r}}} = \left\{ {\frac{{{k_g} + {k_f}}}{{2{k_f}}}\frac{{\mathrm{d}\left| {{{\hat \xi }_{{{LHS62}}}}} \right|}}{{\mathrm{d}\,x}} + \frac{{\left| {{{\hat \xi }_{{{LHS62}}}}} \right|}}{{2{k_f}h}}\frac{{\mathrm{d}( {{k_g}h} )}}{{\mathrm{d}\,x}}\left[ {1 + O\left( \beta \right)} \right]} \right\}\frac{{\hat S}}{{\left| {\hat S} \right|}}, \end{equation}
\begin{equation} {\hat \sigma _{{r}}} = \left\{ {\frac{{{k_g} + {k_f}}}{{2{k_f}}}\frac{{\mathrm{d}\left| {{{\hat \xi }_{{{LHS62}}}}} \right|}}{{\mathrm{d}\,x}} + \frac{{\left| {{{\hat \xi }_{{{LHS62}}}}} \right|}}{{2{k_f}h}}\frac{{\mathrm{d}( {{k_g}h} )}}{{\mathrm{d}\,x}}\left[ {1 + O\left( \beta \right)} \right]} \right\}\frac{{\hat S}}{{\left| {\hat S} \right|}}, \end{equation}
which is the same as ![]() $\hat \sigma _{{{CLHRDS21}}}$ in (4.18) at leading order.
$\hat \sigma _{{{CLHRDS21}}}$ in (4.18) at leading order.
The present unified solution of group-induced subharmonic (3.11) reduces to the existing solutions as summarised in figure 7.

Figure 7. The present generalised solution based on Green's function (3.15) of group-induced subharmonic reduces to the solution over a flat bottom (Longuet-Higgins & Stewart Reference Longuet-Higgins and Stewart1962), a variable bottom (Zou Reference Zou2011) at off-resonant condition of intermediate water, a variable bottom at near-resonant condition of shallow water (Janssen et al. Reference Janssen, Battjes and van Dongeren2003; Contardo et al. Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and Symonds2021; Liao et al. Reference Liao, Li, Liu and Zou2021) and over a plane beach (Van Leeuwen Reference Van Leeuwen1992; Schäffer Reference Schäffer1993). Here ![]() $k_g=\omega _g/c_g$ and
$k_g=\omega _g/c_g$ and ![]() $k_f= \omega _g / \sqrt {gh}$ are the wavenumber of the wave group and free subharmonic propagating at the speed of shallow-water wave;
$k_f= \omega _g / \sqrt {gh}$ are the wavenumber of the wave group and free subharmonic propagating at the speed of shallow-water wave; ![]() $\mu = 1 - k_f^2/k_g^2$ is the degree of departure from resonance; and
$\mu = 1 - k_f^2/k_g^2$ is the degree of departure from resonance; and ![]() $\hat \xi _h^+ ( x )$ and
$\hat \xi _h^+ ( x )$ and ![]() $\hat \xi _h^- ( x )$ are the linearly independent homogeneous solutions of (2.16) that describe the downwave- and upwave-propagating free subharmonics, respectively.
$\hat \xi _h^- ( x )$ are the linearly independent homogeneous solutions of (2.16) that describe the downwave- and upwave-propagating free subharmonics, respectively.
5. Effect of moving-breakpoint forcing
As long as the forcing term ![]() $\hat f$ for breaking waves can be theoretically pre-described, the present solution of group-induced subharmonic (3.11) can, in principle, be applied to the surf zone, assuming negligible nonlinearity of the subharmonic so that the linearised shallow-water equation is valid. As the first step, the present solution is combined with the seminal moving-breakpoint forcing model (Symonds et al. Reference Symonds, Huntley and Bowen1982; Schäffer Reference Schäffer1993; Contardo & Symonds Reference Contardo and Symonds2016). The sum of downwave and upwave components instead of individual components was solved in previous moving-breakpoint models. In contrast, these two components are independently described in the present model; therefore, the spatial evolution of the downwave component in the excursion region of moving breakpoint can be examined.
$\hat f$ for breaking waves can be theoretically pre-described, the present solution of group-induced subharmonic (3.11) can, in principle, be applied to the surf zone, assuming negligible nonlinearity of the subharmonic so that the linearised shallow-water equation is valid. As the first step, the present solution is combined with the seminal moving-breakpoint forcing model (Symonds et al. Reference Symonds, Huntley and Bowen1982; Schäffer Reference Schäffer1993; Contardo & Symonds Reference Contardo and Symonds2016). The sum of downwave and upwave components instead of individual components was solved in previous moving-breakpoint models. In contrast, these two components are independently described in the present model; therefore, the spatial evolution of the downwave component in the excursion region of moving breakpoint can be examined.
In the surf zone , the energy conservation equation (2.7) and the corresponding radiation stress solution (2.10)–(2.11) are no longer valid due to significant breaking-induced dissipation. Following Schäffer (Reference Schäffer1993), we consider weakly modulated bichromatic wave groups (modulation rate ![]() $\delta =A_2/A_1\ll 1$ is the ratio of amplitudes of two components of bichromatic waves) normally incident onto a plane sloping bottom (figure 8). Let
$\delta =A_2/A_1\ll 1$ is the ratio of amplitudes of two components of bichromatic waves) normally incident onto a plane sloping bottom (figure 8). Let ![]() ${x_a}$ and
${x_a}$ and ![]() ${x_c}$ be the horizontal coordinates of the boundaries of the moving-breakpoint region B in figure 8, and the groupiness is assumed to vanish shoreward of region B. At
${x_c}$ be the horizontal coordinates of the boundaries of the moving-breakpoint region B in figure 8, and the groupiness is assumed to vanish shoreward of region B. At ![]() $x_c$, waves with the maximum amplitude
$x_c$, waves with the maximum amplitude ![]() $A_1( {1 + \delta } )$ start to break, i.e.
$A_1( {1 + \delta } )$ start to break, i.e.
where ![]() $\gamma =\textrm {significant wave height/depth}$ at breakpoint is the breaker index that ranges between 0.5 and 1 (Goda Reference Goda2010). Similarly, at
$\gamma =\textrm {significant wave height/depth}$ at breakpoint is the breaker index that ranges between 0.5 and 1 (Goda Reference Goda2010). Similarly, at ![]() $x_a$, waves with the minimum amplitude
$x_a$, waves with the minimum amplitude ![]() $A_1( 1 - \delta )$ start to break, i.e.
$A_1( 1 - \delta )$ start to break, i.e.

Figure 8. Sketch of bottom topography and spatial variation of the amplitude of bichromatic waves normally incident on a plane sloping bottom. Positions ![]() $x_a$,
$x_a$, ![]() $x_m$ and
$x_m$ and ![]() $x_c$ are where waves with the minimum, mean and maximum amplitude break. Reproduced from figure 3 in Schäffer (Reference Schäffer1993).
$x_c$ are where waves with the minimum, mean and maximum amplitude break. Reproduced from figure 3 in Schäffer (Reference Schäffer1993).
The steady components of radiation stress in the surf zone and shoaling zone indicated by regions I and II in figure 8 are
To leading order of ![]() $O( \delta )$, Schäffer (Reference Schäffer1993) derived the complex amplitude of the radiation stress gradient oscillating with group frequency in the moving-breakpoint region B:
$O( \delta )$, Schäffer (Reference Schäffer1993) derived the complex amplitude of the radiation stress gradient oscillating with group frequency in the moving-breakpoint region B:
where ![]() $0 \leq \tau ( x ) \leq {\rm \pi}$ denotes the group phase when wave breaking ceases and is given by
$0 \leq \tau ( x ) \leq {\rm \pi}$ denotes the group phase when wave breaking ceases and is given by
The spatial evolution of ![]() $A_1$ and
$A_1$ and ![]() $A_2$ during energy conservative shoaling can be solved from (2.8a,b) as
$A_2$ during energy conservative shoaling can be solved from (2.8a,b) as
 \begin{equation} \frac{A_1(x)}{A_1(x_a)} = \frac{A_2(x)}{A_2(x_a)} = \sqrt{\frac{c_g(x_a)}{c_g(x)}}, \end{equation}
\begin{equation} \frac{A_1(x)}{A_1(x_a)} = \frac{A_2(x)}{A_2(x_a)} = \sqrt{\frac{c_g(x_a)}{c_g(x)}}, \end{equation}
and therefore ![]() $\delta =A_2/A_1$ remains spatially invariant.
$\delta =A_2/A_1$ remains spatially invariant.
Substituting (5.1) and (5.2) into (5.5) yields ![]() $\tau ( {{x_a}} ) = {\rm \pi}$ and
$\tau ( {{x_a}} ) = {\rm \pi}$ and ![]() $\tau ( {{x_c}} ) = 0$. In addition, at
$\tau ( {{x_c}} ) = 0$. In addition, at ![]() $x = {x_m}$ where the primary component of the bichromatic wave breaks, we have
$x = {x_m}$ where the primary component of the bichromatic wave breaks, we have ![]() $2\sqrt {2}{A_1}( {{x_m}} ) = \gamma h( {{x_m}} )$ and
$2\sqrt {2}{A_1}( {{x_m}} ) = \gamma h( {{x_m}} )$ and ![]() $\tau (x_{m})={\rm \pi} / 2$ according to (5.5).
$\tau (x_{m})={\rm \pi} / 2$ according to (5.5).
The derivative of (5.4) gives the forcing term for governing equation of the subharmonic:
where ![]() $\mathrm {d}\tau /\mathrm {d}\,x$ can be obtained from the derivatives of (5.5) and (5.6):
$\mathrm {d}\tau /\mathrm {d}\,x$ can be obtained from the derivatives of (5.5) and (5.6):
Positive and negative ![]() $\mathrm {d}^{2} \hat {S}^{({B})} / \mathrm {d}\,x^{2}$ indicate the forcing term is in phase or antiphase with the wave group at
$\mathrm {d}^{2} \hat {S}^{({B})} / \mathrm {d}\,x^{2}$ indicate the forcing term is in phase or antiphase with the wave group at ![]() ${x_c}$, because the excursion of region B was small, and the group phase variation was neglected.
${x_c}$, because the excursion of region B was small, and the group phase variation was neglected.
Substituting the shallow-water approximation ![]() $c_g\approx c\approx \sqrt {gh}$ and (5.8) into (5.7) yields
$c_g\approx c\approx \sqrt {gh}$ and (5.8) into (5.7) yields
 \begin{equation} \frac{8{\rm \pi} }{{3\rho
g{\gamma ^2}h_x^2}}\frac{{{\mathrm{d}^2}\hat
S_1^{({{B}})}}}{{\mathrm{d}\,{x^2}}} = \Biggl[ {1 -
3{{\left( {\frac{{{A_1}}}{{\gamma h}}} \right)}^2}}
\Biggr]\sin \tau + \frac{5\sqrt{2}}{16}\frac{{\gamma
h}}{{{A_1}\delta }}\Biggl[ {1 + 2{{\left(
{\frac{{{A_1}}}{{\gamma h}}} \right)}^2}} \Biggr]\left( { -
\cot \tau } \right). \end{equation}
\begin{equation} \frac{8{\rm \pi} }{{3\rho
g{\gamma ^2}h_x^2}}\frac{{{\mathrm{d}^2}\hat
S_1^{({{B}})}}}{{\mathrm{d}\,{x^2}}} = \Biggl[ {1 -
3{{\left( {\frac{{{A_1}}}{{\gamma h}}} \right)}^2}}
\Biggr]\sin \tau + \frac{5\sqrt{2}}{16}\frac{{\gamma
h}}{{{A_1}\delta }}\Biggl[ {1 + 2{{\left(
{\frac{{{A_1}}}{{\gamma h}}} \right)}^2}} \Biggr]\left( { -
\cot \tau } \right). \end{equation}
The second term on the right-hand side in (5.9) is of leading order ![]() $O({\delta ^{ - 1}})$, thus determining the sign of
$O({\delta ^{ - 1}})$, thus determining the sign of ![]() $\mathrm {d}^{2} \hat {S}^{({B})} / \mathrm {d}\,x^{2}$. In the outer half of region B (
$\mathrm {d}^{2} \hat {S}^{({B})} / \mathrm {d}\,x^{2}$. In the outer half of region B (![]() ${x_m} < x < {x_c}$),
${x_m} < x < {x_c}$), ![]() $0 < \tau <{\rm \pi} /2$ and
$0 < \tau <{\rm \pi} /2$ and ![]() $- \cot \tau < 0$, hence
$- \cot \tau < 0$, hence ![]() $\mathrm {d}^{2} \hat {S}^{({B})} / \mathrm {d}\,x^{2} < 0$; in the inner half (
$\mathrm {d}^{2} \hat {S}^{({B})} / \mathrm {d}\,x^{2} < 0$; in the inner half (![]() ${x_a} < x < {x_m}$),
${x_a} < x < {x_m}$), ![]() ${\rm \pi} /2<\tau <{\rm \pi}$ and
${\rm \pi} /2<\tau <{\rm \pi}$ and ![]() $- \cot \tau > 0$, hence
$- \cot \tau > 0$, hence ![]() $\mathrm {d}^{2} \hat {S}^{({B})} / \mathrm {d}\,x^{2}> 0$. According to (3.34), at leading order,
$\mathrm {d}^{2} \hat {S}^{({B})} / \mathrm {d}\,x^{2}> 0$. According to (3.34), at leading order, ![]() $\mathrm {d}^2\hat S/\mathrm {d}\,x^2$ prior to breaking is in antiphase with the wave group, and the above result indicates that the opposite is true once wave groups pass
$\mathrm {d}^2\hat S/\mathrm {d}\,x^2$ prior to breaking is in antiphase with the wave group, and the above result indicates that the opposite is true once wave groups pass ![]() ${x_m}$. Therefore, the subharmonic locally generated in region B (
${x_m}$. Therefore, the subharmonic locally generated in region B (![]() $\hat \xi _{( {{B}} )}^+$) interferes with the subharmonic entering region B constructively seaward of
$\hat \xi _{( {{B}} )}^+$) interferes with the subharmonic entering region B constructively seaward of ![]() ${x_m}$, but destructively shoreward of
${x_m}$, but destructively shoreward of ![]() ${x_m}$ (figure 9).
${x_m}$ (figure 9).

Figure 9. Diagram of phase difference between the downwave-propagating subharmonic (![]() $\hat \xi _g^+$) entering the moving-breakpoint region B in figure 8 at
$\hat \xi _g^+$) entering the moving-breakpoint region B in figure 8 at ![]() $x=x_c$ and the downwave component generated in region B (
$x=x_c$ and the downwave component generated in region B (![]() $\hat \xi _{( {{B}} )}^+$). Here
$\hat \xi _{( {{B}} )}^+$). Here ![]() $\Delta \varphi \leq {\rm \pi}/ 2$ denotes a certain phase lag between
$\Delta \varphi \leq {\rm \pi}/ 2$ denotes a certain phase lag between ![]() $\hat \xi _g^+ ( {{x_c}} )$ and radiation stress in addition to
$\hat \xi _g^+ ( {{x_c}} )$ and radiation stress in addition to ![]() ${\rm \pi}$, which is developed during shoaling prior to breaking.
${\rm \pi}$, which is developed during shoaling prior to breaking.
The overall effect of group forcing in region B depends on the spatial variation of the source field magnitude. Substituting (5.9) into (3.2), (3.36) and (3.7), the source field in region B, ![]() $\hat \sigma ^{({\rm B})}$, is given by
$\hat \sigma ^{({\rm B})}$, is given by
 \begin{equation} \frac{{64{\rm \pi} }}{{15\mathrm{i}h_x^2}}{\hat \sigma ^{({{B}})}} = \frac{{{\gamma ^2}}}{\delta }\frac{1}{{{k_f}h}}\left( {\frac{{\gamma h}}{{2\sqrt{2}{A_1}}} + \frac{1}{4}\frac{{2\sqrt{2}{A_1}}}{{\gamma h}}} \right)\left( { - \cot \tau } \right) + O\left( 1 \right). \end{equation}
\begin{equation} \frac{{64{\rm \pi} }}{{15\mathrm{i}h_x^2}}{\hat \sigma ^{({{B}})}} = \frac{{{\gamma ^2}}}{\delta }\frac{1}{{{k_f}h}}\left( {\frac{{\gamma h}}{{2\sqrt{2}{A_1}}} + \frac{1}{4}\frac{{2\sqrt{2}{A_1}}}{{\gamma h}}} \right)\left( { - \cot \tau } \right) + O\left( 1 \right). \end{equation}
Given that ![]() $A_1 \propto c_g^{-0.5} \propto h^{ - 1/4}$ (5.6) and
$A_1 \propto c_g^{-0.5} \propto h^{ - 1/4}$ (5.6) and ![]() $2\sqrt {2}A_1( x_m ) = \gamma h( {{x_m}} )$, the coefficient of
$2\sqrt {2}A_1( x_m ) = \gamma h( {{x_m}} )$, the coefficient of ![]() $- \cot \tau$ in the above equation reduces to
$- \cot \tau$ in the above equation reduces to
 \begin{equation} \frac{1}{k_{f} h}\left(\frac{\gamma h}{2\sqrt{2}A_{1}}+\frac{1}{4} \frac{2\sqrt{2}A_{1}}{\gamma h}\right)=\frac{1}{\omega_{g}} \sqrt{\frac{g}{h\left(x_{m}\right)}}\left\{\left[\frac{h}{h\left(x_{m}\right)}\right]^{3 / 4}+\frac{1}{4}\left[\frac{h}{h\left(x_{m}\right)}\right]^{{-}7 / 4}\right\} . \end{equation}
\begin{equation} \frac{1}{k_{f} h}\left(\frac{\gamma h}{2\sqrt{2}A_{1}}+\frac{1}{4} \frac{2\sqrt{2}A_{1}}{\gamma h}\right)=\frac{1}{\omega_{g}} \sqrt{\frac{g}{h\left(x_{m}\right)}}\left\{\left[\frac{h}{h\left(x_{m}\right)}\right]^{3 / 4}+\frac{1}{4}\left[\frac{h}{h\left(x_{m}\right)}\right]^{{-}7 / 4}\right\} . \end{equation}
Because ![]() $\gamma h / (2\sqrt {2}A_{1})=[A_{1}(x_{m}) / h(x_{m})] /(A_{1} / h)=[h / h(x_{m})]^{5 / 4}$ and
$\gamma h / (2\sqrt {2}A_{1})=[A_{1}(x_{m}) / h(x_{m})] /(A_{1} / h)=[h / h(x_{m})]^{5 / 4}$ and ![]() $\gamma h \geqslant 2\sqrt {2}{A_1} ( {1 - \delta } )$, for
$\gamma h \geqslant 2\sqrt {2}{A_1} ( {1 - \delta } )$, for ![]() $\delta < 0.23$, we have
$\delta < 0.23$, we have ![]() $h / h(x_{m}) =(\gamma h / 2\sqrt {2}A_{1})^{4 / 5} \geq (1-\delta )^{4 / 5}>0.81$ and (5.11) decreases with decreasing depth. Thus the source field
$h / h(x_{m}) =(\gamma h / 2\sqrt {2}A_{1})^{4 / 5} \geq (1-\delta )^{4 / 5}>0.81$ and (5.11) decreases with decreasing depth. Thus the source field ![]() $\hat \sigma ^{({\rm B})}$ is stronger in the outer than in the inner half of region B; therefore, the downwave subharmonic is slightly enhanced over region B.
$\hat \sigma ^{({\rm B})}$ is stronger in the outer than in the inner half of region B; therefore, the downwave subharmonic is slightly enhanced over region B.
As an example of applying the present solution to the moving-breakpoint forcing model, the present solution shown in figure 6 is re-calculated here with the forcing term in region B replaced by ![]() $\mathrm {d}^{2} \hat {S}^{({B})} / \mathrm {d}\,x^{2}$ in (5.7) and the results are shown as dashed lines in figure 10 (see Appendix B for details of calculation). Note that
$\mathrm {d}^{2} \hat {S}^{({B})} / \mathrm {d}\,x^{2}$ in (5.7) and the results are shown as dashed lines in figure 10 (see Appendix B for details of calculation). Note that ![]() $\hat \xi _g^-(x)$ in region shoreward of
$\hat \xi _g^-(x)$ in region shoreward of ![]() $x_a$ is set to zero because the present model assumes zero groupiness and hence zero group forcing in this region; therefore theoretically no upwave-propagating component of group-induced subharmonic exists. For the same reason, no phase lag was calculated shoreward of
$x_a$ is set to zero because the present model assumes zero groupiness and hence zero group forcing in this region; therefore theoretically no upwave-propagating component of group-induced subharmonic exists. For the same reason, no phase lag was calculated shoreward of ![]() $x_a$ where there is no wave group.
$x_a$ where there is no wave group.

Figure 10. Amplitude (a,b) and phase (c,d) of the complex amplitude ![]() $\hat \xi (x)$ of the subharmonic surface elevation
$\hat \xi (x)$ of the subharmonic surface elevation ![]() $\tilde {\xi }(x,t)$ induced by bichromatic wave groups normally incident over a plane sloping bottom. Weakly modulated test case A-4 (a,c) and strongly modulated test case B-5 (b,d) of the flume experiment of Van Noorloos (Reference Van Noorloos2003). Laboratory measurements (circles), the present solution for non-breaking wave
$\tilde {\xi }(x,t)$ induced by bichromatic wave groups normally incident over a plane sloping bottom. Weakly modulated test case A-4 (a,c) and strongly modulated test case B-5 (b,d) of the flume experiment of Van Noorloos (Reference Van Noorloos2003). Laboratory measurements (circles), the present solution for non-breaking wave ![]() $\hat \xi =\hat \xi _g^+ + \hat \xi _{sc} + \hat \xi _g^-$ where
$\hat \xi =\hat \xi _g^+ + \hat \xi _{sc} + \hat \xi _g^-$ where ![]() $\hat \xi _{sc}$ denotes the downwave free subharmonic generated due to scattering at the slope toe ((B11), black solid lines) and its downwave- and upwave-propagating group-induced subharmonic components,
$\hat \xi _{sc}$ denotes the downwave free subharmonic generated due to scattering at the slope toe ((B11), black solid lines) and its downwave- and upwave-propagating group-induced subharmonic components, ![]() $\hat \xi _g^+$ (blue solid lines) and
$\hat \xi _g^+$ (blue solid lines) and ![]() $\hat \xi _g^-$ (red solid lines) in (B13). The counterpart solution combined with moving-breakpoint forcing model for breaking waves is shown as dashed lines. The yellow shaded area denotes the moving breakpoint within
$\hat \xi _g^-$ (red solid lines) in (B13). The counterpart solution combined with moving-breakpoint forcing model for breaking waves is shown as dashed lines. The yellow shaded area denotes the moving breakpoint within ![]() $[x_a,x_c]$. Phase is the phase lag behind wave groups plus
$[x_a,x_c]$. Phase is the phase lag behind wave groups plus ![]() ${\rm \pi}$. Note that in (b), the phase of the upwave component
${\rm \pi}$. Note that in (b), the phase of the upwave component ![]() $\hat {\xi }_g^-$ was manually shifted by
$\hat {\xi }_g^-$ was manually shifted by ![]() ${\rm \pi}$ for plotting purposes.
${\rm \pi}$ for plotting purposes.
In both the weakly and strongly modulated test cases, the present solution predicts the spatial variation of the subharmonic amplitude to be in good agreement with observation, despite that the model was developed for weak modulation initially. As the water depth decreases, the predicted amplitude of the downwave-propagating subharmonic in test A-4 first increases in the outer half of the moving-breakpoint region and then decreases in the inner half by almost the same amount. The trend of the spatial evolution of amplitude is consistent with the analysis above for (5.9) in the case of the weak modulation in test A-4. For the strong modulation case of test B-5, the amplitude of the downwave-propagating component keeps increasing in the moving-breakpoint region. The predicted phase lag between the subharmonic and group deviates from observation in the moving-breakpoint region, possibly due to growing discrepancy between theoretical predictions of the wave group and observations in the surf zone. It is well known that wave groupiness is subject to drastic change after wave breaking, possibly due to greater decay of higher waves (Svendsen & Veeramony Reference Svendsen and Veeramony2001) or the modulation of breaking water depth by group-induced subharmonics (Janssen et al. Reference Janssen, Battjes and van Dongeren2003; Liu & Li Reference Liu and Li2018). Accurate estimation of the wave group phase from observations inside the surf zone would improve the prediction of phase lag. Albeit minor compared to the breaking effect, partial reflections of downwave-propagating components may also be included to further improve the accuracy of theoretical predictions (Contardo et al. Reference Contardo, Lowe, Dufois, Hansen, Buckley and Symonds2023).
6. Future work
The exact form of the solution (3.11) directly relies on the spectral expression for the radiation stress, which is not well established for irregular waves in the surf zone. For bichromatic waves, (2.1) combined with the concept of breaker index results in the steady component of radiation stress solution in the surf zone ![]() ${\bar S^{( {{I}} )}}$ in (5.3a) used in the moving-breakpoint forcing model. This approach does not account for the effect of surface rollers, and therefore can be erroneous. For instance, for plunging-type wave breaking, there is little change in the radiation stress between the breakpoint and the plunge point (Bowen, Inman & Simmons Reference Bowen, Inman and Simmons1968), indicating that the radiation stress in the outer surf zone does not decrease with depth as quickly as what is predicted by
${\bar S^{( {{I}} )}}$ in (5.3a) used in the moving-breakpoint forcing model. This approach does not account for the effect of surface rollers, and therefore can be erroneous. For instance, for plunging-type wave breaking, there is little change in the radiation stress between the breakpoint and the plunge point (Bowen, Inman & Simmons Reference Bowen, Inman and Simmons1968), indicating that the radiation stress in the outer surf zone does not decrease with depth as quickly as what is predicted by ![]() $\bar S^{( {I} )} \propto h^2$ in (5.3a,b). Accordingly,
$\bar S^{( {I} )} \propto h^2$ in (5.3a,b). Accordingly, ![]() $\mathrm {d}\bar S^{(I)}/\mathrm {d}\,x$ in (5.7) can be overestimated, as can the growth of downwave-propagating subharmonic in the outer half of the moving-breakpoint region. Similarly, Rijnsdorp, Smit & Zijlema (Reference Rijnsdorp, Smit and Zijlema2014) found that a non-hydrostatic model incapable of reproducing surface rollers tends to over-predict the amplitude of the subharmonic in the moving-breakpoint region. Zou et al. (Reference Zou, Bowen and Hay2006) derived a generalised analytical solution for the vertical distribution of wave radiation stress in the presence of bottom slope, bottom friction and depth-induced wave breaking in the shoaling region and surf zone and conducted field observations to verify the theory. The cross-shore evolution of wave energy is described by the wave energy flux conservation equation including dissipation due to bottom friction and breaking in analogy with a travelling bore as in Thornton & Guza (Reference Thornton and Guza1983). Existing models that account for the surface roller effect, such as those of Svendsen (Reference Svendsen1984) and Dally & Brown (Reference Dally and Brown1995), only consider the steady component of radiation stress that is not responsible for driving the subharmonic. Moreover, despite some efforts (e.g. Reniers et al. Reference Reniers, van Dongeren, Battjes and Thornton2002; Contardo & Symonds Reference Contardo and Symonds2016), the extension of the spectral expression of radiation stress from bichromatic to irregular wave groups in the surf zone is not as straightforward as it is for non-breaking waves. Future work of spectral expression of radiation stress for realistic irregular waves in the surf zone is needed, based on high-resolution datasets of velocity profiles from numerical or physical experiments, as per Ting & Kirby (Reference Ting and Kirby1994), Chang & Liu (Reference Chang and Liu1999), Lin & Liu (Reference Lin and Liu1998), Wang, Zou & Reeve (Reference Wang, Zou and Reeve2009), Kimmoun & Branger (Reference Kimmoun and Branger2007), Bakhtyar et al. (Reference Bakhtyar, Razmi, Barry, Yeganeh-Bakhtiary and Zou2010), Pedrozo-Acuña et al. (Reference Pedrozo-Acuña, Torres-Freyermuth, Zou, Hsu and Reeve2010), Ruju, Lara & Losada (Reference Ruju, Lara and Losada2012), Na, Chang & Lim (Reference Na, Chang and Lim2020) and Xie & Lin (Reference Xie and Lin2022).
$\mathrm {d}\bar S^{(I)}/\mathrm {d}\,x$ in (5.7) can be overestimated, as can the growth of downwave-propagating subharmonic in the outer half of the moving-breakpoint region. Similarly, Rijnsdorp, Smit & Zijlema (Reference Rijnsdorp, Smit and Zijlema2014) found that a non-hydrostatic model incapable of reproducing surface rollers tends to over-predict the amplitude of the subharmonic in the moving-breakpoint region. Zou et al. (Reference Zou, Bowen and Hay2006) derived a generalised analytical solution for the vertical distribution of wave radiation stress in the presence of bottom slope, bottom friction and depth-induced wave breaking in the shoaling region and surf zone and conducted field observations to verify the theory. The cross-shore evolution of wave energy is described by the wave energy flux conservation equation including dissipation due to bottom friction and breaking in analogy with a travelling bore as in Thornton & Guza (Reference Thornton and Guza1983). Existing models that account for the surface roller effect, such as those of Svendsen (Reference Svendsen1984) and Dally & Brown (Reference Dally and Brown1995), only consider the steady component of radiation stress that is not responsible for driving the subharmonic. Moreover, despite some efforts (e.g. Reniers et al. Reference Reniers, van Dongeren, Battjes and Thornton2002; Contardo & Symonds Reference Contardo and Symonds2016), the extension of the spectral expression of radiation stress from bichromatic to irregular wave groups in the surf zone is not as straightforward as it is for non-breaking waves. Future work of spectral expression of radiation stress for realistic irregular waves in the surf zone is needed, based on high-resolution datasets of velocity profiles from numerical or physical experiments, as per Ting & Kirby (Reference Ting and Kirby1994), Chang & Liu (Reference Chang and Liu1999), Lin & Liu (Reference Lin and Liu1998), Wang, Zou & Reeve (Reference Wang, Zou and Reeve2009), Kimmoun & Branger (Reference Kimmoun and Branger2007), Bakhtyar et al. (Reference Bakhtyar, Razmi, Barry, Yeganeh-Bakhtiary and Zou2010), Pedrozo-Acuña et al. (Reference Pedrozo-Acuña, Torres-Freyermuth, Zou, Hsu and Reeve2010), Ruju, Lara & Losada (Reference Ruju, Lara and Losada2012), Na, Chang & Lim (Reference Na, Chang and Lim2020) and Xie & Lin (Reference Xie and Lin2022).
In the present theoretical study, the linearised shallow-water equation is used in combination with the moving-breakpoint forcing model for the surf zone. It is necessary to adopt the fully nonlinear shallow-water equation in the nearshore region near the shoreline, where the self-interaction of the subharmonic may lead to energy dissipation in the infragravity band by transferring energy back to the short-wave band (De Bakker et al. Reference De Bakker, Herbers, Smit, Tissier and Ruessink2015, Reference De Bakker, Tissier and Ruessink2016) or even by breaking (Van Dongeren et al. Reference Van Dongeren, Battjes, Janssen, Van Noorloos, Steenhauer, Steenbergen and Reniers2007). Moreover, subharmonics may also gain energy in the inner surf zone through bore merging by modulating the celerity of individual bores (Bonneton & Dupuis Reference Bonneton and Dupuis2001; Sénéchal et al. Reference Sénéchal, Dupuis, Bonneton, Howa and Pedreros2001; Tissier et al. Reference Tissier, Bonneton, Michallet and Ruessink2015), which is highly nonlinear.
The present Green's function-based solution has the potential advantage for practical application in that the Green's function for a certain area is only a function of the whole topography within that area regardless of wave conditions. The local Green's function can be extracted from in situ datasets through data-driven deep learning (Gin et al. Reference Gin, Shea, Brunton and Kutz2021; Boullé, Earls & Townsend Reference Boullé, Earls and Townsend2022) and then used for fast forecasts for any incident wave conditions and group forcing. Furthermore, the forcing term (3.2) can be extended to account for forcing factors other than radiation stress in governing equation (2.16) and then substituted into (3.4).
The present 1-D solution can be extended to two-dimensional wave fields by incorporating two-dimensional radiation stress and replacing the present Green's function for the 1-D shallow-water equation with the two-dimensional counterpart.
7. Conclusions
The unified solution for wave-group-induced subharmonics is derived based on Green's function, which allows for a new physical interpretation of the generation and formation of the subharmonic. The group-forcing field is divided into successive time-dependent pulses in space. The group-induced subharmonic is the superposition of all the free subharmonics generated by each group-forcing pulse, which is bound to the wave group through the group forcing related to wave radiation stress, so-called bound subharmonic infragravity wave in previous studies. The present solution reduces to the existing solutions for the off-resonance condition at intermediate water (Longuet-Higgins & Stewart Reference Longuet-Higgins and Stewart1962; Zou Reference Zou2011) and the near-resonance condition at shallow water and a plane beach (Van Leeuwen Reference Van Leeuwen1992; Schäffer Reference Schäffer1993; Janssen et al. Reference Janssen, Battjes and van Dongeren2003; Contardo et al. Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and Symonds2021; Liao et al. Reference Liao, Li, Liu and Zou2021). The underlying mechanism of the transition between bound and free subharmonics is elucidated consistently from intermediate to shallow water.
The solution based on Green's function indicates that, under the local forcing of radiation stress gradient, two subharmonics keep radiating away from the source location regardless of depth gradient considered in Contardo et al. (Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and Symonds2021). As a result, downwave- and upwave-propagating subharmonic components are generated at the upwave and downwave side of any observation position. Thus, the group-induced subharmonic is dependent on the entire topography surrounding the observation position. The integrated historic topographic effect may not be significant for the off-resonance condition at intermediate water due to destructive interference among subharmonic components, but becomes significant for the downwave-propagating component for the near-resonance condition at shallow water due to constructive interference among subharmonic components.
For mildly sloping uneven bottoms, at leading order, each subharmonic is initially ahead of wave groups by ![]() ${\rm \pi} /2$. For full resonance condition in shallow water, the phase difference of
${\rm \pi} /2$. For full resonance condition in shallow water, the phase difference of ![]() ${\rm \pi} /2$ between downwave-propagating subharmonic and wave groups remains invariant during propagation due to the same propagating speed; thereby all the downwave-propagating subharmonics interfere with each other constructively. Consequently, the superposed downwave-propagating subharmonic leads wave groups by
${\rm \pi} /2$ between downwave-propagating subharmonic and wave groups remains invariant during propagation due to the same propagating speed; thereby all the downwave-propagating subharmonics interfere with each other constructively. Consequently, the superposed downwave-propagating subharmonic leads wave groups by ![]() ${\rm \pi} /2$, and its amplitude increases with travel distance of wave groups. Moreover, under this condition, the bound subharmonic is theoretically indistinguishable from the free subharmonic in the downwave-propagating subharmonic (3.30), which can be interpreted as its release. However, the opposite is true for the upwave-propagating subharmonic since resonance does not occur in the upwave direction.
${\rm \pi} /2$, and its amplitude increases with travel distance of wave groups. Moreover, under this condition, the bound subharmonic is theoretically indistinguishable from the free subharmonic in the downwave-propagating subharmonic (3.30), which can be interpreted as its release. However, the opposite is true for the upwave-propagating subharmonic since resonance does not occur in the upwave direction.
For bichromatic waves normally incident on a plane beach, the amplitude of group-induced subharmonic in the moving-breakpoint region predicted by the Green's function-based solution is consistent with previous laboratory observations. For weakly modulated waves, the solution indicates that the amplitude of the downwave-propagating component increases and decreases in the outer and inner half of the moving-breakpoint region. The solution is expected to be applicable to random waves in the surf zone, as long as the spectral expression of the group forcing of breaking waves can be pre-described. This calls for further studies of the temporal and spatial variation of radiation stress in the surf zone.
Supplementary material
The data and codes for generating the figures in the present paper are openly available in Zenodo at http://doi.org/10.5281/zenodo.7813457.
Acknowledgements
This research was initiated when Z.L. was studying for a doctorate in Tianjin University. The authors are grateful to the anonymous reviewers for their comments that greatly improved the manuscript. The authors are grateful to Dr A. van Dongeren for providing the data of the laboratory experiment.
Funding
The first and second authors have been supported by UK Natural Environment Research Council (NERC) grant NE/V006088/1. The third author has been supported by the National Natural Science Foundation of China (grant no. 52201333).
Declaration of interests
The authors report no conflict of interest.
Author contributions
Z.L.: theory derivation and figures; Z.L. and Q.Z.: conceptualisation and methodology; Z.L., Y.L., S.C. and Q.Z.: writing, review and editing; Q.Z. and S.L: supervision and funding.
Appendix A. Error of the solution on slowly varying water depth
The error of the solution for the bound subharmonic ![]() ${\hat \xi _b} = \hat \xi _b^+ + \hat \xi _b^-$ using (3.39) is analysed as follows. The solution (3.39) for
${\hat \xi _b} = \hat \xi _b^+ + \hat \xi _b^-$ using (3.39) is analysed as follows. The solution (3.39) for ![]() $\hat \xi _b^ \pm$ satisfies the following equation:
$\hat \xi _b^ \pm$ satisfies the following equation:
 \begin{equation} \frac{1}{h}\frac{\mathrm{d}}{{\mathrm{d}\,x}}\left( {h\frac{{\mathrm{d}\hat \xi _b^ \pm }}{{\mathrm{d}\,x}}} \right) + k_f^2\hat \xi _b^ \pm= \frac{1}{2}\hat f - \frac{1}{2}{\hat f_{r}} - 0.25\frac{{{h_{xx}}}}{h}\hat \xi _b^ \pm + 0.0625{\left( {\frac{{{h_x}}}{h}} \right)^2}\hat \xi _b^ \pm , \end{equation}
\begin{equation} \frac{1}{h}\frac{\mathrm{d}}{{\mathrm{d}\,x}}\left( {h\frac{{\mathrm{d}\hat \xi _b^ \pm }}{{\mathrm{d}\,x}}} \right) + k_f^2\hat \xi _b^ \pm= \frac{1}{2}\hat f - \frac{1}{2}{\hat f_{r}} - 0.25\frac{{{h_{xx}}}}{h}\hat \xi _b^ \pm + 0.0625{\left( {\frac{{{h_x}}}{h}} \right)^2}\hat \xi _b^ \pm , \end{equation}
where ![]() $\hat {f}_{r}$ is the forcing term of order
$\hat {f}_{r}$ is the forcing term of order ![]() $O(\beta ^2)$ defined in (3.34). Using (A1),
$O(\beta ^2)$ defined in (3.34). Using (A1), ![]() ${\hat \xi _b} = \hat \xi _b^+ + \hat \xi _b^-$ satisfies
${\hat \xi _b} = \hat \xi _b^+ + \hat \xi _b^-$ satisfies
 \begin{equation} \frac{1}{h}\frac{\mathrm{d}}{{\mathrm{d}\,x}}\left( {h\frac{{\mathrm{d}{{\hat \xi }_b}}}{{\mathrm{d}\,x}}} \right) + k_f^2{\hat \xi _b} = \hat f - {\hat f_{r}} - 0.25\frac{{{h_{xx}}}}{h}{\hat \xi _b} + 0.0625{\left( {\frac{{{h_x}}}{h}} \right)^2}{\hat \xi _b}. \end{equation}
\begin{equation} \frac{1}{h}\frac{\mathrm{d}}{{\mathrm{d}\,x}}\left( {h\frac{{\mathrm{d}{{\hat \xi }_b}}}{{\mathrm{d}\,x}}} \right) + k_f^2{\hat \xi _b} = \hat f - {\hat f_{r}} - 0.25\frac{{{h_{xx}}}}{h}{\hat \xi _b} + 0.0625{\left( {\frac{{{h_x}}}{h}} \right)^2}{\hat \xi _b}. \end{equation} Let ![]() ${\hat \xi _{r}}$ be the truncated error between
${\hat \xi _{r}}$ be the truncated error between ![]() ${\hat \xi _b}$ and exact solution, i.e.
${\hat \xi _b}$ and exact solution, i.e.
and subtracting (A2) from (A3) yields
 \begin{equation} \frac{1}{h}\frac{\mathrm{d}}{{\mathrm{d}\,x}}\left( {h\frac{{\mathrm{d}{{\hat \xi }_{r}}}}{{\mathrm{d}\,x}}} \right) + k_f^2{\hat \xi _{r}} = {\hat f_{r}} + 0.25\frac{{{h_{xx}}}}{h}{\hat \xi _b} - 0.0625{\left( {\frac{{{h_x}}}{h}} \right)^2}{\hat \xi _b}. \end{equation}
\begin{equation} \frac{1}{h}\frac{\mathrm{d}}{{\mathrm{d}\,x}}\left( {h\frac{{\mathrm{d}{{\hat \xi }_{r}}}}{{\mathrm{d}\,x}}} \right) + k_f^2{\hat \xi _{r}} = {\hat f_{r}} + 0.25\frac{{{h_{xx}}}}{h}{\hat \xi _b} - 0.0625{\left( {\frac{{{h_x}}}{h}} \right)^2}{\hat \xi _b}. \end{equation}The order of the inhomogeneous term in (A4) is estimated using (3.28) and (3.34) to be
 $$\begin{align}
{{\hat f}_{{r}}} + 0.25\frac{{{h_{xx}}}}{h}{{\hat \xi }_b}
- 0.0625{\left( {\frac{{{h_x}}}{h}} \right)^2}{{\hat \xi
}_b} &= \mu k_g^2{{\hat \xi }_b}O({{\beta ^2}})
+ 0.25k_g^2{{\hat \xi }_b}\frac{{{h_{xx}}}}{{k_g^2h}} -
0.0625k_g^2{{\hat \xi }_b}{\beta ^2} \nonumber\\
&=k_g^2{{\hat \xi }_b}\left( {1 + \mu } \right)O({{\beta ^2}}),
\end{align}$$
$$\begin{align}
{{\hat f}_{{r}}} + 0.25\frac{{{h_{xx}}}}{h}{{\hat \xi }_b}
- 0.0625{\left( {\frac{{{h_x}}}{h}} \right)^2}{{\hat \xi
}_b} &= \mu k_g^2{{\hat \xi }_b}O({{\beta ^2}})
+ 0.25k_g^2{{\hat \xi }_b}\frac{{{h_{xx}}}}{{k_g^2h}} -
0.0625k_g^2{{\hat \xi }_b}{\beta ^2} \nonumber\\
&=k_g^2{{\hat \xi }_b}\left( {1 + \mu } \right)O({{\beta ^2}}),
\end{align}$$and therefore (A4) becomes
 \begin{equation} \frac{1}{h}\frac{\mathrm{d}}{{\mathrm{d}\,x}}\left( {h\frac{{\mathrm{d}{{\hat \xi }_{r}}}}{{\mathrm{d}\,x}}} \right) + k_f^2{\hat \xi _{r}} = k_g^2{\hat \xi _b}\left( {1 + \mu } \right)O( {{\beta ^2}}). \end{equation}
\begin{equation} \frac{1}{h}\frac{\mathrm{d}}{{\mathrm{d}\,x}}\left( {h\frac{{\mathrm{d}{{\hat \xi }_{r}}}}{{\mathrm{d}\,x}}} \right) + k_f^2{\hat \xi _{r}} = k_g^2{\hat \xi _b}\left( {1 + \mu } \right)O( {{\beta ^2}}). \end{equation}
Equation (A6) has the same form as the governing equation (2.16), and the solution (3.28) indicates that ![]() ${\hat \xi _{r}}$ in (A6) is of order
${\hat \xi _{r}}$ in (A6) is of order
 \begin{equation} {\hat \xi _{r}} =
\frac{{k_g^2{{\hat \xi }_b}\left( {1 + \mu }
\right)}}{{k_g^2\mu }}O({{\beta ^2}}) = {\hat
\xi _b}\left( {\frac{1}{\mu } + 1} \right)O( {{\beta ^2}} ), \end{equation}
\begin{equation} {\hat \xi _{r}} =
\frac{{k_g^2{{\hat \xi }_b}\left( {1 + \mu }
\right)}}{{k_g^2\mu }}O({{\beta ^2}}) = {\hat
\xi _b}\left( {\frac{1}{\mu } + 1} \right)O( {{\beta ^2}} ), \end{equation}
which is of second order in bottom slope ![]() $O( {{\beta ^2}} )$ for off-resonant condition (
$O( {{\beta ^2}} )$ for off-resonant condition (![]() $\beta {\mu ^{ - 1}} = O( \beta )$) in intermediated depth, and of first order in bottom slope
$\beta {\mu ^{ - 1}} = O( \beta )$) in intermediated depth, and of first order in bottom slope ![]() $O( \beta )$ for near-resonant condition (
$O( \beta )$ for near-resonant condition (![]() $\beta {\mu ^{ - 1}} = O( 1 )$) in shallow water.
$\beta {\mu ^{ - 1}} = O( 1 )$) in shallow water.
Appendix B. Theoretical calculation of complex amplitude of subharmonic
The amplitude and phase of the complex amplitude of subharmonics ![]() $\hat \xi (x)$ over a plane sloping bottom are shown in figure 6, which is the sum of the group-induced subharmonic
$\hat \xi (x)$ over a plane sloping bottom are shown in figure 6, which is the sum of the group-induced subharmonic ![]() $\hat \xi _g(x)$ and the downwave-propagating free component due to scattering at the toe of the slope
$\hat \xi _g(x)$ and the downwave-propagating free component due to scattering at the toe of the slope ![]() $\hat \xi _{{sc}}$, i.e.
$\hat \xi _{{sc}}$, i.e.
Let ![]() $x=x_0$ denote the coordinate of the toe of the slope. The downwave-propagating component due to toe scattering is calculated as
$x=x_0$ denote the coordinate of the toe of the slope. The downwave-propagating component due to toe scattering is calculated as
 \begin{equation} \hat \xi_{{sc}}(x) = \hat \xi_{{sc}}(x_0) \frac{\hat \xi_h^+(x)}{\hat \xi_h^+(x_0)}, \end{equation}
\begin{equation} \hat \xi_{{sc}}(x) = \hat \xi_{{sc}}(x_0) \frac{\hat \xi_h^+(x)}{\hat \xi_h^+(x_0)}, \end{equation}
where the exact form of ![]() $\hat \xi _h^+(x)$ varies for different theoretical solutions. The boundary value
$\hat \xi _h^+(x)$ varies for different theoretical solutions. The boundary value ![]() $\hat \xi _{{sc}}(x_0)$ is given by equation (29) in Liao et al. (Reference Liao, Li, Liu and Zou2021):
$\hat \xi _{{sc}}(x_0)$ is given by equation (29) in Liao et al. (Reference Liao, Li, Liu and Zou2021):
 $$\begin{align} \hat
\xi_{{sc}}(x_0) &= \frac{\hat \xi_{{LHS62}}\beta}{0.25\beta
- 2\mathrm{i}{k_f}/{k_g}} \times\left\{\left(\frac{k_f^2}{k_g^2}\frac{h}{\left| {\hat
S} \right|}\frac{\mathrm{d}\left| {\hat S}
\right|}{\mathrm{d}h} - 1 - \frac{h}{\mu}\frac{\mathrm{d}\mu}{\mathrm{d}h} \right)\right.\nonumber\\
&\quad \left. + \frac{k_g}{k_f-k_g}\left[\frac{k_f^2}{k_g^2}\left(\frac{2h}{\left|
{\hat S} \right|}\frac{\mathrm{d}\left| {\hat S}
\right|}{\mathrm{d}h} + \frac{h}{k_g}\frac{\mathrm{d}k_g}{\mathrm{d}h} \right) - 1
- \frac{2h}{\mu}\frac{\mathrm{d}\mu}{\mathrm{d}h}\right]\right\}.
\end{align}$$
$$\begin{align} \hat
\xi_{{sc}}(x_0) &= \frac{\hat \xi_{{LHS62}}\beta}{0.25\beta
- 2\mathrm{i}{k_f}/{k_g}} \times\left\{\left(\frac{k_f^2}{k_g^2}\frac{h}{\left| {\hat
S} \right|}\frac{\mathrm{d}\left| {\hat S}
\right|}{\mathrm{d}h} - 1 - \frac{h}{\mu}\frac{\mathrm{d}\mu}{\mathrm{d}h} \right)\right.\nonumber\\
&\quad \left. + \frac{k_g}{k_f-k_g}\left[\frac{k_f^2}{k_g^2}\left(\frac{2h}{\left|
{\hat S} \right|}\frac{\mathrm{d}\left| {\hat S}
\right|}{\mathrm{d}h} + \frac{h}{k_g}\frac{\mathrm{d}k_g}{\mathrm{d}h} \right) - 1
- \frac{2h}{\mu}\frac{\mathrm{d}\mu}{\mathrm{d}h}\right]\right\}.
\end{align}$$ To use the off-resonant solution of Zou (Reference Zou2011), ![]() $\hat \xi _h^+(x)$ is given by (see equations (3.9c)–(3.9d) therein)
$\hat \xi _h^+(x)$ is given by (see equations (3.9c)–(3.9d) therein)
 $$\begin{align} \hat
\xi _h^+ \left( x \right) &= h^{{-}0.25}(x) \nonumber\\
&\quad \times \left\{1 + \frac{h^{{-}0.5}(x)}{2 \mathrm{i} k_f}
\int_{x_0}^{x}h^{{-}0.25}(x')\frac{\mathrm{d}}{\mathrm{d}\,x} \left[h(x') \frac{\mathrm{d}}{\mathrm{d}\,x}
h^{{-}0.25}(x')\right] \mathrm{d}\,x'\right\}
\exp\left({\mathrm{i}\int_{x_0}^{x}k_f \mathrm{d}\,x'}\right).
\end{align}$$
$$\begin{align} \hat
\xi _h^+ \left( x \right) &= h^{{-}0.25}(x) \nonumber\\
&\quad \times \left\{1 + \frac{h^{{-}0.5}(x)}{2 \mathrm{i} k_f}
\int_{x_0}^{x}h^{{-}0.25}(x')\frac{\mathrm{d}}{\mathrm{d}\,x} \left[h(x') \frac{\mathrm{d}}{\mathrm{d}\,x}
h^{{-}0.25}(x')\right] \mathrm{d}\,x'\right\}
\exp\left({\mathrm{i}\int_{x_0}^{x}k_f \mathrm{d}\,x'}\right).
\end{align}$$ Substituting the off-resonant solution of Zou (Reference Zou2011) (4.10) into ![]() $\hat \xi _g(x)$ in (B1) yields
$\hat \xi _g(x)$ in (B1) yields
 $$\begin{align} {\hat
\xi (x)} &={-} \frac{{\hat S}}{{\rho gh\mu }}\left\{ {1 +
\frac{{\mathrm{i}\beta }}{\mu }\left[ {\left(
{\frac{{2h}}{{\left| {\hat S}
\right|}}\frac{{\mathrm{d}\left| {\hat S}
\right|}}{{\mathrm{d}h}} +
\frac{h}{{{k_g}}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}h}}}
\right)\left( {1 - \mu } \right) - 1 - \frac{{2h}}{\mu
}\frac{{\mathrm{d}\mu }}{{\mathrm{d}h}}} \right]} \right\} \nonumber\\
&\quad + \hat \xi_{{sc}}(x_0) \frac{\hat
\xi_h^+(x)}{\hat \xi_h^+(x_0)}.
\end{align}$$
$$\begin{align} {\hat
\xi (x)} &={-} \frac{{\hat S}}{{\rho gh\mu }}\left\{ {1 +
\frac{{\mathrm{i}\beta }}{\mu }\left[ {\left(
{\frac{{2h}}{{\left| {\hat S}
\right|}}\frac{{\mathrm{d}\left| {\hat S}
\right|}}{{\mathrm{d}h}} +
\frac{h}{{{k_g}}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}h}}}
\right)\left( {1 - \mu } \right) - 1 - \frac{{2h}}{\mu
}\frac{{\mathrm{d}\mu }}{{\mathrm{d}h}}} \right]} \right\} \nonumber\\
&\quad + \hat \xi_{{sc}}(x_0) \frac{\hat
\xi_h^+(x)}{\hat \xi_h^+(x_0)}.
\end{align}$$ To use the near-resonant solution of Liao et al. (Reference Liao, Li, Liu and Zou2021), ![]() $\hat \xi _h^+(x)$ is given by (see equation (13) therein)
$\hat \xi _h^+(x)$ is given by (see equation (13) therein)
 \begin{equation} \hat \xi _h^+ \left( x
\right) = [k_g(x)h(x)]^{{-}0.5}
\exp\Biggl({\mathrm{i}\int_{x_0}^x\Biggl(1-\frac{\mu}{2}\Biggr)k_g\,\mathrm{d}\,x'}\Biggr).
\end{equation}
\begin{equation} \hat \xi _h^+ \left( x
\right) = [k_g(x)h(x)]^{{-}0.5}
\exp\Biggl({\mathrm{i}\int_{x_0}^x\Biggl(1-\frac{\mu}{2}\Biggr)k_g\,\mathrm{d}\,x'}\Biggr).
\end{equation}
Substituting (4.12) and (B2)–(B6) into (B1) yields
 \begin{equation} \hat \xi(x) = \frac{\hat \xi_h^+(x)}{\hat \xi_h^+(x_0)}\left[\hat \xi_{{sc}}(x_0) + \hat \xi_b(x_0) + \int_{x_0}^x {\frac{{{{\hat f}_{{M}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_g}\left(\kern0.7pt y \right)}}\frac{\hat \xi_h^+(x_0)}{\hat \xi_h^+(\kern0.7pt y )}\,\mathrm{d} y}\right], \end{equation}
\begin{equation} \hat \xi(x) = \frac{\hat \xi_h^+(x)}{\hat \xi_h^+(x_0)}\left[\hat \xi_{{sc}}(x_0) + \hat \xi_b(x_0) + \int_{x_0}^x {\frac{{{{\hat f}_{{M}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_g}\left(\kern0.7pt y \right)}}\frac{\hat \xi_h^+(x_0)}{\hat \xi_h^+(\kern0.7pt y )}\,\mathrm{d} y}\right], \end{equation}
where ![]() $\hat \xi _b(x_0)$ is given by (4.10).
$\hat \xi _b(x_0)$ is given by (4.10).
Comparison of (4.16) and (4.12) indicates that, to use the near-resonant solution of Janssen et al. (Reference Janssen, Battjes and van Dongeren2003), we simply replace ![]() ${\hat f}_{{M}}$ in the above equation with
${\hat f}_{{M}}$ in the above equation with ![]() ${\hat f}_{{M}} + {\hat f}_{{S}}$, i.e.
${\hat f}_{{M}} + {\hat f}_{{S}}$, i.e.
 \begin{equation} \hat \xi(x) = \frac{\hat \xi_h^+(x)}{\hat \xi_h^+(x_0)}\left[\hat \xi_{{sc}}(x_0) + \hat \xi_b(x_0) + \int_{x_0}^x {\frac{{{{\hat f}_{{M}}}\left(\kern0.7pt y \right) + {{\hat f}_{{S}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_g}\left(\kern0.7pt y \right)}}\frac{\hat \xi_h^+(x_0)}{\hat \xi_h^+(\kern0.7pt y )}\,\mathrm{d} y}\right]. \end{equation}
\begin{equation} \hat \xi(x) = \frac{\hat \xi_h^+(x)}{\hat \xi_h^+(x_0)}\left[\hat \xi_{{sc}}(x_0) + \hat \xi_b(x_0) + \int_{x_0}^x {\frac{{{{\hat f}_{{M}}}\left(\kern0.7pt y \right) + {{\hat f}_{{S}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_g}\left(\kern0.7pt y \right)}}\frac{\hat \xi_h^+(x_0)}{\hat \xi_h^+(\kern0.7pt y )}\,\mathrm{d} y}\right]. \end{equation} To use the present solution, ![]() $\hat \xi _h^+(x)$ is replaced by (3.35), i.e.
$\hat \xi _h^+(x)$ is replaced by (3.35), i.e.
The present solution (3.16) is calculated by replacing ![]() $a$ with
$a$ with ![]() $x_0$, with
$x_0$, with ![]() $\hat \xi _h^\pm$ given by (3.35) and
$\hat \xi _h^\pm$ given by (3.35) and ![]() $\hat \xi _f^\pm (x_0)$ given by
$\hat \xi _f^\pm (x_0)$ given by ![]() $\hat \xi _b^\pm (x_0)$ in (4.8). According to the analysis in § 4.3.1, the present solution (3.39) is accurate to leading order for the near-resonance condition. Hence according to (3.32) and (3.36), the source field (3.7) to leading order is
$\hat \xi _b^\pm (x_0)$ in (4.8). According to the analysis in § 4.3.1, the present solution (3.39) is accurate to leading order for the near-resonance condition. Hence according to (3.32) and (3.36), the source field (3.7) to leading order is
Therefore, the expression of solution (3.16) for the calculation in figure 6 is given by
 \begin{align} \hat \xi(x) = \hat \xi_{{sc}}(x) + \hat \xi_b^+(x_0)\frac{\hat \xi_h^+(x)}{\hat \xi_h^+(x_0)} + \hat \xi_b^-(x_0)\frac{\hat \xi_h^-(x)}{\hat \xi_h^-(x_0)} + \int_{x_0}^x\frac{\hat f_{M}(\kern0.7pt y )}{2\mathrm{i}k_f(\kern0.7pt y )}\left[\frac{\hat \xi_h^+(x)}{\hat \xi_h^+(\kern0.7pt y )} - \frac{\hat \xi_h^-(x)}{\hat \xi_h^-(\kern0.7pt y )}\right]\,\mathrm{d} y, \end{align}
\begin{align} \hat \xi(x) = \hat \xi_{{sc}}(x) + \hat \xi_b^+(x_0)\frac{\hat \xi_h^+(x)}{\hat \xi_h^+(x_0)} + \hat \xi_b^-(x_0)\frac{\hat \xi_h^-(x)}{\hat \xi_h^-(x_0)} + \int_{x_0}^x\frac{\hat f_{M}(\kern0.7pt y )}{2\mathrm{i}k_f(\kern0.7pt y )}\left[\frac{\hat \xi_h^+(x)}{\hat \xi_h^+(\kern0.7pt y )} - \frac{\hat \xi_h^-(x)}{\hat \xi_h^-(\kern0.7pt y )}\right]\,\mathrm{d} y, \end{align}where
with ![]() $\hat \xi _g^+ ( x )$ and
$\hat \xi _g^+ ( x )$ and ![]() $\hat \xi _g^- ( x )$ being
$\hat \xi _g^- ( x )$ being
 \begin{equation} \left. \begin{aligned} \hat \xi _g^+ \left( x \right) & = \hat \xi_b^+(x_0)\frac{\hat \xi_h^+(x)}{\hat \xi_h^+(x_0)} + \int_{x_0}^x {\frac{{{{\hat f}_{{M}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_f}\left(\kern0.7pt y \right)}} \frac{\hat \xi_h^+(x)}{\hat \xi_h^+(\kern0.7pt y )}\,\mathrm{d} y},\\ \hat \xi _g^- \left( x \right) & = \hat \xi_b^-(x_0)\frac{\hat \xi_h^-(x)}{\hat \xi_h^-(x_0)} - \int_{x_0}^x {\frac{{{{\hat f}_{{M}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_f}\left(\kern0.7pt y \right)}}\frac{\hat \xi_h^-(x)}{\hat \xi_h^-(\kern0.7pt y )}\mathrm{d} y}. \end{aligned} \right\} \end{equation}
\begin{equation} \left. \begin{aligned} \hat \xi _g^+ \left( x \right) & = \hat \xi_b^+(x_0)\frac{\hat \xi_h^+(x)}{\hat \xi_h^+(x_0)} + \int_{x_0}^x {\frac{{{{\hat f}_{{M}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_f}\left(\kern0.7pt y \right)}} \frac{\hat \xi_h^+(x)}{\hat \xi_h^+(\kern0.7pt y )}\,\mathrm{d} y},\\ \hat \xi _g^- \left( x \right) & = \hat \xi_b^-(x_0)\frac{\hat \xi_h^-(x)}{\hat \xi_h^-(x_0)} - \int_{x_0}^x {\frac{{{{\hat f}_{{M}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_f}\left(\kern0.7pt y \right)}}\frac{\hat \xi_h^-(x)}{\hat \xi_h^-(\kern0.7pt y )}\mathrm{d} y}. \end{aligned} \right\} \end{equation}
Combined with the moving-breakpoint forcing model, the present solution is applied to test A-4 in the experiment of Van Noorloos (Reference Van Noorloos2003). Region B ![]() $[x_a, x_c]$ is first identified as shown in figure 11. Then, according to (5.5), the amplitudes of bichromatic waves,
$[x_a, x_c]$ is first identified as shown in figure 11. Then, according to (5.5), the amplitudes of bichromatic waves, ![]() $A_1(x_a)$ and
$A_1(x_a)$ and ![]() $A_1(x_c)$, are estimated as
$A_1(x_c)$, are estimated as ![]() $\gamma h / [2\sqrt {2}(1 - \delta )]$ and
$\gamma h / [2\sqrt {2}(1 - \delta )]$ and ![]() $\gamma h / [2\sqrt {2}(1 + \delta )]$ assuming
$\gamma h / [2\sqrt {2}(1 + \delta )]$ assuming ![]() $A_1(x)$ varies linearly from
$A_1(x)$ varies linearly from ![]() $A_1(x_0)=0.06$ m to
$A_1(x_0)=0.06$ m to ![]() $A_1(x_a)$ and
$A_1(x_a)$ and ![]() $A_1(x_c)$. For test B-5, the wave parameters are
$A_1(x_c)$. For test B-5, the wave parameters are ![]() $[f_1, f_2] = [0.6470, 0.5005]$ Hz,
$[f_1, f_2] = [0.6470, 0.5005]$ Hz, ![]() $[A_1, A_2] = [0.06, 0.036]$ m,
$[A_1, A_2] = [0.06, 0.036]$ m, ![]() $[x_a, x_c] = [5, 10.5]$ m,
$[x_a, x_c] = [5, 10.5]$ m, ![]() $\delta = 0.6$ and
$\delta = 0.6$ and ![]() $\gamma = 0.68$. Then
$\gamma = 0.68$. Then ![]() $\hat \xi _g^+(x)$ and
$\hat \xi _g^+(x)$ and ![]() $\hat \xi _g^-(x)$ in region B are calculated using (B13) but now the forcing term
$\hat \xi _g^-(x)$ in region B are calculated using (B13) but now the forcing term ![]() $\hat {f}_{{M}}$ in
$\hat {f}_{{M}}$ in ![]() $[x_a, x_c]$ is determined using (5.7) as
$[x_a, x_c]$ is determined using (5.7) as
Note that ![]() $\hat \xi _g^-(x)$ in the region shoreward of
$\hat \xi _g^-(x)$ in the region shoreward of ![]() $x_a$ is set to zero because the present model assumes zero groupiness and hence zero group forcing in this region; therefore theoretically no upwave-propagating component of group-induced subharmonic exists.
$x_a$ is set to zero because the present model assumes zero groupiness and hence zero group forcing in this region; therefore theoretically no upwave-propagating component of group-induced subharmonic exists.

Figure 11. Left axis: the root-mean-square (RMS) wave height of primary waves of test A-4 in the experiment of Van Noorloos (Reference Van Noorloos2003); right axis: bottom elevation of the physical model. Parameters ![]() $f_i$ and
$f_i$ and ![]() $A_i$ (
$A_i$ (![]() $i=1,2$) are the frequency and amplitude of the two components of bichromatic waves tested. Rate
$i=1,2$) are the frequency and amplitude of the two components of bichromatic waves tested. Rate ![]() $\delta =A_2/A_1$ is the modulation rate and
$\delta =A_2/A_1$ is the modulation rate and ![]() $\gamma =\textrm {significant breaking height/depth}$ is the breaker index. The seaward boundary of moving-breakpoint region
$\gamma =\textrm {significant breaking height/depth}$ is the breaker index. The seaward boundary of moving-breakpoint region ![]() $x_c$ is where primary wave height starts to decay, and the shoreward boundary location
$x_c$ is where primary wave height starts to decay, and the shoreward boundary location ![]() $x_a$ is 26.7 m from wave paddles where the smallest waves break (cf. § 5.1.1 in Van Noorloos Reference Van Noorloos2003).
$x_a$ is 26.7 m from wave paddles where the smallest waves break (cf. § 5.1.1 in Van Noorloos Reference Van Noorloos2003).
Appendix C. Generation and formation of group-induced subharmonic
Unlike previous studies, the present unified solution of group-induced subharmonic for all water depths is constructed based on Green's function. Accordingly, the group-forcing field is divided into successive pulses distributed in space, and the group-induced subharmonic is the superposition of all the free subharmonics generated by each pulse in both directions. As a result, the group-induced subharmonic is modulated by and bound to the group-forcing field and, therefore, the wave group. To understand the evolution of the subharmonic from intermediate to shallow water, the emission, propagation and interference of the free subharmonics induced by group forcing are examined in this appendix.
C.1. Emission of free subharmonics due to group forcing
The nonlinear short-wave group forcing of the subharmonic is represented by the radiation stress gradients ![]() $\partial ^{2} \tilde {S} / \partial x^{2}$ in the governing equation (2.14). For stationary bichromatic waves, at any given position,
$\partial ^{2} \tilde {S} / \partial x^{2}$ in the governing equation (2.14). For stationary bichromatic waves, at any given position, ![]() $\partial ^{2} \tilde {S} / \partial x^{2}$ oscillates with the period of the wave group, and so does the induced free subharmonic. The emission of the free subharmonic is described by its initial complex amplitude generated per unit distance, which constitutes the source field of group-induced subharmonic,
$\partial ^{2} \tilde {S} / \partial x^{2}$ oscillates with the period of the wave group, and so does the induced free subharmonic. The emission of the free subharmonic is described by its initial complex amplitude generated per unit distance, which constitutes the source field of group-induced subharmonic, ![]() $\hat \sigma$. For linear problems, the source field of the group-induced subharmonic is given by
$\hat \sigma$. For linear problems, the source field of the group-induced subharmonic is given by ![]() $\hat \sigma (\kern0.7pt y ) = \hat f(\kern0.7pt y )G(\kern0.7pt {y,y} )$, where
$\hat \sigma (\kern0.7pt y ) = \hat f(\kern0.7pt y )G(\kern0.7pt {y,y} )$, where ![]() $G(\kern0.7pt {y,y} )$ (3.10) is the local response of surface elevation to periodic forcing with unit complex amplitude and
$G(\kern0.7pt {y,y} )$ (3.10) is the local response of surface elevation to periodic forcing with unit complex amplitude and ![]() $\hat f(\kern0.7pt y )$ (3.2) is the external group-forcing field with complex amplitude. Since
$\hat f(\kern0.7pt y )$ (3.2) is the external group-forcing field with complex amplitude. Since ![]() $\hat f$ is modulated by wave groups, so are the initial amplitude and phase of the emitted free subharmonics.
$\hat f$ is modulated by wave groups, so are the initial amplitude and phase of the emitted free subharmonics.
For wave groups over continuous 1-D topography with mild sloping bottom, at leading order of bottom slope, the group forcing ![]() $\hat f$ is in phase with radiation stress (
$\hat f$ is in phase with radiation stress ( ![]() ${\hat f_{{M}}}$ in (3.34)) and the local response of surface elevation is
${\hat f_{{M}}}$ in (3.34)) and the local response of surface elevation is ![]() $G(\kern0.7pt y, y)=1 /(2 \mathrm {i} k_{f})$ (3.36), indicating that the source field is
$G(\kern0.7pt y, y)=1 /(2 \mathrm {i} k_{f})$ (3.36), indicating that the source field is ![]() ${\rm \pi} /2$ ahead of the wave groups. This phase relationship is physically understandable since, as indicated by the momentum equation (2.13), the force directly exerted onto the water body is the radiation stress gradient, which is
${\rm \pi} /2$ ahead of the wave groups. This phase relationship is physically understandable since, as indicated by the momentum equation (2.13), the force directly exerted onto the water body is the radiation stress gradient, which is ![]() ${\rm \pi} /2$ ahead of wave groups. At leading order, the magnitude of the source field is proportional to
${\rm \pi} /2$ ahead of wave groups. At leading order, the magnitude of the source field is proportional to ![]() $| {\hat \sigma } | \propto k_g^2| {\hat S} |{h^{ - 0.5}}$ (3.38), which increases with decreasing depth as
$| {\hat \sigma } | \propto k_g^2| {\hat S} |{h^{ - 0.5}}$ (3.38), which increases with decreasing depth as ![]() $| {\hat \sigma } | \propto {h^{ - 2}}$ for a conservative shoaling process in shallow water.
$| {\hat \sigma } | \propto {h^{ - 2}}$ for a conservative shoaling process in shallow water.
C.2. Propagation of emitted subharmonics
For wave groups over continuous 1-D topography, under periodic group forcing, two subharmonics radiate away from the source location freely. Over a mild sloping bottom, neglecting reflection and dissipation, the amplitude transformation of the free subharmonic from its source point ![]() $y$ to an observation point
$y$ to an observation point ![]() $x$ is described by Green's law, i.e.
$x$ is described by Green's law, i.e. ![]() ${\textrm {amplitude}} \propto {h^{ - 0.25}}$. Considering the phase change from
${\textrm {amplitude}} \propto {h^{ - 0.25}}$. Considering the phase change from ![]() $y$ to
$y$ to ![]() $x$, the transfer function of complex amplitude of the free subharmonic,
$x$, the transfer function of complex amplitude of the free subharmonic, ![]() $\hat \sigma (\kern0.7pt y )\,\mathrm {d} y$, is given by
$\hat \sigma (\kern0.7pt y )\,\mathrm {d} y$, is given by ![]() $[h(x) / h(\kern0.7pt y )]^{-0.25} \exp ({\mathrm {i} |\int _{y}^{x} k_{f} \,\mathrm {d}\,x^{\prime } |})$. As shown in § 4, this simple transfer function reduces the present solution to existing solutions for both off-resonance condition (
$[h(x) / h(\kern0.7pt y )]^{-0.25} \exp ({\mathrm {i} |\int _{y}^{x} k_{f} \,\mathrm {d}\,x^{\prime } |})$. As shown in § 4, this simple transfer function reduces the present solution to existing solutions for both off-resonance condition (![]() $\beta {\mu ^{ - 1}} = O( \beta )$) in intermediate depth and near-resonance condition (
$\beta {\mu ^{ - 1}} = O( \beta )$) in intermediate depth and near-resonance condition (![]() $\beta {\mu ^{ - 1}} = O( 1 )$) in shallow water.
$\beta {\mu ^{ - 1}} = O( 1 )$) in shallow water.
C.3. Interference of subharmonics
The linear superposition of all the emitted free subharmonics from each source location ![]() $y$ yields the group-induced subharmonic at an observation point
$y$ yields the group-induced subharmonic at an observation point ![]() $x$, with complex amplitude
$x$, with complex amplitude ![]() $\hat \xi _g( x )$. Taking the wave group direction as the downwave direction,
$\hat \xi _g( x )$. Taking the wave group direction as the downwave direction, ![]() ${\hat \xi _g} = \hat \xi _g^+ + \hat \xi _g^-$, where
${\hat \xi _g} = \hat \xi _g^+ + \hat \xi _g^-$, where ![]() $\hat \xi _g^+$ and
$\hat \xi _g^+$ and ![]() $\hat \xi _g^-$ are the complex amplitudes of downwave- and upwave-propagating components, respectively. At leading order, the phase of the integrand in the solution for
$\hat \xi _g^-$ are the complex amplitudes of downwave- and upwave-propagating components, respectively. At leading order, the phase of the integrand in the solution for ![]() $\hat \xi ^{\pm }_g$ (3.39) varies with
$\hat \xi ^{\pm }_g$ (3.39) varies with ![]() $y$ as
$y$ as ![]() $\int ^{y}(k_g \pm k_f)\, \mathrm {d}\,x'$. This means that, at any observation point
$\int ^{y}(k_g \pm k_f)\, \mathrm {d}\,x'$. This means that, at any observation point ![]() $x$, the phase of each downwave-propagating subharmonic varies slowly with its source location
$x$, the phase of each downwave-propagating subharmonic varies slowly with its source location ![]() $y$ as
$y$ as ![]() $\int ^y {({k_g} - {k_f})\,\mathrm {d}\,x'}$, while that of the upwave-propagating subharmonic varies much faster as
$\int ^y {({k_g} - {k_f})\,\mathrm {d}\,x'}$, while that of the upwave-propagating subharmonic varies much faster as ![]() $\int ^y {({k_g} + {k_f})\,\mathrm {d}\,x'}$. The phase dependence of collocated free subharmonics on their source locations determines the maximum length of the source region from which the emitted subharmonics have phases close to each other so that they interfere with each other constructively. The longer this region is, the larger the superposed subharmonic amplitude becomes. The maximum lengths of source region are of order
$\int ^y {({k_g} + {k_f})\,\mathrm {d}\,x'}$. The phase dependence of collocated free subharmonics on their source locations determines the maximum length of the source region from which the emitted subharmonics have phases close to each other so that they interfere with each other constructively. The longer this region is, the larger the superposed subharmonic amplitude becomes. The maximum lengths of source region are of order ![]() ${\rm \pi} /(k_{g}-k_{f})$ and
${\rm \pi} /(k_{g}-k_{f})$ and ![]() ${\rm \pi} /(k_{g}+k_{f})$ for the downwave- and upwave-propagating subharmonics, respectively. Consequently, the superposed amplitude of the downwave-propagating subharmonic
${\rm \pi} /(k_{g}+k_{f})$ for the downwave- and upwave-propagating subharmonics, respectively. Consequently, the superposed amplitude of the downwave-propagating subharmonic ![]() $| {\hat \xi _g^+ } |$ is about
$| {\hat \xi _g^+ } |$ is about ![]() $(k_g+k_f)/(k_g-k_f)$ times
$(k_g+k_f)/(k_g-k_f)$ times ![]() $| {\hat \xi _g^- } |$, assuming that the source field is of the same order of magnitude in the entire domain. This underlying mechanism explains the stronger resonance of downwave-propagating subharmonics than upwave-propagating subharmonics.
$| {\hat \xi _g^- } |$, assuming that the source field is of the same order of magnitude in the entire domain. This underlying mechanism explains the stronger resonance of downwave-propagating subharmonics than upwave-propagating subharmonics.
In shallow water, near resonance occurs, i.e. ![]() $k_g \approx k_f$, and the downwave-propagating free subharmonics travel at the same speed as the source field; hence the initial phase difference of
$k_g \approx k_f$, and the downwave-propagating free subharmonics travel at the same speed as the source field; hence the initial phase difference of ![]() ${\rm \pi} /2$ between each emitted downwave-propagating component and wave groups remains the same during propagation and so does the superposed downwave-propagating subharmonic. Moreover, all downwave-propagating subharmonics are in phase with each other and they interfere with each other constructively (figure 5). Consequently, as elucidated by (3.42), the superposed amplitude of downwave-propagating free subharmonics increases linearly with the travel distance of wave groups. In practice, however, the rate of increase with travel distance is reduced by the dissipating group forcing due to bottom friction, nonlinear energy transfer to subharmonics or depth-induced wave breaking.
${\rm \pi} /2$ between each emitted downwave-propagating component and wave groups remains the same during propagation and so does the superposed downwave-propagating subharmonic. Moreover, all downwave-propagating subharmonics are in phase with each other and they interfere with each other constructively (figure 5). Consequently, as elucidated by (3.42), the superposed amplitude of downwave-propagating free subharmonics increases linearly with the travel distance of wave groups. In practice, however, the rate of increase with travel distance is reduced by the dissipating group forcing due to bottom friction, nonlinear energy transfer to subharmonics or depth-induced wave breaking.
Appendix D. Influence of entire topography on group-induced subharmonic
The group-induced subharmonic at any observation position includes components generated in regions on the upwave and downwave sides, meaning that the group-induced subharmonic is dependent on the whole profile of the topography. To elucidate how the local group-induced subharmonic is influenced by the topography, a conceptual model is proposed and analysed below.
Consider a fixed wave train travelling across topographies, ![]() $h_{I}(x )$ and
$h_{I}(x )$ and ![]() $h_{II}(x)$, with
$h_{II}(x)$, with ![]() $h_{I}(a) = h_{II}( a )$ at the boundary
$h_{I}(a) = h_{II}( a )$ at the boundary ![]() $x=a$ (figure 12a). The topography is assumed to be smooth enough so that the scattering effect due to discontinuity in bottom slope or bottom curvature is negligible (Zou Reference Zou2011). Let
$x=a$ (figure 12a). The topography is assumed to be smooth enough so that the scattering effect due to discontinuity in bottom slope or bottom curvature is negligible (Zou Reference Zou2011). Let ![]() $h_{I}(x)$ and
$h_{I}(x)$ and ![]() $h_{II}(x)$ be different in
$h_{II}(x)$ be different in ![]() $a < x < b$ only, i.e.
$a < x < b$ only, i.e.
 \begin{equation}
\left. \begin{aligned} & \left[\begin{array}{@{}c@{}} h_{{I}}(x) \\
\dfrac{\mathrm{d}}{\mathrm{d}\,x} h_{{I}}(x) \\
\dfrac{\mathrm{d}^{2}}{\mathrm{d}\,x^{2}} h_{{I}}(x)
\end{array}\right] \not\equiv\left[\begin{array}{@{}c@{}}
h_{{II}}(x) \\
\dfrac{\mathrm{d}}{\mathrm{d}\,x} h_{{II}}(x) \\
\dfrac{\mathrm{d}^{2}}{\mathrm{d}\,x^{2}} h_{{II}}(x)
\end{array}\right], \quad \text{ for } a< x< b,\\
& \left[\begin{array}{@{}c@{}} h_{{I}}(x) \\
\dfrac{\mathrm{d}}{\mathrm{d}\,x} h_{{I}}(x) \\
\dfrac{\mathrm{d}^{2}}{\mathrm{d}\,x^{2}} h_{{I}}(x)
\end{array}\right] \equiv\left[\begin{array}{@{}c@{}} h_{{II}}(x) \\
\dfrac{\mathrm{d}}{\mathrm{d}\,x} h_{{II}}(x) \\
\dfrac{\mathrm{d}^{2}}{\mathrm{d}\,x^{2}} h_{{II}}(x)
\end{array}\right],\quad \text{for } x \geq b.
\end{aligned} \right\}
\end{equation}
\begin{equation}
\left. \begin{aligned} & \left[\begin{array}{@{}c@{}} h_{{I}}(x) \\
\dfrac{\mathrm{d}}{\mathrm{d}\,x} h_{{I}}(x) \\
\dfrac{\mathrm{d}^{2}}{\mathrm{d}\,x^{2}} h_{{I}}(x)
\end{array}\right] \not\equiv\left[\begin{array}{@{}c@{}}
h_{{II}}(x) \\
\dfrac{\mathrm{d}}{\mathrm{d}\,x} h_{{II}}(x) \\
\dfrac{\mathrm{d}^{2}}{\mathrm{d}\,x^{2}} h_{{II}}(x)
\end{array}\right], \quad \text{ for } a< x< b,\\
& \left[\begin{array}{@{}c@{}} h_{{I}}(x) \\
\dfrac{\mathrm{d}}{\mathrm{d}\,x} h_{{I}}(x) \\
\dfrac{\mathrm{d}^{2}}{\mathrm{d}\,x^{2}} h_{{I}}(x)
\end{array}\right] \equiv\left[\begin{array}{@{}c@{}} h_{{II}}(x) \\
\dfrac{\mathrm{d}}{\mathrm{d}\,x} h_{{II}}(x) \\
\dfrac{\mathrm{d}^{2}}{\mathrm{d}\,x^{2}} h_{{II}}(x)
\end{array}\right],\quad \text{for } x \geq b.
\end{aligned} \right\}
\end{equation}
Figure 12. A conceptual model of a fixed wave train propagating from ![]() $a$ to
$a$ to ![]() $x$ over two different topographies. (a) Topographies
$x$ over two different topographies. (a) Topographies ![]() ${h_{{I}}}( x )$ and
${h_{{I}}}( x )$ and ![]() ${h_{{{II}}}}( x )$, which are different in
${h_{{{II}}}}( x )$, which are different in ![]() $a < x < b$ only. (b) Spatial evolution of the amplitude of downwave-propagating group-induced subharmonic
$a < x < b$ only. (b) Spatial evolution of the amplitude of downwave-propagating group-induced subharmonic ![]() $| {\hat \xi _{g,i}^+ ( x )} |,\ i = {\textrm {I, II}}$ (solid lines). Here
$| {\hat \xi _{g,i}^+ ( x )} |,\ i = {\textrm {I, II}}$ (solid lines). Here ![]() $\hat \xi _{g,i}^+ ( x )$ in
$\hat \xi _{g,i}^+ ( x )$ in ![]() $x \geqslant b$ includes two components: one is generated in
$x \geqslant b$ includes two components: one is generated in ![]() $x \geqslant b$ (dotted line), which is the same for
$x \geqslant b$ (dotted line), which is the same for ![]() ${h_{{I}}}( x )$ and
${h_{{I}}}( x )$ and ![]() ${h_{{{II}}}}( x )$, and the other is generated in
${h_{{{II}}}}( x )$, and the other is generated in ![]() $a < x < b$ (dashed lines).
$a < x < b$ (dashed lines).
The downwave-propagating group-induced subharmonic ![]() $\hat \xi _g^+ ( x )$ can be derived from (3.12a):
$\hat \xi _g^+ ( x )$ can be derived from (3.12a):
 \begin{equation} \hat \xi _{g,i}^+ \left( x \right) = \int_a^x {{{\hat \sigma }_i}\left(\kern0.7pt y \right)\frac{{\hat \xi _{h,i}^+ \left( x \right)}}{{\hat \xi _{h,i}^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y} ,\quad i = {\text{I}},{\text{II}}, \end{equation}
\begin{equation} \hat \xi _{g,i}^+ \left( x \right) = \int_a^x {{{\hat \sigma }_i}\left(\kern0.7pt y \right)\frac{{\hat \xi _{h,i}^+ \left( x \right)}}{{\hat \xi _{h,i}^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y} ,\quad i = {\text{I}},{\text{II}}, \end{equation}
which, in ![]() $x \geqslant b$, can be decomposed into
$x \geqslant b$, can be decomposed into
 \begin{equation} \hat \xi _{g,i}^+ \left( x \right) = \hat \xi _{g,i}^+ \left( b \right)\frac{{\hat \xi _{h,i}^+ \left( x \right)}}{{\hat \xi _{h,i}^+ \left( b \right)}} + \int_b^x {{{\hat \sigma }_i}\left(\kern0.7pt y \right)\frac{{\hat \xi _{h,i}^+ \left( x \right)}}{{\hat \xi _{h,i}^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y} ,\quad i = {\text{I}},{\text{II}}. \end{equation}
\begin{equation} \hat \xi _{g,i}^+ \left( x \right) = \hat \xi _{g,i}^+ \left( b \right)\frac{{\hat \xi _{h,i}^+ \left( x \right)}}{{\hat \xi _{h,i}^+ \left( b \right)}} + \int_b^x {{{\hat \sigma }_i}\left(\kern0.7pt y \right)\frac{{\hat \xi _{h,i}^+ \left( x \right)}}{{\hat \xi _{h,i}^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y} ,\quad i = {\text{I}},{\text{II}}. \end{equation}
Equation (D3) shows that ![]() $\hat \xi _g^+ ( x )$ in
$\hat \xi _g^+ ( x )$ in ![]() $x \geqslant b$ includes two components: the first term on the right-hand side corresponds to a free mode component generated in
$x \geqslant b$ includes two components: the first term on the right-hand side corresponds to a free mode component generated in ![]() $a < x < b$; the second term is the component generated in the region between
$a < x < b$; the second term is the component generated in the region between ![]() $b$ and
$b$ and ![]() $x$. The influence of topography in
$x$. The influence of topography in ![]() $a < x < b$ on the group-induced subharmonic in
$a < x < b$ on the group-induced subharmonic in ![]() $x \geq b$ is therefore twofold.
$x \geq b$ is therefore twofold.
Firstly, topographies ![]() $h_{I}( x )$ and
$h_{I}( x )$ and ![]() $h_{II}( x )$ in
$h_{II}( x )$ in ![]() $a < x < b$ will lead to different emission and propagation processes of downwave-propagating free subharmonics induced by group forcing. Consequently, the interference pattern of these subharmonics at
$a < x < b$ will lead to different emission and propagation processes of downwave-propagating free subharmonics induced by group forcing. Consequently, the interference pattern of these subharmonics at ![]() $b$ is different, resulting in different subharmonics entering
$b$ is different, resulting in different subharmonics entering ![]() $x \geq b$, as shown in figure 12(b) by the different boundary values of
$x \geq b$, as shown in figure 12(b) by the different boundary values of ![]() $\hat \xi _{{{g,I}}}^+ ( b )$ and
$\hat \xi _{{{g,I}}}^+ ( b )$ and ![]() $\hat \xi _{{{g,II}}}^+ ( b )$ for
$\hat \xi _{{{g,II}}}^+ ( b )$ for ![]() $\hat \xi _{g,{{I}}}^+ ( x )$ and
$\hat \xi _{g,{{I}}}^+ ( x )$ and ![]() $\hat \xi _{g,{{II}}}^+ ( x )$ in
$\hat \xi _{g,{{II}}}^+ ( x )$ in ![]() $x \geq b$, respectively. Similarly, changing the topography on the downwave side of
$x \geq b$, respectively. Similarly, changing the topography on the downwave side of ![]() $x$ can also alter the upwave-propagating component.
$x$ can also alter the upwave-propagating component.
Secondly, the second term on the right-hand side of (D3) is also affected by the topography in ![]() $a < x < b$. On the one hand, the condition (D1) ensures that in
$a < x < b$. On the one hand, the condition (D1) ensures that in ![]() $x \geq b$ the homogeneous solution
$x \geq b$ the homogeneous solution ![]() $\hat \xi _{h,{{I}}}^+$ can only differ from
$\hat \xi _{h,{{I}}}^+$ can only differ from ![]() $\hat \xi _{h,{{II}}}^+$ by a constant coefficient, which has no effect on
$\hat \xi _{h,{{II}}}^+$ by a constant coefficient, which has no effect on ![]() $G(\kern0.7pt y,y)$ according to (3.10). On the other hand, according to (3.32), the forcing field can be expressed as
$G(\kern0.7pt y,y)$ according to (3.10). On the other hand, according to (3.32), the forcing field can be expressed as
 $$\begin{align} {\hat
f_i}\left( x \right) &= \frac{{\hat S\left( a
\right)}}{{\rho g}}\left[
{\frac{{k_{g,i}^2}}{{{h_i}}}{{\left( { -
\frac{1}{{k_g^2\left| {\hat S}
\right|}}\frac{{{\mathrm{d}^2}\left| {\hat S}
\right|}}{{\mathrm{d}\,{x^2}}} -
\frac{{\mathrm{2i}}}{{{k_g}\left| {\hat S}
\right|}}\frac{{\mathrm{d}\left| {\hat S}
\right|}}{{\mathrm{d}\,x}} -
\frac{\mathrm{i}}{{k_g^2}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}\,x}} + 1} \right)}_i}\left| {\frac{{{{\hat S}_i}\left( x
\right)}}{{\hat S\left( a \right)}}} \right|} \right]\nonumber\\
&\quad \times{\exp\left({\mathrm{i}\int_a^x
{{k_{g,i}}\,\mathrm{d} y} }\right)},\quad i =
{\text{I}},{\text{II}}.
\end{align}$$
$$\begin{align} {\hat
f_i}\left( x \right) &= \frac{{\hat S\left( a
\right)}}{{\rho g}}\left[
{\frac{{k_{g,i}^2}}{{{h_i}}}{{\left( { -
\frac{1}{{k_g^2\left| {\hat S}
\right|}}\frac{{{\mathrm{d}^2}\left| {\hat S}
\right|}}{{\mathrm{d}\,{x^2}}} -
\frac{{\mathrm{2i}}}{{{k_g}\left| {\hat S}
\right|}}\frac{{\mathrm{d}\left| {\hat S}
\right|}}{{\mathrm{d}\,x}} -
\frac{\mathrm{i}}{{k_g^2}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}\,x}} + 1} \right)}_i}\left| {\frac{{{{\hat S}_i}\left( x
\right)}}{{\hat S\left( a \right)}}} \right|} \right]\nonumber\\
&\quad \times{\exp\left({\mathrm{i}\int_a^x
{{k_{g,i}}\,\mathrm{d} y} }\right)},\quad i =
{\text{I}},{\text{II}}.
\end{align}$$ Assuming conservation of energy flux of the primary wave, according to (2.11), ![]() $| {\hat S} |$ is only a function of water depth; hence, by (D4),
$| {\hat S} |$ is only a function of water depth; hence, by (D4), ![]() ${\hat f_i}$ excluding the phase factor of wave groups is a function of water depth, bottom slope and bottom curvature, which are the same for
${\hat f_i}$ excluding the phase factor of wave groups is a function of water depth, bottom slope and bottom curvature, which are the same for ![]() ${h_{{I}}}( x )$ and
${h_{{I}}}( x )$ and ![]() $h_{II}( x )$ in
$h_{II}( x )$ in ![]() $x \geq b$. The only difference between
$x \geq b$. The only difference between ![]() ${\hat f_{{I}}}$ and
${\hat f_{{I}}}$ and ![]() $\hat f_{II}$ in
$\hat f_{II}$ in ![]() $x \geq b$ lies in the phase factor and is given by
$x \geq b$ lies in the phase factor and is given by
 \begin{equation} {\hat f_{{I}}}\left( x \right) = {\exp\left({\mathrm{i}\int_a^b {({k_{g,{{I}}}} - {k_{g,{{II}}}})\,\mathrm{d} y} }\right)}{\hat f_{{{II}}}}\left( x \right). \end{equation}
\begin{equation} {\hat f_{{I}}}\left( x \right) = {\exp\left({\mathrm{i}\int_a^b {({k_{g,{{I}}}} - {k_{g,{{II}}}})\,\mathrm{d} y} }\right)}{\hat f_{{{II}}}}\left( x \right). \end{equation} This phase difference in forcing term is also the only difference between the second term of the right-hand side of ![]() $\hat \xi _{g,{{I}}}^+ ( x )$ and
$\hat \xi _{g,{{I}}}^+ ( x )$ and ![]() $\hat \xi _{g,{{II}}}^+ ( x )$ in (D3) for
$\hat \xi _{g,{{II}}}^+ ( x )$ in (D3) for ![]() $x \geq b$, i.e.
$x \geq b$, i.e.
 \begin{equation} \int_b^x {{{\hat \sigma }_{{I}}}\left(\kern0.7pt y \right)\frac{{\hat \xi _{h,{{I}}}^+ \left( x \right)}}{{\hat \xi _{h,{{I}}}^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y} = {\exp\left({\mathrm{i}\int_a^b {({k_{g,{{I}}}} - {k_{g,{{II}}}})\,\mathrm{d} y} }\right)}\int_b^x {{{\hat \sigma }_{{{II}}}}\left(\kern0.7pt y \right)\frac{{\hat \xi _{h,{{II}}}^+ \left( x \right)}}{{\hat \xi _{h,{{II}}}^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y}. \end{equation}
\begin{equation} \int_b^x {{{\hat \sigma }_{{I}}}\left(\kern0.7pt y \right)\frac{{\hat \xi _{h,{{I}}}^+ \left( x \right)}}{{\hat \xi _{h,{{I}}}^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y} = {\exp\left({\mathrm{i}\int_a^b {({k_{g,{{I}}}} - {k_{g,{{II}}}})\,\mathrm{d} y} }\right)}\int_b^x {{{\hat \sigma }_{{{II}}}}\left(\kern0.7pt y \right)\frac{{\hat \xi _{h,{{II}}}^+ \left( x \right)}}{{\hat \xi _{h,{{II}}}^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y}. \end{equation}
This is because, according to (3.7) and (3.10), the forcing term ![]() $\hat f_{i}$ is related to the source field
$\hat f_{i}$ is related to the source field ![]() $\hat \sigma _i$ through a function determined by homogeneous solutions
$\hat \sigma _i$ through a function determined by homogeneous solutions ![]() ${{\hat \xi _{h,i}^ \pm }}$ which are the same in
${{\hat \xi _{h,i}^ \pm }}$ which are the same in ![]() $x \geq b$ for the two topographies considered. Therefore, if the condition
$x \geq b$ for the two topographies considered. Therefore, if the condition
is not satisfied, (D5) and (D6) show that changing the topography in ![]() $a < x < b$ shifts the phase of the downwave subharmonics generated in the subsequent region
$a < x < b$ shifts the phase of the downwave subharmonics generated in the subsequent region ![]() $x \geq b$ through shifting the phase of the forcing field.
$x \geq b$ through shifting the phase of the forcing field.
The non-local influence of surrounding topography at intermediate depth is trivial due to destructive interference of the emitted free subharmonics and the source amplitude determined by radiation stress gradient decreases with water depth as mentioned in Appendix C. In shallow water, the non-local influence becomes non-trivial mainly due to the constructive interference in the full-resonance condition, but also the source amplitude is amplified at shallow water. For instance, Li et al. (Reference Li, Liao, Liu and Zou2020) reported that, when wave groups first propagate across a shoal bathymetry, with the plateau in shallow water, and then transmit into the flat bottom zone connected to it, the transmitted subharmonic is composed of a bound subharmonic and a free subharmonic that is far more energetic than the bound subharmonic. The conceptual model discussed above based on figure 12 suggests that this is because the shallow-water region over the shoal bathymetry functions as a resonator for the downwave-propagating component that amplifies its amplitude by triggering and maintaining the constructive interference process of emitted free subharmonics. On the transmission side of the shoal, where the bottom is flat, this component keeps propagating as a free mode, coexisting with the inherent bound subharmonic described by the Reference Longuet-Higgins and StewartLHS62 solution.
It is also noteworthy that, although the group-induced subharmonic at any observation position ![]() $x$ is essentially dependent on the entire topography on both sides of
$x$ is essentially dependent on the entire topography on both sides of ![]() $x$, for practical computation, the topography and boundary value on either side are sufficient. For example, given the topography and boundary value on the upwave side of
$x$, for practical computation, the topography and boundary value on either side are sufficient. For example, given the topography and boundary value on the upwave side of ![]() $x$, the solution (3.16) can be used. The effect of the topography on the downwave side of
$x$, the solution (3.16) can be used. The effect of the topography on the downwave side of ![]() $x$ is already included in the boundary value
$x$ is already included in the boundary value ![]() $\hat \xi _f^-(a)$ and the effect of group forcing on the upwave-propagating components is manifested by deducting the contribution of sources along the integral path from the overall effect of all sources.
$\hat \xi _f^-(a)$ and the effect of group forcing on the upwave-propagating components is manifested by deducting the contribution of sources along the integral path from the overall effect of all sources.
List of symbols and abbreviations