Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-17T14:18:02.262Z Has data issue: false hasContentIssue false
  • English
  • Français

A two-dimensional vortex condensate at high Reynolds number

Published online by Cambridge University Press:  09 January 2013

Basile Gallet  and
William R. Young
Basile Gallet*
Affiliation:
Scripps Institution of Oceanography, La Jolla, CA 92093-0213, USA
William R. Young
Affiliation:
Scripps Institution of Oceanography, La Jolla, CA 92093-0213, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

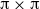We investigate solutions of the two-dimensional Navier–Stokes equation in a $\lrm{\pi} \ensuremath{\times} \lrm{\pi} $ square box with stress-free boundary conditions. The flow is steadily forced by the addition of a source 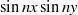$\sin nx\sin ny$ to the vorticity equation; attention is restricted to even $n$ so that the forcing has zero integral. Numerical solutions with 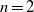$n= 2$ and 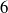$6$ show that at high Reynolds numbers the solution is a domain-scale vortex condensate with a strong projection on the gravest mode, 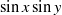$\sin x\sin y$. The sign of the vortex condensate is selected by a symmetry-breaking instability. We show that the amplitude of the vortex condensate has a finite limit as 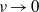$\nu \ensuremath{\rightarrow} 0$. Using a quasilinear approximation we make an analytic prediction of the amplitude of the condensate and show that the amplitude is determined by viscous selection of a particular solution from a family of solutions to the forced two-dimensional Euler equation. This theory indicates that the condensate amplitude will depend sensitively on the form of the dissipation, even in the undamped limit. This prediction is verified by considering the addition of a drag term to the Navier–Stokes equation and comparing the quasilinear theory with numerical solution.

JFM classification

Instability: Instability Instability: Transition to turbulence Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 715 , 25 January 2013 , pp. 359 - 388
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexakis, A. & Doering, C. R. 2006 Energy and enstrophy dissipation in steady state 2D turbulence. Phys. Lett. A 359, 652–657.Google Scholar
Boffetta, S. 2007 Energy and enstrophy fluxes in the double cascade of two-dimensional turbulence. J. Fluid Mech. 589, 253–360.Google Scholar
Chandler, G. J. & Kerswell, R. R. (2012) Simple invariant solutions embedded in two-dimensional Kolmogorov turbulence. J. Fluid Mech. (accepted).CrossRefGoogle Scholar
Chertkov, M., Connaughton, C., Kolokolov, I. & Lebedev, V. 2007 Dynamics of energy condensation in two-dimensional turbulence. Phys. Rev. Lett. 99, 084501.Google Scholar
Chertkov, M., Kolokolov, I. & Lebedev, V. 2010 Universal velocity profile for coherent vortices in two-dimensional turbulence. Phys. Rev. E 81, 015302.Google Scholar
Childress, S. 1979 Alpha effect in flux ropes and sheets. Phys. Earth Planet. Inter. 20, 172–180.CrossRefGoogle Scholar
Cvitanović, P. 1988 Invariant measurement of strange sets in terms of cycles. Phys. Rev. Lett. 61, 24.Google Scholar
Davies, B. 2000 Integral Transforms and Their Applications. Springer.Google Scholar
Fauve, S. & Thual, O. 1990 Solitary waves generated by subcritical instabilities in dissipative systems. Phys. Rev. Lett. 64, 3.Google Scholar
Gallet, B., Herault, J., Laroche, C., Pétrélis, F. & Fauve, S. 2011 Reversals of a large-scale field generated over a turbulent background. Geophys. Astrophys. Fluid Dyn. 106 (4–5), 468–492.CrossRefGoogle Scholar
Gama, S., Vergassola, M. & Frisch, U. 1994 Negative eddy viscosity in isotropically forced two-dimensional flow: linear and nonlinear dynamics. J. Fluid Mech. 260, 95–126.CrossRefGoogle Scholar
Hakim, V., Jakobsen, P. & Pomeau, Y. 1990 Fronts versus solitary waves in nonequilibrium systems. Europhys. Lett. 11, 1.CrossRefGoogle Scholar
Hughes, D. W. & Proctor, M. R. E. 1990 A low-order model of the shear instability of convection: chaos and the effect of noise. Nonlinearity 3, 127–153.CrossRefGoogle Scholar
Kraichnan, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10, 7.Google Scholar
Kumar, K., Pal, P. & Fauve, S. 2006 Critical bursting. Europhys. Lett. 74, 6.Google Scholar
Lilly, D. K. 1969 Numerical simulation of two-dimensional turbulence. Phys. Fluids 12 (Suppl.), II-240.Google Scholar
Maltrud, M. E. & Vallis, G. K. 1991 Energy spectra and coherent structures in forced two-dimensional and beta-plane turbulence. J. Fluid Mech. 228, 321–342.Google Scholar
Meshalkin, L. D. & Sinai, Ya. G. 1961 Investigation of the stability of a stationary solution of a system of equations for the plane movement of an incompressible viscous fluid. J. Appl. Mech. 25, 1700–1705.Google Scholar
Paret, J., Jullien, M.-C. & Tabeling, P. 1999 Vorticity statistics in the two-dimensional enstrophy cascade. Phys. Rev. Lett. 83, 17.Google Scholar
Paret, J. & Tabeling, P. 1997 Experimental observation of the two-dimensional inverse energy cascade. Phys. Rev. Lett. 79, 21.Google Scholar
Rosenbluth, M. N., Berk, H. L., Doxas, I. & Horton, W. 1987 Effective diffusion in laminar convective flows. Phys. Fluids 30, 2636.Google Scholar
Rutgers, M. A. 1998 Forced 2D turbulence: experimental evidence of simultaneous inverse energy and forward enstrophy cascades. Phys. Rev. Lett. 81, 11.CrossRefGoogle Scholar
Sivashinsky, G. I. 1985 Weak turbulence in periodic flows. Physica 17D, 243–255.Google Scholar
Smith, L. & Yakhot, V. 1994 Finite-size effects in forced two-dimensional turbulence. J. Fluid Mech. 274, 115–138.Google Scholar
Sommeria, J. 1986 Experimental study of the two-dimensional inverse energy cascade in a square box. J. Fluid Mech. 170, 139–168.Google Scholar
Thess, A. 1992 Instabilities in two-dimensional spatially periodic flows. Part II: Square eddy lattice. Phys. Fluids A 4, 7.Google Scholar
Tsang, Y.-K. 2010 Non-universal velocity probability densities in forced two-dimensional turbulence: the effect of large-scale dissipation. Phys. Fluids A 22, 115102.Google Scholar
Tsang, Y.-K. & Young, W. R. 2009 Forced-dissipative two-dimensional turbulence: a scaling regime controlled by drag. Phys. Rev. E 79, 045308.Google Scholar