Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T06:22:54.022Z Has data issue: false hasContentIssue false
  • English
  • Français

Two-dimensional nonlinear travelling waves in magnetohydrodynamic channel flow

Published online by Cambridge University Press:  11 November 2014

Jonathan Hagan  and
Jānis Priede
Jonathan Hagan
Affiliation:
Applied Mathematics Research Centre, Coventry University, Priory Street, Coventry CV1 5FB, UK
Jānis Priede*
Affiliation:
Applied Mathematics Research Centre, Coventry University, Priory Street, Coventry CV1 5FB, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This study is concerned with the stability of a flow of viscous conducting liquid driven by a pressure gradient in the channel between two parallel walls subject to a transverse magnetic field. Although the magnetic field has a strong stabilizing effect, this flow, similarly to its hydrodynamic counterpart – plane Poiseuille flow – is known to become turbulent significantly below the threshold predicted by linear stability theory. We investigate the effect of the magnetic field on two-dimensional nonlinear travelling-wave states which are found at substantially subcritical Reynolds numbers starting from 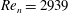$\mathit{Re}_{n}=2939$ without the magnetic field and from 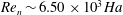$\mathit{Re}_{n}\sim 6.50\times 10^{3}\mathit{Ha}$ in a sufficiently strong magnetic field defined by the Hartmann number 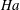$\mathit{Ha}$. Although the latter value is a factor of seven lower than the linear stability threshold 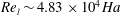$\mathit{Re}_{l}\sim 4.83\times 10^{4}\mathit{Ha}$, it is still more than an order of magnitude higher than the experimentally observed value for the onset of turbulence in magnetohydrodynamic (MHD) channel flow.

JFM classification

Instability: Instability Instability: Nonlinear instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 760 , 10 December 2014 , pp. 387 - 406
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Airiau, C. & Castets, M. 2004 On the amplification of small disturbances in a channel flow with a normal magnetic field. Phys. Fluids 16, 2991–3005.CrossRefGoogle Scholar
Barkley, D. 1990 Theory and predictions for finite-amplitude waves in two-dimensional plane Poiseuille flow. Phys. Fluids 29, 1328–1331.Google Scholar
Bender, C. M. & Orsag, S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers, § 11.4. McGraw-Hill.Google Scholar
Branover, G. G. 1967 Resistance of magnetohydrodynamic channels. Magnetohydrodynamics 3 (4), 1–11.Google Scholar
Brouillette, E. C. & Lykoudis, P. S. 1967 Magneto-fluid-mechanic channel flow. I. Experiment. Phys. Fluids 10, 995–1001.CrossRefGoogle Scholar
Casas, P. S. & Jorba, À. 2012 Hopf bifurcations to quasi-periodic solutions for the two-dimensional plane Poiseuille flow. Commun. Nonlinear Sci. Numer. Simul. 17, 2864–2882.CrossRefGoogle Scholar
Chapman, S. J. 2002 Subcritical transition in channel flows. J. Fluid Mech. 451, 35–97.CrossRefGoogle Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability, § 31.6. Cambridge University Press.Google Scholar
Ehrenstein, U. & Koch, W. 1991 Three-dimensional wavelike equilibrium states in plane Poiseuille flow. J. Fluid Mech. 228, 111–148.Google Scholar
Gerard-Varet, D. 2002 Amplification of small perturbations in a Hartmann layer. Phys. Fluids 14, 1458–1467.CrossRefGoogle Scholar
Hagan, J. & Priede, J. 2013a Capacitance matrix technique for avoiding spurious eigenmodes in the solution of hydrodynamic stability problems by Chebyshev collocation method. J. Comput. Phys. 238, 210–216.CrossRefGoogle Scholar
Hagan, J. & Priede, J. 2013b Weakly nonlinear stability analysis of magnetohydrodynamic channel flow using an efficient numerical approach. Phys. Fluids 25, 124108.CrossRefGoogle Scholar
Hartmann, J. 1937 Hg-dynamics I. Theory of the laminar flow of an electrically conductive liquid in a homogeneous magnetic field. K. Dan. Vidensk. Selsk. Mat. Fys. Medd. 15 (6), 1–28.Google Scholar
Hartmann, J. & Lazarus, F. 1937 Hg-dynamics II. Experimental investigations on the flow of mercury in a homogeneous magnetic field. K. Dan. Vidensk. Selsk. Mat. Fys. Medd. 15 (7), 1–45.Google Scholar
Herbert, T. 1988 Secondary instabilities of boundary layers. Annu. Rev. Fluid Mech. 20, 487–526.CrossRefGoogle Scholar
Hocking, L. M. 1975 Non-linear stability of the asymptotic suction velocity profile. Q. J. Mech. Appl. Maths 28, 341–353.CrossRefGoogle Scholar
Huerre, P. & Rossi, M. 1998 Hydrodynamic instabilities in open flows. In Hydrodynamics and Nonlinear Instabilities (ed. Godreche, C. & Manneville, P.), pp. 81–294. Cambridge University press.CrossRefGoogle Scholar
Kawahara, G., Uhlmann, M. & van Veen, L. 2012 The significance of simple invariant solutions in turbulent flows. Annu. Rev. Fluid Mech. 44, 203–225.CrossRefGoogle Scholar
Kerswell, R. R., Pringle, C. C. T. & Willis, A. P. 2014 An optimisation approach for analysing nonlinear stability with transition to turbulence as an exemplar. Rep. Prog. Phys. 77, 085901.CrossRefGoogle Scholar
Krasnov, D., Thess, A., Boeck, T., Zhao, Y. & Zikanov, O. 2013 Patterned turbulence in liquid metal flow: computational reconstruction of the Hartmann experiment. Phys. Rev. Lett. 110, 084501.CrossRefGoogle ScholarPubMed
Krasnov, D. S., Zienicke, E., Zikanov, O., Boeck, T. & Thess, A. 2004 Numerical study of the instability of the Hartmann layer. J. Fluid Mech. 504, 181–211.CrossRefGoogle Scholar
Lifshits, A. M. & Shtern, V. N. 1980 Monoharmonic analysis of the nonlinear stability of Hartmann flow. Magnetohydrodynamics 15, 243–258.Google Scholar
Likhachev, O. A. 1976 Self-oscillatory flow in asymptotic boundary layers. J. Appl. Mech. Tech. Phys. 17, 194–197.CrossRefGoogle Scholar
Lingwood, R. J. & Alboussière, T. 1999 On the stability of the Hartmann layer. Phys. Fluids 11, 2058–2068.CrossRefGoogle Scholar
Lock, R. C. 1955 The stability of the flow of an electrically conducting fluid between parallel planes under a transverse magnetic field. Proc. R. Soc. Lond. A 233, 105–125.Google Scholar
Moresco, P. & Alboussière, T. 2003 Weakly nonlinear stability of Hartmann boundary layers. Eur. J. Mech. (B/Fluids) 22, 345–353.CrossRefGoogle Scholar
Moresco, P. & Alboussière, T. 2004 Experimental study of the instability of the Hartmann layer. J. Fluid Mech. 504, 167–181.CrossRefGoogle Scholar
Murgatroyd, W. 1953 Experiments in magnetohydrodynamic channel flow. Phil. Mag. 44, 1348–1354.CrossRefGoogle Scholar
Orszag, S. A. & Patera, A. T. 1983 Secondary instability of wall-bounded shear flows. J. Fluid Mech. 128, 347–385.CrossRefGoogle Scholar
Peyret, R. 2002 Spectral Methods for Incompressible Viscous Flow. Springer.CrossRefGoogle Scholar
Pothérat, A. 2007 Quasi two-dimensional perturbations in duct flows with a transverse magnetic field. Phys. Fluids 19, 74104.CrossRefGoogle Scholar
Pugh, J. D. & Saffman, P. G. 1988 Two-dimensional superharmonic stability of finite amplitude waves in plane Poiseuille flow. J. Fluid Mech. 194, 295–307.CrossRefGoogle Scholar
Reynolds, W. C. & Potter, M. C. 1967 Finite-amplitude instability of parallel shear flows. J. Fluid Mech. 27, 465–492.CrossRefGoogle Scholar
Roberts, P. H. 1967 An Introduction to Magnetohydrodynamics, § 6.2. Longmans.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows, § 5.3. Springer.CrossRefGoogle Scholar
Soibelman, I. & Meiron, D. I. 1991 Finite-amplitude bifurcations in plane Poiseuille flow: two-dimensional Hopf bifurcation. J. Fluid Mech. 229, 389–416.CrossRefGoogle Scholar
Takashima, M. 1996 Stability of the modified plane Poiseuille flow in the presence of a magnetic field. Fluid Dyn. Res. 17, 293–310.CrossRefGoogle Scholar
Waleffe, F. 1995 Transition in shear flows: non-linear normality versus non-normal linearity. Phys. Fluids 7, 3060–3066.CrossRefGoogle Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.CrossRefGoogle Scholar
Yaglom, A. M. 2012 Hydrodynamic Instability and Transition to Turbulence (ed. Frisch, U.), Springer.CrossRefGoogle Scholar
Zikanov, O., Krasnov, D., Boeck, Th., Andre Thess, A. & Rossi, M. 2014 Laminar–turbulent transition in magnetohydrodynamic duct, pipe, and channel flows. Appl. Mech. Rev. 66, 030802.CrossRefGoogle Scholar
Zinov’ev, A. T. & Shtern, V. N. 1987 Self-exited oscillations in Hartmann channel and boundary-layer flows. Magnetohydrodynamics 23, 24–30.Google Scholar