Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kumar, Pritam
Sourav, Kumar
Kumar, Deepak
and
Sen, Subhankar
2017.
Wake-Induced Vibrations of Tandem Circular Cylinders of Different Diameters.
SSRN Electronic Journal ,
Bhatt, Rajesh
and
Alam, Md. Mahbub
2018.
Vibrations of a square cylinder submerged in a wake.
Journal of Fluid Mechanics,
Vol. 853,
Issue. ,
p.
301.
Kim, Junyoung
Song, Minho
and
Kim, Daegyoum
2018.
Large-amplitude flow-induced vibration of cylindrical pendulums.
Journal of Fluids and Structures,
Vol. 79,
Issue. ,
p.
39.
Zhang, Meihua
and
Zheng, Zhongquan C.
2018.
Relations of POD modes and Lyapunov exponents to the nonlinear dynamic states in flow over oscillating tandem cylinders.
Physics of Fluids,
Vol. 30,
Issue. 12,
p.
123602.
Qin, Bin
Alam, Md. Mahbub
Ji, Chunning
Liu, Yang
and
Xu, Shengjin
2018.
Flow-induced vibrations of two cylinders of different natural frequencies.
Ocean Engineering,
Vol. 155,
Issue. ,
p.
189.
Alam, Md. Mahbub
Elhimer, Mehdi
Wang, Longjun
Jacono, David Lo
and
Wong, C. W.
2018.
Vortex shedding from tandem cylinders.
Experiments in Fluids,
Vol. 59,
Issue. 3,
Zafar, Farhan
and
Alam, Md. Mahbub
2018.
A low Reynolds number flow and heat transfer topology of a cylinder in a wake.
Physics of Fluids,
Vol. 30,
Issue. 8,
Gao, Yangyang
Yang, Kang
Zhang, Baofeng
Cheng, Kaiyu
and
Chen, Xinping
2019.
Numerical investigation on vortex-induced vibrations of four circular cylinders in a square configuration.
Ocean Engineering,
Vol. 175,
Issue. ,
p.
223.
Huera-Huarte, F.J.
and
Jiménez-González, J.I.
2019.
Effect of diameter ratio on the flow-induced vibrations of two rigidly coupled circular cylinders in tandem.
Journal of Fluids and Structures,
Vol. 89,
Issue. ,
p.
96.
Qin, Bin
Alam, Md. Mahbub
and
Zhou, Yu
2019.
Free vibrations of two tandem elastically mounted cylinders in crossflow.
Journal of Fluid Mechanics,
Vol. 861,
Issue. ,
p.
349.
Shang, Jingmiao
Zhou, Qiang
Alam, Md. Mahbub
Liao, Haili
and
Cao, Shuyang
2019.
Numerical studies of the flow structure and aerodynamic forces on two tandem square cylinders with different chamfered-corner ratios.
Physics of Fluids,
Vol. 31,
Issue. 7,
Derakhshandeh, J.F.
and
Alam, Md Mahbub
2019.
A review of bluff body wakes.
Ocean Engineering,
Vol. 182,
Issue. ,
p.
475.
Zhou, Qiang
Alam, Md. Mahbub
Cao, Shuyang
Liao, Haili
and
Li, Mingshui
2019.
Numerical study of wake and aerodynamic forces on two tandem circular cylinders at Re = 103.
Physics of Fluids,
Vol. 31,
Issue. 4,
Chen, Zhenlin
Alam, Md. Mahbub
Qin, Bin
and
Zhou, Yu
2020.
Energy harvesting from and vibration response of different diameter cylinders.
Applied Energy,
Vol. 278,
Issue. ,
p.
115737.
Zhu, Hongjun
Tan, Xiaonian
Gao, Yun
Zhou, Tongming
and
Liu, Wenli
2020.
Two-degree-of-freedom flow-induced vibration of two rigidly coupled tandem cylinders of unequal diameters.
Ocean Engineering,
Vol. 216,
Issue. ,
p.
108142.
Lin, Ke
Wang, Jiasong
Zheng, Hanxu
and
Sun, Yuankun
2020.
Numerical investigation of flow-induced vibrations of two cylinders in tandem arrangement with full wake interference.
Physics of Fluids,
Vol. 32,
Issue. 1,
Gao, Yangyang
Zhang, Yanming
Zhao, Ming
and
Wang, Lizhong
2020.
Numerical investigation on two degree-of-freedom flow-induced vibration of three tandem cylinders.
Ocean Engineering,
Vol. 201,
Issue. ,
p.
107059.
Bakhtiari, A.
Zeinoddini, M.
Ashrafipour, H.
Tamimi, V.
Harandi, M.M. Aalami
and
Jadidi, P.
2020.
The effects of marine fouling on the wake-induced vibration of tandem circular cylinders.
Ocean Engineering,
Vol. 216,
Issue. ,
p.
108093.
Chen, Guanghao
Alam, Md. Mahbub
and
Zhou, Yu
2020.
Dependence of added mass on cylinder cross-sectional geometry and orientation.
Journal of Fluids and Structures,
Vol. 99,
Issue. ,
p.
103142.
Xu, Wanhai
Zhang, Qiannan
Lai, Jiang
Wang, Qicheng
and
Yu, Yang
2020.
Flow-induced vibration of two staggered flexible cylinders with unequal diameters.
Ocean Engineering,
Vol. 211,
Issue. ,
p.
107523.
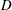 $D$ placed in the wake of a fixed cylinder of smaller diameter
$D$ placed in the wake of a fixed cylinder of smaller diameter 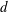 $d$. The ratios
$d$. The ratios  $d/D$ and
$d/D$ and 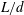 $L/d$ are varied from 0.2 to 1.0 and from 1.0 to 5.5, respectively, where
$L/d$ are varied from 0.2 to 1.0 and from 1.0 to 5.5, respectively, where 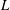 $L$ is the distance between the centre of the upstream cylinder to the forward stagnation point of the downstream cylinder. Extensive measurements are conducted to capture the cylinder vibration and frequency responses, surface pressure, shedding frequencies and flow fields using laser vibrometer, hot-wire, pressure scanner and particle image velocimetry techniques. Six distinct flow regimes are identified. It has been found that a violent vibration may erupt for the spring-supported cylinder, and its dependence on
$L$ is the distance between the centre of the upstream cylinder to the forward stagnation point of the downstream cylinder. Extensive measurements are conducted to capture the cylinder vibration and frequency responses, surface pressure, shedding frequencies and flow fields using laser vibrometer, hot-wire, pressure scanner and particle image velocimetry techniques. Six distinct flow regimes are identified. It has been found that a violent vibration may erupt for the spring-supported cylinder, and its dependence on 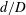 $d/D$ and
$d/D$ and 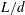 $L/d$ is documented. A careful examination and analysis of the flow structure, along with the simultaneously captured pressure distribution around and vibration of the downstream cylinder, cast light upon the mechanisms behind this vibration and its sustainability. The roles of added mass, flow-induced damping and physical aspects in the process of initiating the vibration are discussed in detail.
$L/d$ is documented. A careful examination and analysis of the flow structure, along with the simultaneously captured pressure distribution around and vibration of the downstream cylinder, cast light upon the mechanisms behind this vibration and its sustainability. The roles of added mass, flow-induced damping and physical aspects in the process of initiating the vibration are discussed in detail.


