Twin forces: similarity between rotation and stratification effects on wall turbulence

Abstract

Can the similarity between rotation and stratification provide quantitative predictions for complex turbulence? In this work, we focus on plane Couette turbulence as the background flow, which allows us to eliminate the key differences between Rayleigh–Bénard and Taylor–Couette turbulence, and facilitates a quantitative mapping across many complex turbulent systems involving rotation, stratification and curvature effects. To characterize the separated or coupled effects of rotation and stratification, we introduce an overall Richardson number ${Ri}_\chi$ which is the sum of the Coriolis Richardson number $Ri_\theta$ and the buoyancy Richardson number $Ri_T$. When the Prandtl number $Pr=1$, the heat and inertial-frame momentum transport almost coincide and mainly depend on ${Ri}_\chi$ and the Reynolds number, regardless of the specific ratio between $Ri_\theta$ and $Ri_T$. When $Pr$ varies, the weighted average ${Nu}_\chi$ of the transport coefficients can still remain approximately invariant in most cases. Furthermore, the large-scale structures in purely rotating and purely stratified cases exhibit strikingly similar features. These findings not only indicate a more reasonable analogy for the ultimate Taylor–Couette turbulence but also pave the way for developing new predictive models for natural and industrial processes.

1. Introduction

Rotating and stratified flows are prevalent in various turbulent systems, ranging from the Earth's atmosphere (Wyngaard 1992; Hartmann, Moy & Fu 2001) and celestial bodies (Young & Read 2017; Schumacher & Sreenivasan 2020) to turbomachinery (Han 2018; You et al. 2018). In celestial bodies, for instance, the Coriolis force significantly influences buoyancy-driven flows (Wyngaard 1992; Young & Read 2017; Schumacher & Sreenivasan 2020), whereas in high-temperature turbines, the buoyancy force has a substantial impact on rotating flows (Han 2018; You et al. 2018). The coupling effects of the Coriolis and buoyancy forces are perfectly illustrated in the Earth's global atmospheric circulation with Hadley, Ferrel and polar cells (Lutgens, Tarbuck & Tasa 2007). Therefore, it is essential to consider both the isolated and combined effects of rotation and stratification in these systems.

A possible approach to better understand these complex effects is the analogy between rotating wall turbulence and buoyancy-driven turbulence (Jeffreys 1928; Bradshaw 1969; Veronis 1970; Lezius & Johnston 1976; Tanaka et al. 2000; Busse 2012; Ostilla-Mónico et al. 2014; Brauckmann, Eckhardt & Schumacher 2017; Zhang et al. 2019; Eckhardt, Doering & Whitehead 2020; Brethouwer 2021; Zhang, Xia & Chen 2022). One of the most well-known examples is the analogy between Taylor–Couette flow (Taylor 1923; van Gils et al. 2011; Huisman et al. 2012; Grossmann, Lohse & Sun 2016; Zhu et al. 2018) and Rayleigh–Bénard convection (Kraichnan 1962; Ahlers, Grossmann & Lohse 2009; Lohse & Xia 2010; Grossmann & Lohse 2011; Zhu et al. 2019; Wang, Zhou & Sun 2020; Jiang et al. 2022), which are referred to as ‘the twins of turbulence research’ by Busse (2012). These two systems exhibit similar ultimate scaling of heat or angular momentum transport and Reynolds number (van Gils et al. 2011; Huisman et al. 2012; Zhu et al. 2018, 2019; Jiang et al. 2022), and their turbulent statistics and flow structures are also similar when their transport coefficients (angular momentum for Taylor–Couette and heat for Rayleigh–Bénard) are chosen to be consistent (Brauckmann et al. 2017). However, the analogy is found to only hold in a qualitative way, particularly for the prediction of the transition parameters of the different systems. This is mainly caused by two differences between these two systems. First, it is easier for the Taylor–Couette system to have a turbulent boundary layer due to wall shear, while the Rayleigh–Bénard system can only achieve boundary layer transition indirectly through the buoyancy effect (Grossmann et al. 2016). Second, although both the ideal Taylor–Couette system (infinitely long cylinders) and the ideal Rayleigh–Bénard system (infinitely large plates) are statistically homogeneous in the directions perpendicular to the wall-normal direction, they are very different in isotropy. Statistically, the Rayleigh–Bénard system exhibits horizontal isotropy, while the Taylor–Couette system is not isotropic in the azimuthal-axial hyperplanes even in the limit of vanishing curvature.

Fortunately, in many realistic stratified flows, stratification is coupled with wall shear (Prandtl 1932; Obukhov 1946; Monin & Obukhov 1954; Kader & Yaglom 1990; Deusebio, Caulfield & Taylor 2015; Pirozzoli et al. 2017; Zhou, Taylor & Caulfield 2017; Haghshenas & Mellado 2019; Blass et al. 2020, 2021), effectively eliminating the two primary differences. To be specific, adding a mean shear to the Rayleigh–Bénard system not only makes it easier to achieve boundary layer transition, but also breaks the horizontal isotropy. Therefore, investigating the effects of rotation and stratification in wall-sheared flows can help upgrade the qualitative analogy into a quantitative prediction approach.

The analogy between two systems can be further extended to the analogy between the rotation and stratification effect, and also the analogy between heat and momentum transfer in rotating stratified wall turbulence. These analogies can provide a more comprehensive understanding of the dynamics of complex wall turbulence. Since the limiting case of Taylor–Couette flow with vanishing curvature is the spanwise rotating plane Couette flow (Faisst & Eckhardt 2000; Dubrulle et al. 2005; Brauckmann, Salewski & Eckhardt 2016), and the Rayleigh–Bénard convection with wall shear can be called stratified plane Couette flow, it is straightforward to choose plane Couette turbulence as the background flow to investigate both rotation and stratification effects. In addition, essentially identical boundary conditions of velocity and temperature can be applied to plane Couette turbulence, making it convenient to examine the analogy between heat and momentum transfer in the same case. The analogy between the rotation and stratification effect can be examined through the comparison between two cases with different combinations of rotation and stratification.

In this work, we investigate the turbulence statistics and large-scale flow structures in plane Couette turbulence subject to rotation or stratification, or combinations of both effects. The basic equations and mathematical basis of thermal analogy, followed by redefined physical parameters and our theoretical conjectures, are introduced in § 2. The conjectures are then examined and rectified with previous and newly obtained numerical simulation results in § 3. Finally, the present work will be summarized in § 4.

2. Governing equations and theoretical conjectures

2.1. Original equations

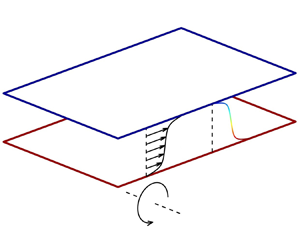
As shown in figure 1, the $x$, $y$ and $z$ axes with corresponding unit vectors $\hat {\boldsymbol {x}}$, $\hat {\boldsymbol {y}}$ and $\hat {\boldsymbol {z}}$ represent the streamwise, wall-normal and spanwise directions, respectively. We denote the streamwise velocity and temperature difference between two walls as $[U]$ and $[T]$, the distance between the walls as $H$, the gravitational acceleration as $-g\hat {\boldsymbol {y}}$, the angular velocity as $\varOmega \hat {\boldsymbol {z}}$, the thermal expansion coefficient as $\beta$, the kinematic viscosity as $\nu$ and thermal diffusion coefficient as $\alpha$. The centrifugal buoyancy is not shown explicitly mainly because the effect of centrifugal force induced by the Earth's rotation is embedded in the shape of the Earth and locally measured values of gravitational acceleration. In addition, centrifugal buoyancy in a rapidly rotating Taylor–Couette device with a large radius ratio can serve as a wall-normal ‘gravity’ (Jiang et al. 2022). There are four independent control parameters: the Reynolds number ${Re}=[U]H/\nu$, the rotation number ${R_\varOmega }=2\varOmega H/[U]$, the Rayleigh number ${Ra}=g\beta [T]H^3/\nu \alpha$ and the Prandtl number ${Pr}=\nu /\alpha$. Under the Boussinesq approximation (Boussinesq 1903), the non-dimensionalized basic equations are as follows:

(2.1a)$$\begin{gather} \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{u}=0, \end{gather}$$

(2.1b)$$\begin{gather}\frac{\partial\boldsymbol{u}}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{u} ={-}\boldsymbol{\nabla} p+\frac{1}{Re}\nabla^2\boldsymbol{u} +{R_\varOmega}\boldsymbol{u}\times\hat{\boldsymbol{z}} +\frac{Ra}{Re^2Pr}T\hat{\boldsymbol{y}}, \end{gather}$$

(2.1c)$$\begin{gather}\frac{\partial T}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{\nabla} T=\frac{1}{RePr}\nabla^2 T, \end{gather}$$

where the boundary conditions are $\boldsymbol {u}|_{y=\pm 0.5}=\pm 0.5\hat {\boldsymbol {x}}$ and $T|_{y=\pm 0.5}=\mp 0.5$.

Figure 1. Sketch of spanwise rotating stratified plane Couette flow.

2.2. Thermal analogy

For spanwise rotating shear flows, a variable transformation (Tanaka et al. 2000; Zhang et al. 2019) indicates that the Coriolis force has a buoyancy-like effect on the wall-normal velocity. We can extend this variable transformation to the present rotating stratified system, which reveals a striking similarity between the effects of the Coriolis and buoyancy forces characterized respectively by ${R_\varOmega }$ and ${Ra}$. Specifically, by defining $\theta =({R_\varOmega }y-u)/(1-{R_\varOmega })$, the streamwise and wall-normal momentum equations can be expressed as follows (detailed derivations are shown in Appendix A):

(2.2a)$$\begin{gather} \frac{\partial\theta}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{\nabla}\theta =\frac{1}{1-{R_\varOmega}}\frac{\partial\tilde{p}}{\partial x} +\frac{1}{Re}\nabla^2\theta, \end{gather}$$

(2.2b)$$\begin{gather}\frac{\partial v}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{\nabla} v ={-}\frac{\partial\tilde{p}}{\partial y}+\frac{1}{Re}\nabla^2 v +{R_\varOmega}(1-{R_\varOmega})\theta +\frac{Ra}{Re^2Pr}T, \end{gather}$$

where $\tilde {p}=p+{R_\varOmega ^2}y^2/2$. Notably, the boundary condition of $\theta$ coincides with that of the temperature $T$, and the streamwise component of the Coriolis force is absorbed into the convection term of $\theta$. We observe that the transformed equations establish a close analogy between $\theta$ and a temperature/concentration field with Prandtl/Schmidt number being $1$ and Rayleigh number being ${Re}^2{R_\varOmega }(1-{R_\varOmega })$. An apparent difference between $\theta$ and a temperature/concentration field is that $\theta$ has a source term arising from the incompressible constraint on velocity. This is because the incompressible condition requires a full elimination of the divergence and wall-normal flux of $\partial \boldsymbol {u}/\partial t$ by the pressure gradient $\boldsymbol {\nabla } p$, whose streamwise component appears as a source term in the $\partial \theta /\partial t$ equation.

2.3. Theoretical conjectures

Taking inspiration from the transformed variables and equations, we propose parameter transformations for the rotation number and Rayleigh number. Based on previous research on sheared Rayleigh–Bénard convection at different Prandtl numbers (Blass et al. 2021), we define the buoyancy Richardson number ${Ri}_T$ as ${Ra}/{Re}^2$ for ${Pr}\leq 1$ and ${Ra}{Pr}/{Re}^2$ for ${Pr}>1$ (explained later in this subsection). The Coriolis Richardson number is defined as ${Ri}_\theta ={R_\varOmega }(1-{R_\varOmega })$. In classical Taylor–Couette systems with fixed outer cylinder and radius ratio larger than $1/2$, the angular velocity of the characteristic rotating system does not exceed a quarter of the spatially averaged rotating-frame vorticity, resulting in ${R_\varOmega }\leq 0.5$ (Dubrulle et al. 2005; Brauckmann et al. 2016). We are focusing on the same $R_\varOmega$ range, which ensures that there is a one-to-one mapping between $(Re,Pr,{Ri}_T,{Ri}_\theta )$ and $(Re,Pr,{Ra},{R_\varOmega })$ in the present study. Correspondingly, we define the heat Nusselt number as ${Nu}_T=-d\langle T\rangle /{{\rm d} y}|_{\pm 0.5}$ and the momentum Nusselt number as ${Nu}_\theta =-d\langle \theta \rangle /{{\rm d} y}|_{\pm 0.5}$. It should be noted that ${Nu}_\theta$ characterizes the streamwise momentum transport in the inertial frame.

Furthermore, we define an overall Richardson number and the relative stratification-rotation difference as

(2.3a,b)\begin{equation} {Ri}_\chi={Ri}_T+{Ri}_\theta,\quad \gamma=\frac{{Ri}_T-{Ri}_\theta}{{Ri}_T+{Ri}_\theta}, \end{equation}

which can replace ${Ri}_T$ and ${Ri}_\theta$ when ${Ri}_\chi \neq 0$. Our choice of defining ${Ri}_\chi$ is motivated by our goal to unify the effects of the Coriolis and buoyancy forces, while $\gamma$ quantifies the relative contributions of the two forces. More specifically, we expect that ${Ri}_\chi$ consists of $50(1+\gamma )$ percent stratification effect and $50(1-\gamma )$ percent rotation effect. Correspondingly, an overall Nusselt number is defined as the weighted average

(2.4)\begin{equation} {Nu}_\chi=\frac{1+\gamma}{2}{Nu}_T+\frac{1-\gamma}{2}{Nu}_\theta, \end{equation}

of heat and momentum Nusselt numbers, where the weights of heat and momentum transport are proportional to the contributions of the stratification and rotation effect, respectively.

In the special case of $Pr=1$, we can define a mixed scalar

(2.5)\begin{equation} \chi=\frac{1+\gamma}{2}T+\frac{1-\gamma}{2}\theta, \end{equation}

which has the same boundary condition as those of $T$ and $\theta$. The evolution of $T$ and $\theta$ should be very similar because the diffusivity of $\theta$ is the same as that of $T$, and the ensemble average of the source term of $\theta$ is $(1-R_\varOmega )^{-1}\langle \partial \tilde {p}/\partial x\rangle =0$. Therefore, it is reasonable to conjecture that $\theta \approx T\approx \chi$ at $Pr=1$, which we call as the inertial-frame Reynolds analogy. Under such conjecture, the Coriolis and buoyancy term in (2.2b) can be approximately unified into an overall buoyancy-like term:

(2.6)\begin{equation} {{R_\varOmega}(1-{R_\varOmega})\theta+\frac{Ra}{Re^2Pr}T \approx\left[{R_\varOmega}(1-{R_\varOmega})+\frac{Ra}{Re^2Pr}\right]\chi =Ri_\chi \chi}, \end{equation}

which perfectly demonstrates the adequacy of defining $Ri_\chi$.

Motivated by the mathematical analogy between the Coriolis and buoyancy effects, we propose another compelling conjecture that the heat and momentum Nusselt numbers, ${Nu}_T$ and ${Nu}_\theta$, respectively, are primarily governed by the Reynolds number ${Re}$ and the overall Richardson number ${Ri}_\chi$, with little sensitivity to $\gamma$ and ${Pr}$. In essence, we anticipate that in the plane Couette system, the Coriolis and buoyancy forces exert nearly identical influences, if not entirely indistinguishable, on both heat and momentum transport. Following the reference of ‘the twins’ to Taylor–Couette and Rayleigh–Bénard systems (Busse 2012), we call the second conjecture the twin-force analogy.

The piecewise definition of $Ri_T$ is motivated by the twin-force analogy. Such analogy is likely to hold for $Pr=1$, which means that $Nu_\theta |_{\gamma =-1}=Nu_\chi |_{\gamma =-1}\approx Nu_\chi |_{\gamma =+1}=Nu_T|_{\gamma =+1}$ at $Pr=1$, and fixed $Re$ and $Ri_\chi$. Since $Nu_\theta$ in a rotating plane Couette system ($\gamma =-1$) does not depend on the Prandtl number $Pr$, it is necessary to make $Nu_T$ in a sheared Rayleigh–Bénard system ($\gamma =+1$) almost independent on $Pr$ to extend the conjecture to systems with $Pr\neq 1$. This requires a proper definition of $Ri_T$. The results of Blass et al. (2021) show that the influence of $Pr$ on heat transport in sheared Rayleigh–Bénard convection is relatively small when $Pr<1$ and considerable when $Pr>1$. Furthermore, when $Pr>1$, the thermal boundary layer should be embedded in the momentum boundary layer in sheared Rayleigh–Bénard convection, which indicates that the influence of viscosity is less important and that $Ra$ can be replaced with $RaPr$ in which $\nu$ is absent. The appropriateness of such a definition will be examined by simulation results in the next section.

3. Numerical results and discussions

3.1. Previous results

Previous studies on rotating plane Couette flow (Bech & Andersson 1996, 1997; Tillmark & Alfredsson 1996; Alfredsson & Tillmark 2005; Tsukahara, Tillmark & Alfredsson 2010; Gai et al. 2016; Huang et al. 2019; Huang, Xia & Chen 2020; Brethouwer 2021) and sheared Rayleigh–Bénard convection (Blass et al. 2020, 2021) may provide some evidence for the validity of our conjectures. Figure 2 shows $Nu_\theta$ and $Nu_T$ from direct numerical simulations at different $Re\in [4000,40\,000]$, $\gamma =\pm 1$ and $Ri_\chi$. The results of rotating plane Couette flow ($\gamma =-1$) at five different $Re$ are from Huang et al. (2020) (without heat transfer data) and Brethouwer (2021, 2023), while those of sheared Rayleigh–Bénard convection ($\gamma =+1$) at six different $Re$ are from Blass et al. (2020). Different normalized efficiencies of momentum transport (friction Reynolds numbers and rotating-frame momentum Nusselt numbers) are transformed into $Nu_\theta$ following the relations derived in Appendix B.

Figure 2. Momentum Nusselt number $Nu_\theta$ ($\square$ with solid lines) and heat Nusselt number $Nu_T$ ($\Diamond$ with dashed lines) as functions of overall Richardson number ${Ri}_\chi$ in both rotating plane Couette flow ($\gamma =-1$, solid symbols) and sheared Rayleigh–Bénard convection ($\gamma =+1$, hollow symbols) at different $Pr=1$, and (a) $Re<10\,000$ and (b) $Re>10\,000$. Data are from Huang et al. (2020), Blass et al. (2020), Brethouwer (2021, 2023).

The first apparent phenomenon is that $Nu_\theta$ is close to $Nu_T$ in the same case, and the relative difference between them is $O(10\,\%)$ when $Ri_\chi <0.25$. This strongly supports the validity of the inertial-frame Reynolds analogy (which reduces to the classical Reynolds analogy when $R_\varOmega =0$), as can also be indicated by the analysis of rotating wall turbulence performed by Zhang et al. (2019), Brethouwer (2021, 2023). With more detailed observation, it can be seen that the turbulence enhanced by stratification ($\gamma =+1$) is usually more efficient in heat transport than (inertial-frame) momentum transport, and the turbulence enhanced by rotation ($\gamma =-1$) is usually more efficient in momentum transport. Figure 2 also shows that a rotating system and a stratified system at similar $Re$ and $Ri_\chi$ would have almost equally similar $Nu_\theta$ and $Nu_T$, which indicates the validity of the twin-force analogy.

However, figure 2 only supports our conjectures at $Pr=1$ and $\gamma =\pm 1$, where only one of the rotation and stratification effects appears in each case. Further examinations and discussions for more arbitrary combinations of rotation and stratification in a wide range of $Pr$ should be carried out.

3.2. Present results

To quantitatively test our conjectures in more complex conditions, we performed direct numerical simulations using the open-source spectral element code NEK5000 at ${Re}\in \{5000,10\,000\}$, ${Pr}\in \{1,4^{\pm 1}\}$, ${Ri_\chi }\in \{0,0.04,0.16\}$ and $\gamma \in \{0,\pm 1,\pm 2\}$. The computational domain used in this study is $L_x\times L_y\times L_z=9{\rm \pi} \times 1\times 4{\rm \pi}$, and it is accompanied by an equivalent grid size $n_x\times n_y\times n_z$ of $568\times 71\times 505$ for $Re=5000$ and $1072\times 106\times 617$ for $Re=10\,000$. More computational set-ups and validation procedures are detailed in Appendix C. Physical parameters, along with the computed heat, momentum and overall Nusselt numbers, are shown in table 1.

Table 1. Parameters used in the present study, along with the computed heat, momentum and overall Nusselt numbers.

Figure 3 shows the heat, momentum and overall Nusselt numbers of plane Couette systems in statistically steady state at ${Pr}=1$ and at different values of $Re$, ${Ri}_\chi$ and $\gamma$. It is worth noting that the relative stratification-rotation difference, $\gamma$, serves as a useful classification parameter for the system, dividing it into five distinct types: stable stratification and unstable rotation ($\gamma <-1$), purely unstable rotation ($\gamma =-1$), unstable stratification and unstable rotation ($-1<\gamma <+1$), purely unstable stratification ($\gamma =+1$), and unstable stratification and stable rotation ($\gamma >+1$). Although the large-scale patterns in statistically steady states can be different under different initial conditions, it can be indicated from Huang et al. (2019, 2020) that the resulting variations in heat and momentum transfer are usually acceptable in the following discussions. In addition, all cases at the same $Re$ and $Ri_\chi \neq 0$ are initiated with the same velocity and temperature field, which can reduce the difference of flow state between two neighbouring cases with similar $\gamma$.

Figure 3. Heat Nusselt number ${Nu}_T$, momentum Nusselt number ${Nu}_\theta$ and overall Nusselt number ${Nu}_\chi$ as functions of the overall Richardson number ${Ri}_\chi$ and the relative stratification-rotation difference $\gamma$ for plane Couette flow at $Pr=1$, and (a) $Re=5000$ and (b) $Re=10\,000$. The red and blue lines denote the heat and momentum Nusselt numbers, respectively, at the condition of ${Ri}_T={Ri}_\theta =0$.

In figure 3, we observe that for ${Pr}=1$, the values of ${Nu}_T$ and ${Nu}_\theta$ are relatively close to each other in the same system. This indicates the validity of our first conjecture in § 2.3, namely the inertial-frame Reynolds analogy, when complex combinations of rotation and stratification are present. The validity of the inertial-frame Reynolds analogy at $R_\varOmega \neq 0$ straightforwardly implies the invalidity of the classical Reynolds analogy calculated from rotating-frame momentum transfer (Brethouwer 2018), as indicated by Zhang et al. (2019) and Brethouwer (2021, 2023). An explanation based on the Lagrangian view proposed by Zhang et al. (2019) is helpful for understanding: under spanwise system rotation, the evolution of the rotating-frame streamwise velocity carried by vertical motions can be written as

(3.1)\begin{equation} \frac{{\rm d} u}{{\rm d} t}\approx R_\varOmega v+\zeta=R_\varOmega\frac{{\rm d} y}{{\rm d} t}+\zeta,\end{equation}

where $\zeta$ denotes the contributions from other terms in the momentum equation and could be regarded as a stochastic forcing. In other words, when the Coriolis force is present, the inertial-frame streamwise velocity $u-R_\varOmega y$ is much more similar to a temperature field than the rotating-frame streamwise velocity $u$.

The deviation of $Nu_\theta$ and $Nu_T$ from the inertial-frame Reynolds analogy is small, but increases to $O(10\,\%)$ at $Ri_\chi =0.16$ and $\gamma =\pm 2$ for both $Re=5000$ and $Re=10\,000$. There is $Nu_\theta >Nu_T$ when $Ri_\theta >0>Ri_T$, and $Nu_T>Nu_\theta$ when $Ri_T>0>Ri_\theta$. This is consistent with the previous simulation results (figure 2). A possible reason is that rotation-induced flow structures are more efficient for momentum transport, while buoyancy-induced flow structures are more efficient for heat transport. The difference in flow structures can be indicated in the difference between the Coriolis and buoyancy effects on vorticity:

(3.2a)$$\begin{gather} \boldsymbol{\nabla}\times(R_\varOmega\boldsymbol{u}\times\hat{\boldsymbol{z}}) \leftrightarrow R_\varOmega i\boldsymbol{k}\times (\check{\boldsymbol{u}}\times\hat{\boldsymbol{z}}) =iR_\varOmega(1-R_\varOmega)\left({-}k_z\check{\theta}, \frac{k_z\check{v}}{1-R_\varOmega},\frac{k_z\check{w}}{1-R_\varOmega}\right), \end{gather}$$

(3.2b)$$\begin{gather}\boldsymbol{\nabla}\times\left(\frac{Ra}{Re^2Pr}T\hat{\boldsymbol{y}}\right) \leftrightarrow i\boldsymbol{k}\times\hat{\boldsymbol{y}}\frac{Ra}{Re^2Pr}\check{T} =i\frac{Ra}{Re^2Pr}({-}k_z\check{T},0,k_x\check{T}), \end{gather}$$

where $\boldsymbol {k}=(k_x,k_y,k_z)$ denotes the spatial wavenumber and $\check {\varphi }(\boldsymbol {k})$ denotes the spatial Fourier transform of $\varphi (\boldsymbol {x})$. The last equality of (3.2a) is obtained using the incompressible condition $i\boldsymbol {k}\boldsymbol{\cdot}\check {\boldsymbol {u}}=0$ and the fact that $k_z\check {y}\equiv 0$. Therefore, even if $Pr=1$ and $\theta =T$ everywhere, only the streamwise curl of the summed force can be unified into $-Ri_\chi k_z\check {\chi }$.

More importantly, at the same ${Ri}_\chi$, we find in figure 3 that $\gamma$ only has very small influence on the three Nusselt numbers, thus verifying the twin-force analogy for ${Pr}=1$ situations. This indicates that the Coriolis and buoyancy forces have almost the same effect on turbulent transport, especially for purely stratified ($\gamma =+1$) or purely rotating ($\gamma =-1$) cases. Furthermore, they can easily superpose when their Richardson numbers have the same sign ($|\gamma |<1$), and partially counteract when their Richardson numbers have opposite signs ($|\gamma |>1$).

In the case of $Re=5000$ and ${Pr}=1$, there is a small decrease of both heat and momentum Nusselt numbers for $\gamma \geq -1$. It can be attributed to the suppression effect of wall shear on plumes. By using the variable transformation given in (2.2a), the momentum Nusselt number can be related to the normalized average wall shear, which can be called as the rotating-frame momentum Nusselt number and given by

(3.3)\begin{equation} \left.\frac{{\rm d} \langle u\rangle}{{\rm d} y}\right|_{\pm0.5}={Nu}_\theta -\frac{1-\sqrt{1-2(1-\gamma){Ri}_\chi}}{2} ({Nu}_\theta-1). \end{equation}

Therefore, a nearly constant ${Nu}_\theta$ leads to an increase of wall shear with $\gamma$, resulting in a stronger suppression effect on plumes and consequently a suppression of heat and momentum transfer. When $Re$ increases to $10\,000$, the decrease of $Nu_T$ and $Nu_\theta$ is almost negligible, indicating that the velocity fluctuations enhanced by wall shear begin to compensate the suppression effect on plume activity. Similar effects of wall shear can be inferred from Blass et al. (2020), which shows that $Nu_T$ at fixed $Ra$ first decreases and then increases with increasing $Re$. At $Re=10\,000$, the deviation from the twin-force analogy becomes relatively larger, which can be observed in the larger $Nu_\theta$ at $\gamma =-2$ and the larger $Nu_T$ at $\gamma =2$. This can also be attributed to the differences between the Coriolis and buoyancy effects (3.2) and the specialized transfer characteristics of flow structures.

To further examine or demonstrate the validity of our conjectures for $Pr=1$, the mean velocity profiles $\langle u\rangle$ together with the normalized inertial-frame velocity profiles $\langle \theta \rangle$ at $Re=5000$, $Ri_\chi =0.16$ and $Pr=1$ are shown in figure 4. It can be seen in figure 4(a) that $\langle u\rangle$ strongly depends on $\gamma$. However, such dependence is mainly due to the velocity transformation relation between the inertial frame and the rotating frame. This is because $\langle \theta \rangle$ at different $\gamma$ almost coincide, as shown in figure 4(b), indicating the validity of the twin-force analogy. Furthermore, within $y\in [-0.3,0.3]$, there is $\langle \theta \rangle \approx 0$, which is equivalent to $\langle u\rangle \approx R_\varOmega y$ in the rotating frame. The local linear law of $\langle u\rangle$ is referred to as the zero mean absolute vorticity state (Hamba 2006; Grundestam, Wallin & Johansson 2008) in spanwise rotating plane Poiseuille turbulence. This behaviour can also be explained using the Lagrangian view (Zhang et al. 2019) as briefed in (3.1). A closer observation suggests the non-monotonicity of $\langle \theta \rangle$ at $\gamma =\pm 2$. This is similar to the non-monotonicity of mean temperature profiles in sheared Rayleigh–Bénard convection (Blass et al. 2021).

Figure 4. Mean profiles at $Re=5000$, $Ri_\chi =0.16$ and $Pr=1$ of (a) streamwise velocity $u$ and (b) normalized inertial-frame streamwise velocity $\theta =({R_\varOmega }y-u)/(1-{R_\varOmega })$.

Figure 5(a), demonstrating that the mean temperature profiles at $Re=5000$, $Ri_\chi =0.16$ and $Pr=1$ are almost invariant with $\gamma$, also supports the twin-force analogy. To examine the inertial-frame Reynolds analogy, we can examine the accuracy of estimating $\langle u\rangle$ at different $\gamma$ only with the $\langle T\rangle$ at $\gamma =+1$. Under the assumption that $\langle \theta \rangle \approx \langle T\rangle$, the estimation formula of $\langle u\rangle$ is $R_\varOmega y-(1-R_\varOmega )\langle T|_{\gamma =1}\rangle$, where $\langle T|_{\gamma =1}\rangle$ denotes the $\langle T\rangle$ in sheared Rayleigh–Bénard system ($\gamma =+1$) at the same $Re$ and $Ri_\chi$. As shown in figure 5(b), which depicts $\langle u\rangle$ and the corresponding estimations based on $\langle T|_{\gamma =1}\rangle$, the accuracy of the inertial-frame Reynolds analogy is satisfactory. In addition, figure 5(b) also suggests that the inertial-frame Reynolds analogy and the twin-force analogy can help to predict temperature or velocity profiles in complex rotating stratified systems with experimental results in less complex systems.

Figure 5. Mean profiles at $Re=5000$, $Ri_\chi =0.16$ and $Pr=1$ of (a) temperature $T$ and (b) velocity $u$, together with the estimations obtained from the $\langle T\rangle$ in sheared Rayleigh–Bénard convection ($\gamma =+1$).

Flow structures at $Pr=1$, $Ri_\chi =0.16$ and $\gamma =\pm 1$ are visualized in figure 6 with instantaneous contours of $\chi$ in the $y=0$ plane. Notably, the rotating plane Couette flow ($\gamma =-1$) and sheared Rayleigh–Bénard convection ($\gamma =+1$) have not been simultaneously visualized in prior studies. The observed large-scale streak-like structures, known as plume currents (Zhang et al. 2022), consist of plumes driven by either stratification or rotation, and drive the large-scale streamwise rolls. A striking similarity emerges when comparing the pure rotating and pure stratified systems at $Re=5000$. Figure 6(a) shows that there can be five pairs ($0< x<7$) or six pairs ($10< x<25$) of plume currents in the purely rotating case, and figure 6(b) shows that there can be five pairs of plume currents in the purely stratified case, indicating a close resemblance between the rotation and stratification effect on large-scale flow structures. It is worth noting that in the current periodic spanwise domain, the number of plume currents may be influenced by initial conditions (Huisman et al. 2014; Huang et al. 2019, 2020) or could change after extremely long simulation time (Zhang et al. 2022). However, usually, the sensitivity to initial condition only allows approximately a relative uncertainty of $\pm 1$ pairs of plume currents. Therefore, the large-scale patterns of the rotating plane Couette and sheared Rayleigh–Bénard systems at $Re=5000$ and $Pr=1$ would still be very similar even with possible variations depending on initial conditions. Difference in small-scale fluctuations can be inferred by more detailed observation on figure 6(a,b): plume currents induced by rotation are relatively narrower and straighter, while those induced by stratification are more chaotic. This can be attributed to the different expressions shown by (3.2) of the Coriolis and buoyancy effects on vorticity. Only the spanwise component of $\boldsymbol {k}$ appears in the Coriolis term, indicating that the self-sustaining process of rotation-induced structures mainly involves spanwise variations. In contrast, both $k_x$ and $k_z$ appear in the buoyancy term, indicating that the corresponding prevalent flow structures have larger degrees of freedom.

Figure 6. Instantaneous contours of $\chi$ in the $y=0$ plane at $Pr=1$ and $Ri_\chi =0.16$: (a) $Re=5000,\gamma =-1$; (b) $Re=5000,\gamma =+1$; (c) $Re=10\,000,\gamma =-1$; (d) $Re=10\,000,\gamma =+1$.

The changes of rotating plane Couette and sheared Rayleigh–Bénard systems under the increase of $Re$ are very different. Figure 6(c) shows that there are five pairs of plume currents in the purely rotating case at $Re=10\,000$, which is similar to the result at $Re=5000$, except that plume currents become more chaotic and fragmented. In contrast, as shown in figure 6(d), the purely stratified case at $Re=10\,000$ exhibits large streamwise variations of the spanwise distribution of plume currents. The spanwise distance between neighbouring plume currents varies between approximately $0.7$ and $3$. The primary reason is that larger $Re$ strongly activates the $k_x$ modes, and the distribution of flow structures tends to be more horizontally isotropic, under much weaker constraint on spanwise distance.

In contrast, the resemblance between Taylor–Couette turbulence and Rayleigh–Bénard convection is significantly weaker in terms of flow structures, even when carefully adjusting the parameters to yield similar Nusselt numbers (Brauckmann et al. 2017). To elaborate, while the governing equations remain identical in the context of traditional and sheared Rayleigh–Bénard convection, it is only the latter, characterized by wall shear, that engenders the elongated large-scale structures reminiscent of those in Taylor–Couette or rotating plane Couette turbulence. This delineates a pivotal insight: beyond the mathematical affinities elucidated in § 2.2, the consistency of symmetry and wall shear crucially contributes to the striking similarity observed among diverse rotating stratified wall turbulence. These findings provide compelling evidence for a much stronger connection between rotation-driven and stratification-driven dynamics when both are put in the background of wall turbulence.

Figure 7 shows the Nusselt numbers at $Re=5000$, $Ri_\chi =0.16$, and different values of $\gamma$ and $Pr\neq 1$. It can be seen that the behaviour of the heat, momentum and overall Nusselt numbers becomes more intricate as the Prandtl number ${Pr}$ varies. As shown in figure 7(a), for ${Pr}=0.25$, the heat Nusselt number is always smaller than the momentum Nusselt number, indicating that the thermal boundary layer is thicker than the momentum boundary layer in the inertial frame. This suggests that stratification has a globally larger influence than rotation in situations where ${Pr}\ll 1$. As the strength of unstable stratification increases with increasing $\gamma$, the overall enhancement of turbulence by rotation and stratification also increases, leading to an increase in both ${Nu}_T$ and ${Nu}_\theta$. At $\gamma =-2$, despite unstable rotation having a characteristic strength three times that of stable stratification, the unstable momentum boundary layer is embedded in the stable thermal boundary layer. This leads to partial laminarization and a significant decrease in both heat and momentum Nusselt numbers.

Figure 7. Heat Nusselt number ${Nu}_T$, momentum Nusselt number ${Nu}_\theta$ and overall Nusselt number ${Nu}_\chi$ as functions of the relative stratification-rotation difference $\gamma$ for plane Couette flow at $Re=5000$, $Ri_\chi =0.16$, and (a) $Pr=0.25$ and (b) $Pr=4$. The red and blue lines denote the heat and momentum Nusselt numbers, respectively, at the condition of ${Ri}_T={Ri}_\theta =0$.

The results at ${Pr}=4$ shown in figure 7(b) exhibit a trend that is exactly opposite to that of the ${Pr}=0.25$ cases. In this scenario, the momentum boundary layer is thicker than the thermal boundary layer, leading to the dominance of the rotation effect, and causing both ${Nu}_T$ and ${Nu}_\theta$ to increase as $\gamma$ decreases (increasing strength of unstable rotation). Notably, at $\gamma =2$, there is even a complete laminarization observed.

The present results perfectly demonstrated the appropriateness of our definition of $Ri_T$ in § 2.3. It has already been found that the twin-force analogy is valid at $Pr=1$, and it is obvious that in purely rotating cases ($\gamma =-1$), the $Nu_\chi =Nu_\theta$ is independent to $Pr$. As shown in table 1, in purely stratified cases ($\gamma =+1$), the $Nu_\chi =Nu_T$ is insensitive to $Pr$, which aligns with the intended purpose of the piecewise definition of $Ri_\chi$. Consequently, there are six cases at $Re=5000$, $Ri_\chi =0.16$ and $\gamma =\pm 1$ that have very similar $Nu_\chi$, which strongly supports the twin-force analogy.

While heat and momentum transport exhibit significant changes with $\gamma$ for ${Pr}\neq 1$, the overall Nusselt number ${Nu}_\chi$ at $Re=5000$ and ${Ri}_\chi =0.16$ shows weak dependence on ${Pr}$ and $\gamma$ for the cases that are not laminarized ($13$ out of $15$ cases at three $Pr$). This observation provides compelling evidence for the partial validity of the twin-force analogy across all values of $Pr$: $Nu_\chi$ is mainly determined by $Re$ and $Ri_\chi$, regardless of specific (stable or unstable) contributions from the rotation and stratification effect. In other words, rotation and stratification can serve as approximate substitutes for each other. Although the inertial-frame Reynolds analogy is generally invalid when ${Pr}\neq 1$, the transport behaviours of the systems can still be interpreted as those controlled by two buoyant scalars with distinct Prandtl or Schmidt numbers (Turner 1979; Yang, Verzicco & Lohse 2016; Garaud 2018).

The present results also indicate the similarity between Taylor–Couette flow and sheared Rayleigh–Bénard convection. We already found that when $Re$ is fixed, rotating plane Couette flow at a rotation number $0< R_\varOmega <0.5$ is very similar to sheared Rayleigh–Bénard convection at $Pr=1$ and $Ri_T$ taking the value of $R_\varOmega (1-R_\varOmega )$. For the Taylor–Couette system, it is reasonable to choose a rotating frame with angular velocity being the averaged value of the inner and outer cylinder, and define a $R_\varOmega$ using this angular velocity (Dubrulle et al. 2005; Brauckmann et al. 2016). Furthermore, Dubrulle et al. (2005) demonstrated that Taylor–Couette and plane Couette systems, when at the same $Re$ and $R_\varOmega$, exhibit significant similarities, especially when $\eta >0.71$. For classical Taylor–Couette systems with fixed outer cylinder, the definition of rotation number becomes $R_\varOmega =1-\eta$. Therefore, it is reasonable to anticipate that a Taylor–Couette system with radius ratio $\eta >1/2$ and fixed outer cylinder exhibits strong similarity to sheared Rayleigh–Bénard convection at $Ri_T$ being $R_\varOmega (1-R_\varOmega )=(1-\eta )[1-(1-\eta )]=\eta (1-\eta )$.

4. Conclusion

Our study has investigated the effects of rotation (Coriolis force) and stratification (buoyancy force) on plane Couette turbulence both separately and in combination. Previous and present simulation results indicate the validity of the twin-force analogy signifying that the Coriolis and buoyancy forces are ‘twin forces’ whose effects can be unified. Specifically, in turbulent cases at fixed $Re$ and $Pr$, the overall Nusselt number $Nu_\chi$ is primarily determined by the total strength of rotation and stratification characterized by the overall Richardson number $Ri_\chi$, which can be achieved by considerably arbitrary combinations of stratification and rotation. In the special case of $Pr=1$, large-scale flow structures driven by the buoyancy force are remarkably similar to those driven by the Coriolis force. In addition, the inertial-frame Reynolds analogy, standing for the approximate coincidence of heat and inertial-frame momentum transfer at $Pr=1$, is also valid. Building on these discoveries, we further conjecture that the ultimate Taylor–Couette turbulence with radius ratio $\eta >1/2$ and a fixed outer cylinder is nearly equivalent to high-Reynolds-number sheared Rayleigh–Bénard convection at $Pr=1$ and $Ri_T$ being $\eta (1-\eta )$, rather than the classical Rayleigh–Bénard convection.