Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-06T22:28:49.144Z Has data issue: false hasContentIssue false
  • English
  • Français

The turbulent wall plume from a vertically distributed source of buoyancy

Published online by Cambridge University Press:  15 December 2015

Craig D. McConnochie  and
Ross C. Kerr
Craig D. McConnochie*
Affiliation:
Research School of Earth Sciences, The Australian National University, Canberra, ACT 2601, Australia
Ross C. Kerr
Affiliation:
Research School of Earth Sciences, The Australian National University, Canberra, ACT 2601, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

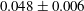We experimentally investigate the turbulent wall plume that forms next to a uniformly distributed source of buoyancy. Our experimental results are compared with the theoretical model and experiments of Cooper & Hunt (J. Fluid Mech., vol. 646, 2010, pp. 39–58). Our experiments give a top-hat entrainment coefficient of $0.048\pm 0.006$. We measure a maximum vertical plume velocity that follows the scaling predicted by Cooper & Hunt but is significantly smaller. Our measurements allow us to construct a turbulent plume model that predicts all plume properties at any height. We use this plume model to calculate plume widths, velocities and Reynolds numbers for typical dissolving icebergs and ice fronts and for a typical room with a heated or cooled vertical surface.

JFM classification

Convection: Convection in cavities Convection: Plumes/thermals Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 787 , 25 January 2016 , pp. 237 - 253
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baines, P. G. 2002 Two-dimensional plumes in stratified environments. J. Fluid Mech. 471, 315–337.Google Scholar
Baines, W. D. & Turner, J. S. 1969 Turbulent buoyant convection from a source in a confined region. J. Fluid Mech. 37, 51–80.Google Scholar
Budd, W. F., Jacka, T. H. & Morgan, V. I. 1980 Antarctic iceberg melt rates derived from size distributions and movement rates. Ann. Glaciol. 1, 103–112.CrossRefGoogle Scholar
Cheesewright, R. 1968 Turbulent natural convection from a vertical plane surface. Trans. ASME J. Heat Transfer 90, 1–6.CrossRefGoogle Scholar
Chen, Z. D., Li, Y. & Mahoney, J. 2001 Natural ventilation in an enclosure induced by a heat source distributed uniformly over a vertical wall. Build. Environ. 36, 493–501.Google Scholar
Cooper, P. & Hunt, G. R. 2010 The ventilated filling box containing a vertically distributed source of buoyancy. J. Fluid Mech. 646, 39–58.Google Scholar
Crone, T. J., McDuff, R. E. & Wilcock, W. S. D. 2008 Optical plume velocimetry: a new flow measurement technique for use in seafloor hydrothermal systems. Exp. Fluids 45, 899–915.Google Scholar
Dowdeswell, J. A. & Bamber, J. L. 2007 Keel depths of modern Antarctic icebergs and implications for sea-floor scouring in the geological record. Mar. Geol. 243, 120–131.Google Scholar
Gladstone, C. & Woods, A. W. 2014 Detrainment from a turbulent plume produced by a vertical line source of buoyancy in a confined, ventilated space. J. Fluid Mech. 742, 35–49.Google Scholar
Holman, J. P. 2010 Heat Transfer, 10th edn. McGraw-Hill.Google Scholar
Huppert, H. E. & Josberger, E. G. 1980 The melting of ice in cold stratified water. J. Phys. Oceanogr. 10 (6), 953–960.Google Scholar
Huppert, H. E. & Turner, J. S. 1980 Ice blocks melting into a salinity gradient. J. Fluid Mech. 100 (2), 367–384.Google Scholar
Jonassen, D. R., Settles, G. S. & Tronosky, M. D. 2006 Schlieren ‘PIV’ for turbulent flows. Opt. Lasers Engng. 44, 190–207.Google Scholar
Kerr, R. C. & McConnochie, C. D. 2015 Dissolution of a vertical solid surface by turbulent compositional convection. J. Fluid Mech. 765, 211–228.Google Scholar
Linden, P. F., Lane-Serff, G. F. & Smeed, D. A. 1990 Emptying filling boxes: the fluid mechanics of natural ventilation. J. Fluid Mech. 212, 309–335.Google Scholar
Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. 234, 1–23.Google Scholar
Nokes, R.2014 Streams, version 2.03: System theory and design. Department of Civil and Natural Resources Engineering, University of Canterbury, New Zealand.Google Scholar
Vliet, G. C. & Liu, C. K. 1969 An experimental study of turbulent natural convection boundary layers. Trans. ASME J. Heat Transfer 91, 517–531.CrossRefGoogle Scholar
Wells, A. J. & Worster, M. G. 2008 A geophysical-scale model of vertical natural convection boundary layers. J. Fluid Mech. 609, 111–137.Google Scholar