Article contents
The turbulent wake of a towed grid in a stratified fluid
Published online by Cambridge University Press: 19 June 2015
Abstract
In a stable background density gradient, initially turbulent flows eventually evolve into a state dominated by low-Froude-number dynamics and frequently also contain persistent pattern information. Much empirical evidence has been gathered on these latter stages, but less on how they first got that way, and how information on the turbulence generator may potentially be encoded into the flow in a robust and long-lasting fashion. Here an experiment is described that examines the initial stages of evolution in the vertical plane of a turbulent grid-generated wake in a stratified ambient. Refractive-index-matched fluids allow optically based measurement of early (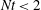 $Nt<2$) stages of the flow, even when there are strong variations in the local density gradient field. Suitably averaged flow measures show the interplay between internal wave motions and Kelvin–Helmholtz-generated vortical modes. The vertical shear is dominant at the wake edge, and the decay of horizontal vorticity is observed to be independent of
$Nt<2$) stages of the flow, even when there are strong variations in the local density gradient field. Suitably averaged flow measures show the interplay between internal wave motions and Kelvin–Helmholtz-generated vortical modes. The vertical shear is dominant at the wake edge, and the decay of horizontal vorticity is observed to be independent of  $\mathit{Fr}$. Stratified turbulence, originating from Kelvin–Helmholtz instabilities, develops up to non-dimensional time
$\mathit{Fr}$. Stratified turbulence, originating from Kelvin–Helmholtz instabilities, develops up to non-dimensional time 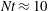 $Nt\approx 10$, and the scale separation between Ozmidov and Kolmogorov scales is independent of
$Nt\approx 10$, and the scale separation between Ozmidov and Kolmogorov scales is independent of 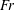 $\mathit{Fr}$ at higher
$\mathit{Fr}$ at higher 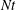 $Nt$. The detailed measurements in the near wake, with independent variation of both Reynolds and Froude numbers, while limited to one particular case, are sufficient to show that the initial turbulence in a stratified fluid is neither three-dimensional nor universal. The search for appropriately generalizable initial conditions may be more involved than hoped for.
$Nt$. The detailed measurements in the near wake, with independent variation of both Reynolds and Froude numbers, while limited to one particular case, are sufficient to show that the initial turbulence in a stratified fluid is neither three-dimensional nor universal. The search for appropriately generalizable initial conditions may be more involved than hoped for.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 15
- Cited by



