Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-12-01T00:11:17.672Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent two-phase plumes with bubble-size reduction owing to dissolution or chemical reaction

Published online by Cambridge University Press:  25 January 2013

Mariana G. Domingos  and
Silvana S. S. Cardoso
Mariana G. Domingos
Affiliation:
Department of Chemical Engineering and Biotechnology, University of Cambridge, Pembroke Street, Cambridge CB2 3RA, UK
Silvana S. S. Cardoso*
Affiliation:
Department of Chemical Engineering and Biotechnology, University of Cambridge, Pembroke Street, Cambridge CB2 3RA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Turbulent two-phase plumes consisting of a continuous phase of entrained fluid and a dispersed phase, in the form of buoyant droplets/bubbles, are investigated. Chemical reaction or dissolution causes both a decrease in the size of the droplets/bubbles and a change in the buoyancy of the plume. The behaviours of such a plume in environments with uniform and stratified density are considered. We show that the dynamics of the plume are determined by two dimensionless groups: 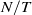$N/ T$ and 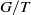$G/ T$. Here, 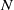$N$ is the buoyancy frequency of the environment, 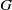$G$ measures the ability of the reaction to change buoyancy and 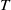$T$ reflects the effect of reaction on the size of the droplets/bubbles. We identify four regimes of behaviour of a plume in a stratified environment depending on whether the dominant effect on buoyancy arises from reaction or stratification, and on the occurrence of either multiple or single zero-buoyancy levels. For a uniform environment, perturbation solutions for the fluxes of volume, momentum, buoyancy and chemical species as a function of ascent distance are obtained. We apply our findings to understand the dynamics of both of the cases of a release of methane and a release of carbon dioxide in the ocean. For a methane release in the Gulf of Mexico, the motion of the plume is shown to be controlled by external density stratification for a bubble diameter of methane above 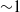${\sim }1$–2 mm. In the case of a carbon dioxide release in the Norwegian Sea, dissolution determines the motion of the plume when the bubble diameter is smaller than 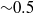${\sim }0. 5$–3.5 cm. In both scenarios, the plume releases seawater enriched with the chemical at multiple levels.

JFM classification

Convection: Plumes/thermals Turbulent Flows: Turbulent convection Reacting Flows: Turbulent reacting flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 716 , 10 February 2013 , pp. 120 - 136
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asaeda, T. & Imberger, J. 1993 Structure of bubble plumes in linearly stratified environments. J. Fluid Mech. Digital Arch. 249 (1), 35–57.CrossRefGoogle Scholar
Brewer, P., Peltzer, E. & Friedrich, G. G. R. 2002 Experimental determination of the fate of rising ${\mathrm{CO} }_{2} $ droplets in seawater. Environ. Sci. Technol. 36, 5441–5446.CrossRefGoogle Scholar
Camilli, R., Reddy, C. M., Yoerger, D. R., Van Mooy, B. A. S., Jakuba, M. V., Kinsey, J. C., Mc Intyre, C. P., Sylva, S. P. & Maloney, J. V. 2010 Tracking hydrocarbon plume transport and biodegradation at deepwater horizon. Science 330 (6001), 201–204.Google Scholar
Campbell, A. N. & Cardoso, S. S. S. 2010 Turbulent plumes with internal generation of buoyancy by chemical reaction. J. Fluid Mech. 655, 122–151.CrossRefGoogle Scholar
Cardoso, S. S. S. & McHugh, S. T. 2010 Turbulent plumes with heterogeneous chemical reaction on the surface of small buoyant droplets. J. Fluid Mech. 642 (-1), 49–77.CrossRefGoogle Scholar
Chen, M. H. & Cardoso, S. S. S. 2000 The mixing of liquids by a plume of low-Reynolds number bubbles. Chem. Engng Sci. 55 (14), 2585–2594.CrossRefGoogle Scholar
Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles, Drops and Particles. Academic.Google Scholar
Conroy, D. T. & Smith, S. G. L. 2008 Endothermic and exothermic chemically reacting plumes. J. Fluid Mech. 612 (-1), 291–310.CrossRefGoogle Scholar
Duan, Z. & Mao, S. 2006 A thermodynamic model for calculating methane solubility, density and gas phase composition of methane-bearing aqueous fluids from 273 to 523 K and from 1 to 2000 bar. Geochim. Cosmochim. Acta 70 (13), 3369–3386.CrossRefGoogle Scholar
Duan, Z., Sun, R., Zhu, C. & Chou, I. M. 2006 An improved model for the calculation of ${\mathrm{CO} }_{2} $ solubility in aqueous solutions containing ${\mathrm{Na} }^{+ } $ , ${\mathrm{K} }^{+ } $ , ${\mathrm{Ca} }^{2+ } $ , ${\mathrm{Mg} }^{2+ } $ , ${\mathrm{Cl} }^{- } $ , and ${ \mathrm{SO} }_{4}^{2- } $ . Mar. Chem. 98 (2–4), 131–139.Google Scholar
Fogg, P. G. T. & Gerrard, W. 1991 Solubility of Gases and Liquids. John Wiley & Sons.Google Scholar
Hunt, G. R. & Kaye, N. G. 2001 Virtual origin correction for lazy turbulent plumes. J. Fluid Mech. 435 (-1), 377–396.Google Scholar
Hunt, G. R. & van den Bremer, T. S. 2011 Classical plume theory: 1937–2010 and beyond. IMA J. Appl. Math. 76 (3), 424–448.Google Scholar
Kaye, N. B. & Scase, M. M. 2011 Straight-sided solutions to classical and modified plume flux equations. J. Fluid Mech. 680, 564–573.Google Scholar
Koh, C. A., Westacott, R. E., Zhang, W., Hirachand, K., Creek, J. L. & Soper, A. K. 2002 Mechanisms of gas hydrate formation and inhibition. Fluid Phase Equilib. 194–197, 143–151.Google Scholar
McHugh, S. T. & Cardoso, S. S. S. 2011 Turbulent entrainment into inert and reacting multiphase plumes. J. Fluid Mech. 682, 577–589.CrossRefGoogle Scholar
Metz, B., Davidson, O., de Coninck, H. C., Loos, M. & Meyer, L. Eds. 2005 IPCC Special Report on Carbon Dioxide Capture and Storage. Cambridge, UK, Working Group III of the Intergovernmental Panel for Climate Change.Google Scholar
Milgram, J. H. 1983 Mean flow in round bubble plumes. J. Fluid Mech. Digital Arch. 133 (-1), 345–376.Google Scholar
Millero, F. J. & Poisson, A. 1981 International one-atmosphere equation of state of seawater. Deep-Sea Res. Part A. Oceanogr. Res. Papers 28 (6), 625–629.CrossRefGoogle Scholar
Morton, B. R. 1959 Forced plumes. J. Fluid Mech. Digital Arch. 5 (01), 151–163.CrossRefGoogle Scholar
Morton, B. R. & Middleton, J. 1973 Scale diagrams for forced plumes. J. Fluid Mech. Digital Arch. 58 (01), 165–176.Google Scholar
Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. 234, 1–23.Google Scholar
Setzmann, U. & Wagner, W. 1991 A new equation of state and tables of thermodynamic properties for methane covering the range from the melting line to 625 K at pressures up to 1000 MPa. J. Phys. Chem. Ref. Data 20 (6), 1061–1151.Google Scholar
Socolofsky, S. A. & Adams, E. E. 2005 Role of slip velocity in the behavior of stratified multiphase plumes. J. Hydraul. Engng 131 (4), 273–282.Google Scholar
Song, Y., Chen, B., Nishio, M. & Akai, M. 2003 The study on density change of carbon dioxide seawater solution at high pressure and low temperature. Energy 30 (11–12), 2298–2307.Google Scholar
Woods, A. W. 2010 Turbulent plumes in nature. Annu. Rev. Fluid Mech. 42 (1), 391–412.Google Scholar
Zhang, Y. 2005 Fate of rising ${\mathrm{CO} }_{2} $ droplets in seawater. Environ. Sci. Technol. 39 (19), 7719–7724.Google Scholar