Article contents
Turbulent three-dimensional dielectric electrohydrodynamic convection between two plates
Published online by Cambridge University Press: 24 February 2012
Abstract
The fundamental mechanisms responsible for the creation of electrohydrodynamically driven roll structures in free electroconvection between two plates are analysed with reference to traditional Rayleigh–Bénard convection (RBC). Previously available knowledge limited to two dimensions is extended to three-dimensions, and a wide range of electric Reynolds numbers is analysed, extending into a fully inherently three-dimensional turbulent regime. Results reveal that structures appearing in three-dimensional electrohydrodynamics (EHD) are similar to those observed for RBC, and while two-dimensional EHD results bear some similarities with the three-dimensional results there are distinct differences. Analysis of two-point correlations and integral length scales show that full three-dimensional electroconvection is more chaotic than in two dimensions and this is also noted by qualitatively observing the roll structures that arise for both low (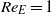 ) and high electric Reynolds numbers (up to
) and high electric Reynolds numbers (up to 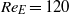 ). Furthermore, calculations of mean profiles and second-order moments along with energy budgets and spectra have examined the validity of neglecting the fluctuating electric field
). Furthermore, calculations of mean profiles and second-order moments along with energy budgets and spectra have examined the validity of neglecting the fluctuating electric field 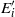 in the Reynolds-averaged EHD equations and provide insight into the generation and transport mechanisms of turbulent EHD. Spectral and spatial data clearly indicate how fluctuating energy is transferred from electrical to hydrodynamic forms, on moving through the domain away from the charging electrode. It is shown that
in the Reynolds-averaged EHD equations and provide insight into the generation and transport mechanisms of turbulent EHD. Spectral and spatial data clearly indicate how fluctuating energy is transferred from electrical to hydrodynamic forms, on moving through the domain away from the charging electrode. It is shown that  is not negligible close to the walls and terms acting as sources and sinks in the turbulent kinetic energy, turbulent scalar flux and turbulent scalar variance equations are examined. Profiles of hydrodynamic terms in the budgets resemble those in the literature for RBC; however there are terms specific to EHD that are significant, indicating that the transfer of energy in EHD is also attributed to further electrodynamic terms and a strong coupling exists between the charge flux and variance, due to the ionic drift term.
is not negligible close to the walls and terms acting as sources and sinks in the turbulent kinetic energy, turbulent scalar flux and turbulent scalar variance equations are examined. Profiles of hydrodynamic terms in the budgets resemble those in the literature for RBC; however there are terms specific to EHD that are significant, indicating that the transfer of energy in EHD is also attributed to further electrodynamic terms and a strong coupling exists between the charge flux and variance, due to the ionic drift term.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 37
- Cited by


