Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-29T04:35:27.569Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent mixing and entrainment in a stratified horizontal plane shear layer: joint velocity–temperature analysis of experimental data

Published online by Cambridge University Press:  10 October 2016

Johan Carlier  and
Kodjovi Sodjavi
Johan Carlier*
Affiliation:
Irstea, UR OPAALE, F-35044 Rennes CEDEX, France
Kodjovi Sodjavi
Affiliation:
Irstea, UR OPAALE, F-35044 Rennes CEDEX, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Buoyancy effects on the turbulent mixing and entrainment processes were analysed in the case of a stratified plane shear layer between two horizontal air flows in conditions leading to relatively low values of the flux Richardson number (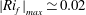$|Ri_{f}|_{max}\simeq 0.02$). Velocity and temperature measurements were made with a single $\times$-wire probe thermo-anemometry technique, using multi-overheat sequences to deliver simultaneous velocity–temperature data at high frequency. The spatial resolution was found to be fine enough, in relation to the dissipative scale and the thermal diffusive scale, to avoid false mixing enhancement in the analysis of the physical mechanisms through velocity–temperature coupling in statistical turbulence quantities. Probability density functions (PDFs) and joint probability density functions (JPDFs) were used to distinguish between the different mechanisms involved in turbulent mixing, namely entrainment, engulfing, nibbling and mixing, and point to the contribution of entrainment in the mixing process. When comparing an unstably stratified configuration to its stably stratified equivalent, no significant difference could be seen in the PDF and JPDF quantities, but a conditional analysis based on temperature thresholding enabled a separation between mixed fluid and two distinct sets of events associated with unmixed fluid entrained from the hot and cold sides of the mixing layer into the mixing layer. This separation allowed a direct calculation of the entrainment velocities on both sides of the mixing layer. A significant increase of the total entrainment could be seen in the case of unstably stratified configuration. The entrainment ratios were compared to their prediction by the Dimotakis model and both a rather good relevance of the model and some need for improvement were found from the comparison. It was hypothesised that the improvement should come from better taking into account the distinct contributions of nibbling and engulfing inside the process of entrainment and mixing.

JFM classification

Turbulent Flows: Shear layer turbulence Turbulent Flows: Stratified turbulence Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 806 , 10 November 2016 , pp. 542 - 579
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akula, B., Andrews, M. J. & Ranjan, D. 2013 Effect of shear on Rayleigh–Taylor mixing at small Atwood number. Phys. Rev. E 87, 033013.Google Scholar
Antonia, R. A. 1981 Conditional sampling in turbulence measurement. Annu. Rev. Fluid Mech. 13 (1), 131–156.Google Scholar
Batt, R. G. 1977 Turbulent mixing of passive and chemically reacting species in a low-speed shear layer. J. Fluid Mech. 82 (1), 53–95.Google Scholar
Bell, J. H. & Mehta, R. D. 1990 Development of a two-stream mixing layer from tripped and untripped boundary layers. AIAA J. 28 (12), 2034–2042.CrossRefGoogle Scholar
Bernal, L. P. & Roshko, A. 1986 Streamwise vortex structure in plane mixing layers. J. Fluid Mech. 170, 499–525.CrossRefGoogle Scholar
Bradshaw, P. 1966 The effect of initial conditions on development of free shear layer. J. Fluid Mech. 27, 225–236.CrossRefGoogle Scholar
Broadwell, J. E. & Breidenthal, R. E. 1982 A simple model of mixing and chemical reaction in a turbulent shear layer. J. Fluid Mech. 125, 397–410.CrossRefGoogle Scholar
Broadwell, J. E. & Mungal, M. G. 1991 Large-scale structures and molecular mixing. Phys. Fluids 3 (5), 1193–1206.Google Scholar
Brown, G. L. 1974 The entrainment and large structure in turbulent mixing layers. In 5th Australasian Conference on Hydraulics and Fluid Mechanics, pp. 352–359. University of Canterbury.Google Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64 (4), 775–816.Google Scholar
Buch, K. A. & Dahm, W. J. A. 1998 Experimental study of the fine-scale structure of conserved scalar mixing in turbulent shear flows. Part 2. Sc ≈ 1. J. Fluid Mech. 364, 1–29.CrossRefGoogle Scholar
Coles, D. 1981 Prospects for useful research on coherent structure in turbulent shear flow. Proc. Indian Acad. Sci. C 4 (2), 111–127.CrossRefGoogle Scholar
Corcos, G. M. & Lin, S. J. 1984 The mixing layer: deterministic models of a turbulent flow. Part 2. The origin of the three-dimensional motion. J. Fluid Mech. 139, 67–95.Google Scholar
Corrsin, S. 1947 Extended applications of hot-wire anemometer. Rev. Sci. Instrum. 18 (7), 469–471.Google Scholar
Corrsin, S. & Kistler, A. L.1954, Free-stream boundaries of turbulent flows. Tech. Rep. NACA.Google Scholar
Cortesi, A. B., Smith, B. L., Sigg, B. & Banerjee, S. 2001 Numerical investigation of the scalar probability density function distribution in neutral and stably stratified mixing layers. Phys. Fluids 13 (4), 927–950.Google Scholar
Dimotakis, P. E. 1986 Two-dimensional shear-layer entrainment. AIAA J. 24 (11), 1791–1796.CrossRefGoogle Scholar
Dimotakis, P. E. 1989 Turbulent shear layer mixing with fast chemical reactions. In Turbulent Reactive Flows, pp. 417–485. Springer.Google Scholar
Dimotakis, P. E. 1991 Turbulent free shear layer mixing and combustion. High Speed Flight Propul. Syst. 137, 265–340.Google Scholar
D’Ovidio, A. & Coats, C. M. 2013 Organized large structure in the post-transition mixing layer. Part 1. Experimental evidence. J. Fluid Mech. 737, 466–498.CrossRefGoogle Scholar
Eckart, C. 1948 An analysis of the stirring and mixing processes in incompressible fluids. J. Mar. Res. 7, 265–275.Google Scholar
Fiedler, H. E. 1974 Transport of heat across a plane turbulent mixing layer. Adv. Geophys. 18, 93–109.CrossRefGoogle Scholar
Fontane, J. & Joly, L. 2008 The stability of the variable-density Kelvin–Helmholtz billow. J. Fluid Mech. 612, 237–260.CrossRefGoogle Scholar
Gampert, M., Boschung, J., Hennig, F., Gauding, M. & Peters, N. 2014 The vorticity versus the scalar criterion for the detection of the turbulent/non-turbulent interface. J. Fluid Mech. 750, 578–596.Google Scholar
Hernan, M. A. & Jimenez, J. 1982 Computer analysis of a high-speed film of the plane turbulent mixing layer. J. Fluid Mech. 119, 323–345.Google Scholar
Ho, C.-M. & Huang, L.-S. 1982 Subharmonics and vortex merging in mixing layers. J. Fluid Mech. 119, 443–473.CrossRefGoogle Scholar
Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10, 509–512.Google Scholar
Huang, L.-S. & Ho, C.-M. 1990 Small-scale transition in a plane mixing layer. J. Fluid Mech. 210, 475–500.Google Scholar
Jacobitz, F. G., Sarkar, S. & Van Atta, C. W. 1997 Direct numerical simulations of the turbulence evolution in a uniformly sheared and stably stratified flow. J. Fluid Mech. 342, 231–261.CrossRefGoogle Scholar
Karasso, P. S. & Mungal, M. G. 1996 Scalar mixing and reaction in plane liquid shear layers. J. Fluid Mech. 323, 23–63.Google Scholar
Klaassen, G. P. & Peltier, W. R. 1991 The influence of stratification on secondary instability in free shear layers. J. Fluid Mech. 227, 71–106.CrossRefGoogle Scholar
Konrad, J. H.1977 An experimental investigation of mixing in two-dimensional turbulent shear flows with application to diffusion-limited chemical reactions. PhD thesis, California Institute of Technology.Google Scholar
Koochesfahani, M. M., Cohn, R. & MacKinnon, C. 2000 Simultaneous whole-field measurements of velocity and concentration fields using a combination of MTV and LIF. Meas. Sci. Technol. 11 (9), 1289–1300.Google Scholar
Koochesfahani, M. M. & Dimotakis, P. E. 1986 Mixing and chemical reactions in a turbulent liquid mixing layer. J. Fluid Mech. 170, 83–112.CrossRefGoogle Scholar
Koochesfahani, M. M., Dimotakis, P. E., Catherasoo, C. J., Gharib, M. & Lang, D. B. 1979 Two-point LDV measurements in a plane mixing layer. AIAA J. 17 (12), 1347–1351.CrossRefGoogle Scholar
Lasheras, J. C., Cho, J. S. & Maxworthy, T. 1986 On the origin and evolution of streamwise vortical structures in a plane, free shear layer. J. Fluid Mech. 172, 231–258.Google Scholar
Lasheras, J. C. & Choi, H. 1988 Three-dimensional instability of a plane free shear layer: an experimental study of the formation and evolution of streamwise vortices. J. Fluid Mech. 189, 53–86.Google Scholar
Li, C.-T., Chang, K.-C. & Wang, M.-R. 2010a Experimental study on evolution of joint velocity PDF in planar mixing layer. Exp. Therm. Fluid Sci. 34 (8), 1122–1132.Google Scholar
Li, N., Balaras, E. & Wallace, J. M. 2010b Passive scalar transport in a turbulent mixing layer. Flow Turbul. Combust. 85 (1), 1–24.CrossRefGoogle Scholar
Lienhard, J. H.1988 The decay of turbulence in thermally stratified flow. PhD thesis, University of California, San Diego.Google Scholar
Lienhard, J. H. & Van Atta, C. W. 1990 The decay of turbulence in thermally stratified flow. J. Fluid Mech. 210, 57–112.Google Scholar
Masutani, S. M. & Bowman, C. T. 1986 The structure of a chemically reacting plane mixing layer. J. Fluid Mech. 172, 93–126.CrossRefGoogle Scholar
Mathew, J. & Basu, A. J. 2002 Some characteristics of entrainment at a cylindrical turbulence boundary. Phys. Fluids 14 (7), 2065–2072.Google Scholar
Meyer, T. R., Dutton, J. C. & Lucht, R. P. 2006 Coherent structures and turbulent molecular mixing in gaseous planar shear layers. J. Fluid Mech. 558, 179–205.Google Scholar
Michalke, A. 1965 On spatially growing disturbances in an inviscid shear layer. J. Fluid Mech. 23, 521–544.Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.Google Scholar
Monkewitz, P. A. & Huerre, P. 1982 Influence of the velocity ratio on the spatial instability of mixing layers. Phys. Fluids 25 (7), 1137–1143.Google Scholar
Mungal, M. G. & Dimotakis, P. E. 1984 Mixing and combustion with low heat release in a turbulent shear layer. J. Fluid Mech. 148, 349–382.Google Scholar
Nagata, K. & Komori, S. 2000 The effects of unstable stratification and mean shear on the chemical reaction in grid turbulence. J. Fluid Mech. 408, 39–52.CrossRefGoogle Scholar
Ndoye, M., Delville, J., Heitz, D. & Arroyo, G. 2010 Parameterizable constant temperature anemometer: a new method for the analysis of velocity-temperature coupling in turbulent heat transfer. Meas. Sci. Technol. 21 (7), 075401.Google Scholar
Philip, J., Meneveau, C., de Silva, C. M. & Marusic, I. 2014 Multiscale analysis of fluxes at the turbulent/non-turbulent interface in high Reynolds number boundary layers. Phys. Fluids 26 (1), 015105.Google Scholar
Piccirillo, P. & Van Atta, C. W. 1997 The evolution of a uniformly sheared thermally stratified turbulent flow. J. Fluid Mech. 334, 61–86.Google Scholar
Pickett, L. M. & Ghandhi, J. B. 2001 Passive scalar measurements in a planar mixing layer by PLIF of acetone. Exp. Fluids 31, 309–318.Google Scholar
Pickett, L. M. & Ghandhi, J. B. 2002 Passive scalar mixing in a planar shear layer with laminar and turbulent inlet conditions. Phys. Fluids 14, 985–998.CrossRefGoogle Scholar
Pierrehumbert, R. T. & Widnall, S. E. 1982 The two- and three-dimensional instabilities of a spatially periodic shear layer. J. Fluid Mech. 114, 59–82.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Prasad, R. R. & Sreenivasan, K. R. 1989 Scalar interfaces in digital images of turbulent flows. Exp. Fluids 7 (4), 259–264.Google Scholar
Reinaud, J., Joly, L. & Chassaing, P. 2000 The baroclinic secondary instability of the two-dimensional shear layer. Phys. Fluids 12 (10), 2489–2505.Google Scholar
Sandham, N. D., Mungal, M. G., Broadwell, J. E. & Reynolds, W. C. 1988 Scalar entrainment in the mixing layer. In Proceedings of the CTR Summer Program, pp. 69–76. Stanford University.Google Scholar
Schowalter, D. G., Van Atta, C. W. & Lasheras, J. C. 1994 A study of streamwise vortex structure in a stratified shear layer. J. Fluid Mech. 281, 247–291.Google Scholar
da Silva, C. B., Hunt, J. C. R., Eames, I. & Westerweel, J. 2014 Interfacial layers between regions of different turbulence intensity. Annu. Rev. Fluid Mech. 46 (1), 567–590.Google Scholar
Smyth, W. D. 2003 Secondary Kelvin–Helmholtz instability in weakly stratified shear flow. J. Fluid Mech. 497, 67–98.Google Scholar
Sodjavi, K. & Carlier, J. 2013 Experimental study of thermal mixing layer using variable temperature hot-wire anemometry. Exp. Fluids 54 (10), 1–19.Google Scholar
Soteriou, M. C. & Ghoniem, A. F. 1995 Effects of the free-stream density ratio on free and forced spatially developing shear layers. Phys. Fluids 7 (8), 2036–2051.Google Scholar
Spencer, B. W. & Jones, B. G. 1971 Statistical investigation of pressure and velocity fields in the turbulent two-stream mixing layer. In AIAA 4th Fluid and Plasma Dynamical Conference, pp. 71–613. AIAA.Google Scholar
Staquet, C. 1995 Two-dimensional secondary instabilities in a strongly stratified shear layer. J. Fluid Mech. 296, 73–126.CrossRefGoogle Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT.Google Scholar
Townsend, A. A. 1966 The mechanism of entrainment in free turbulent flows. J. Fluid Mech. 26, 689–715.Google Scholar
Townsend, A. A. 1976 Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vinçont, J.-Y., Simoëns, S., Ayrault, M. & Wallace, J. M. 2000 Passive scalar dispersion in a turbulent boundary layer from a line source at the wall and downstream of an obstacle. J. Fluid Mech. 424, 127–167.Google Scholar
Wallace, J. M., Eckelmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54, 39–48.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. & Hunt, J. 2005 Mechanics of the turbulent-nonturbulent interface of a jet. Phys. Rev. Lett. 95 (17), 174501.Google Scholar
Willmarth, W. W. & Lu, S. S. 1972 Structure of the Reynolds stress near the wall. J. Fluid Mech. 55, 65–92.Google Scholar
Wiltse, J. M. & Glezer, A. 2004 Scalar mixing in a forced non-reactive plane shear layer using a thermal analogue to species concentration. J. Fluid Mech. 506, 369–406.Google Scholar
Winant, C. D. & Browand, F. K. 1974 Vortex pairing: the mechanism of turbulent mixing-layer growth at moderate Reynolds number. J. Fluid Mech. 63 (02), 237–255.CrossRefGoogle Scholar
Wygnanski, I. & Fiedler, H. E. 1970 the two-dimensionnal mixing region. J. Fluid Mech. 41, 327–361.Google Scholar
Yoon, K. & Warhaft, Z. 1990 The evolution of grid-generated turbulence under conditions of stable thermal stratification. J. Fluid Mech. 215, 601–638.Google Scholar
Zhou, X. Y. & Pereira, J. C. F. 2000 Large eddy simulation (2D) of a reacting plane mixing layer using filtered density function closure. Flow Turbul. Combust. 64 (4), 279–300.Google Scholar