Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T11:54:42.131Z Has data issue: false hasContentIssue false
  • English
  • Français

The turbulent kinetic energy budget in a bubble plume

Published online by Cambridge University Press:  01 March 2019

Chris C. K. Lai Open the ORCID record for Chris C. K. Lai [Opens in a new window]  and
Scott A. Socolofsky
Chris C. K. Lai*
Affiliation:
P-23, Physics Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA Zachry Department of Civil Engineering, Texas A&M University, College Station, TX 77843, USA
Scott A. Socolofsky
Affiliation:
Zachry Department of Civil Engineering, Texas A&M University, College Station, TX 77843, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

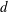We present the turbulent kinetic energy (t.k.e.) budget of a dilute bubble plume in its asymptotic state. The budget is derived from an experimental dataset of bubble plumes formed inside an unstratified water tank. The experiments cover both the adjustment phase and asymptotic state of the plume. The diameters $d$ of air bubbles are in the range 1–4 mm and the air void fraction 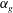$\unicode[STIX]{x1D6FC}_{g}$ is between 0.7 % and 1.8 %. We measured the three components of the instantaneous liquid velocity vector with a profiling acoustic Doppler velocimeter. From the experiments, we found the following inside the heterogeneous bubble core of the plume: (i) the probability density functions of the standardized liquid fluctuations are very similar to those of homogeneous bubble swarms rising with and without background liquid turbulence; (ii) the characteristic temporal frequency 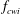$f_{cwi}$ at which bubbles inject t.k.e. into the liquid agrees with the prediction 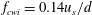$f_{cwi}=0.14u_{s}/d$ observed and theoretically derived for homogeneous bubble swarms (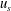$u_{s}$ is the bubble slip velocity); (iii) the liquid turbulence is anisotropic with the ratio of turbulence intensities between the vertical and horizontal components in the range 1.9–2.1; (iv) the t.k.e. production by air bubbles is much larger than that by liquid mean shear; and (v) an increasing fraction of the available work done by bubbles is deposited into liquid turbulence as one moves away from the plume centreline. Together with the existing knowledge of homogeneous bubble swarms, our results of the heterogeneous bubble plume support the view that millimetre-sized bubbles create specific patterns of liquid fluctuations that are insensitive to flow conditions and can therefore be possibly modelled by a universal form.

JFM classification

Wakes/Jets: Jets Turbulent Flows: Shear layer turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 865 , 25 April 2019 , pp. 993 - 1041
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Almeras, E., Mathai, V., Lohse, D. & Sun, C. 2017 Experimental investigation of the turbulence induced by a bubble swarm rising within incident turbulence. J. Fluid Mech. 825, 1091–1112.10.1017/jfm.2017.410Google Scholar
Asad, A., Kratzsch, C. & Schwarze, R. 2017 Influence of drag closures and inlet conditions on bubble dynamics and flow behavior inside a bubble column. Engng Appl. Comput. Fluid Mech. 11 (1), 127–141.Google Scholar
Bombardelli, F. A., Buscaglia, G. C., Rehmann, C. R., Rincon, L. E. & Garcia, M. H. 2007 Modeling and scaling of aeration bubble plumes: a two-phase flow analysis. J. Hydraul. Res. 45 (5), 617–630.10.1080/00221686.2007.9521798Google Scholar
Cea, L., Puertas, J. & Pena, L. 2007 Velocity measurements on highly turbulent free surface flow. Exp. Fluids 42, 333–348.10.1007/s00348-006-0237-3Google Scholar
Charonko, J. J. & Prestridge, K. 2017 Variable-density mixing in turbulent jets with coflow. J. Fluid Mech. 825, 921–997.10.1017/jfm.2017.379Google Scholar
Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles, Drops and Particles. Academic Press.Google Scholar
Craig, R., Loadman, C., Clement, B., Rusello, P. & Siegel, E. 2011 Characterization and testing of a new bistatic profiling acoustic Doppler velocimete: the Vectrino II. In IEES/OES Tenth Current, Waves, and Turbulence Measurement Workshop, Monterey, CA, pp. 246–252. IEEE, doi:10.1109/CWTM.2011.5759559.Google Scholar
Darisse, A., Lemay, J. & Benaissa, A. 2015 Budgets of turbulent kinetic energy, Reynolds stresses, variance of temperature fluctuations and turbulent heat fluxes in a round jet. J. Fluid Mech. 774, 95–142.10.1017/jfm.2015.245Google Scholar
Daubechies, I. 1990 The wavelet transform time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 36 (5), 961–1004.10.1109/18.57199Google Scholar
Deen, N. G., Solberg, T. & Hjertager, B. H. 2001 Large eddy simulation of the gas–liquid flow in a square cross-sectioned bubble column. Chem. Engng Sci. 56, 6341–6349.10.1016/S0009-2509(01)00249-4Google Scholar
Duncan, B. B., Seol, D.-G. & Socolofsky, S. A. 2009 Quantification of turbulence properties in bubble plumes using vortex identification methods. Phys. Fluids 21 (7), 075101.Google Scholar
Fannelop, T. K. & Sjoen, K. 1980 Hydrodynamics of underwater blowouts. In Proceedings AIAA 18th Aerospace Sci. Meeting, Pasadena, California. AIAA.Google Scholar
Farge, M. 1992 Wavelet transforms and their applications to turbulence. Annu. Rev. Fluid Mech. 24, 395–457.10.1146/annurev.fl.24.010192.002143Google Scholar
Fischer, H. B., List, E. J., Koh, R. C. Y., Brooks, N. H. & Imberger, J. 1979 Mixing in Inland and Coastal Waters. Academic Press.Google Scholar
Fraga, B. & Stoesser, T. 2016 Influence of bubble size, diffuser width, and flow rate on the integral behavior of bubble plumes. J. Geophys. Res. Oceans 121, 3887–3904.10.1002/2015JC011381Google Scholar
Fraga, B., Stoesser, T., Lai, C. C. K. & Socolofsky, S. A. 2016 An les-based Eulerian–Lagrangian approach to predict the dynamics of bubble plumes. Ocean Model. 97, 27–36.10.1016/j.ocemod.2015.11.005Google Scholar
Garcia, C. M., Cantero, M. I., Nino, Y. & Garcia, M. H. 2005 Turbulence measurements with acoustic Doppler velocimeters. J. Hydraul. Engng ASCE 131 (12), 1062–1073.10.1061/(ASCE)0733-9429(2005)131:12(1062)Google Scholar
George, W. K. & Hussein, H. 1991 Locally axisymmetric turbulence. J. Fluid Mech. 233, 1–23.10.1017/S0022112091000368Google Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2015 The energy cascade in near-field non-homogeneous non-isotropic turbulence. J. Fluid Mech. 771, 676–705.10.1017/jfm.2015.201Google Scholar
Goring, D. G. & Nikora, V. I. 2002 Despiking acoustic Doppler velocimeter data. J. Hydraul. Engng ASCE 128 (1), 117–126.10.1061/(ASCE)0733-9429(2002)128:1(117)Google Scholar
Heskestad, G. 1965 A generalized Taylor hypothesis with application for high Reynolds number turbulent flows. J. Appl. Mech. 32, 735–739.10.1115/1.3627310Google Scholar
Hosokawa, S. & Suzuki, T. 2012 Turbulence kinetic energy budget in bubbly flows in a vertical duct. Exp. Fluids 52, 719–728.10.1007/s00348-011-1109-zGoogle Scholar
Hurther, D. & Lemmin, U. 2001 A correction method for turbulence measurements with a 3D acoustic Doppler velocity meter. J. Atmos. Ocean. Technol. 18, 446–458.10.1175/1520-0426(2001)018<0446:ACMFTM>2.0.CO;22.0.CO;2>Google Scholar
Hussein, H. J., Capp, S. & George, W. K. 1994 Velocity measurements in a high-Reynolds number, momentum-conserving, axisymmetric, turbulent jet. J. Fluid Mech. 258, 31–75.10.1017/S002211209400323XGoogle Scholar
Kataoka, I. & Serizawa, A. 1989 Basic equations of turbulence in gas–liquid two-phase flow. Intl J. Multiphase Flow 15, 843–855.10.1016/0301-9322(89)90045-1Google Scholar
Lai, C. C. K.2015 An analysis of bubble plumes in unstratified stagnant water. PhD thesis, Texas A&M University, USA.Google Scholar
Lai, C. C. K., Fraga, B., Dodd, M. & Chan, R. 2018 Energy cascade in a homogeneous swarm of bubbles rising in a vertical channel. In Proceedings of the Summmer Program 2018. Center for Turbulence Research, Stanford University.Google Scholar
Lai, C. C. K. & Socolofsky, S. A. 2018 Evaluation of linear autoregressive models for estimation of energy spectra in gappy turbulent velocity data. L&O Methods 16 (1), 1–21.Google Scholar
Lance, M. & Bataille, J. 1991 Turbulence in the liquid phase of a uniform bubbly air–water flow. J. Fluid Mech. 222, 95–118.10.1017/S0022112091001015Google Scholar
Lee, J. H. W. & Chu, V. H. 2003 Turbulent Jets and Plumes – a Lagrangian Approach. Kluwer Academic.10.1007/978-1-4615-0407-8Google Scholar
Lumley, J. L. 1978 Computational modeling of turbulent flows. Adv. Appl. Mech. 18, 123–176.10.1016/S0065-2156(08)70266-7Google Scholar
Ma, T., Santarelli, C., Ziegenhein, T., Lucas, D. & Frohlich, J. 2017 Direct numerical simulation-based Reynolds-averaged closure for bubble-induced turbulence. Phys. Rev. Fluids 2, 034301.10.1103/PhysRevFluids.2.034301Google Scholar
Mercado, J. M., Gomes, D. C., van Gils, D., Sun, C. & Lohse, D. 2010 On bubble clustering and energy spectra in pseudo-turbulence. J. Fluid Mech. 650, 287–306.10.1017/S0022112009993570Google Scholar
Milgram, J. H. 1983 Mean flow in round bubble plumes. J. Fluid Mech. 133, 345–376.10.1017/S0022112083001950Google Scholar
Milgram, J. H. & Van Houten, R. J. 1982 Plumes from sub-sea well blowouts. In Proceedings of the 3rd International Conference, BOSS, vol. I, pp. 659–684. MIT.Google Scholar
Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Nortek 2013 Vectrino Profiler – User Manual. Nortek AS.Google Scholar
Papanicolaou, P. N. & List, E. J. 1988 Investigations of round vertical buoyant jets. J. Fluid Mech. 195, 341–391.10.1017/S0022112088002447Google Scholar
Pope, S. B. 2000 Turbulent Flow. Cambridge University Press.10.1017/CBO9780511840531Google Scholar
Prakash, V. N., Mercado, J. M., van Wijngaarden, L., Mancilla, E., Tagawa, Y., Lohse, D. & Sun, C. 2016 Energy spectra in turbulent bubbly flows. J. Fluid Mech. 791, 174–190.10.1017/jfm.2016.49Google Scholar
Rensen, J., Luther, S. & Lohse, D. 2005 The effect of bubbles on developed turbulence. J. Fluid Mech. 538, 153–187.10.1017/S0022112005005276Google Scholar
Riboux, G., Legendre, D. & Risso, F. 2013 A model of bubble-induced turbulence based on large-scale wake interactions. J. Fluid Mech. 719, 362–387.10.1017/jfm.2013.12Google Scholar
Riboux, G., Risso, F. & Legendre, D. 2010 Experimental characterization of the agitation generated by bubbles rising at high Reynolds number. J. Fluid Mech. 643, 509–539.10.1017/S0022112009992084Google Scholar
Risso, F. 2018 Agitation, mixing, and transfers induced by bubbles. Annu. Rev. Fluid Mech. 50, 25–48.10.1146/annurev-fluid-122316-045003Google Scholar
Risso, F. & Ellingsen, K. 2002 Velocity fluctuations in a homogeneous dilute dispersion of high-Reynolds-number rising bubbles. J. Fluid Mech. 453, 395–410.10.1017/S0022112001006930Google Scholar
Roig, V. & de Tournemine, L. 2007 Measurement of interstitial velocity of homogeneous bubbly flows at low to moderate void fraction. J. Fluid Mech. 572, 87–110.10.1017/S0022112006003600Google Scholar
Santarelli, C., Roussel, J. & Frohlich, J. 2016 Budget analysis of the turbulent kinetic energy for bubbly flow in a vertical channel. Chem. Engng Sci. 141, 46–62.10.1016/j.ces.2015.10.013Google Scholar
Seol, D.-G., Bhaumik, T., Bergmann, C. & Socolofsky, S. A. 2007 Particle image velocimetry measurements of the mean flow characteristics in a bubble plume. J. Hydraul. Engng ASCE 133 (6), 665–676.10.1061/(ASCE)0733-9399(2007)133:6(665)Google Scholar
Seol, D.-G., Duncan, B. B. & Socolofsky, S. A. 2009 Measurements of behavioral properties of entrained ambient water in stratified bubble plume. J. Hydraul. Engng ASCE 135 (11), 983–988.10.1061/(ASCE)HY.1943-7900.0000109Google Scholar
Shabbir, A. & George, W. K. 1994 Experiments on a round turbulent buoyant plume. J. Fluid Mech. 275, 1–32.10.1017/S0022112094002260Google Scholar
Shawkat, M. E. & Chng, C. Y. 2011 Liquid turbulence kinetic energy budget of co-current bubbly flow in a large diameter vertical pipe. J. Fluids Engng 133, 091303.Google Scholar
Simiano, M., Lakehal, D., Lance, M. & Yadigaroglu, L. 2009 Turbulent transport mechanisms in oscillating bubble plumes. J. Fluid Mech. 633, 191–231.10.1017/S0022112009006971Google Scholar
Simiano, M., Zboray, R., de Cachard, F., Lakehal, D. & Yadigaroglu, L. 2006 Comprehensive experimental investigation of the hydrodyanmics of large-scale, three-dimensional bubble plumes. Intl J. Multiphase Flow 32 (10), 1160–1181.10.1016/j.ijmultiphaseflow.2006.05.014Google Scholar
Socolofsky, S. A., Adams, E. E. & Sherwood, C. R. 2011 Formation dynamics of subsurface hydrocarbon intrusions following the deepwater horizon blowout. Geophys. Res. Lett. 38, L09602.10.1029/2011GL047174Google Scholar
Socolofsky, S. A., Bhaumik, T. & Seol, D.-G. 2008 Double-plume integral models for near-field mixing in multiphase plumes. J. Hydraul. Engng ASCE 134 (6), 772–783.10.1061/(ASCE)0733-9429(2008)134:6(772)Google Scholar
Taub, G. N., Lee, H., Balachandar, S. & Sherif, S. A. 2013 A direction numerical simulation study of higher order statistics in a turbulent round jet. Phys. Fluids 25 (115102), 1–19.10.1063/1.4829045Google Scholar
Taylor, G. I. 1935 Statistical theory of turbulence. Proc. R. Soc. Lond. A 151, 421–444.10.1098/rspa.1935.0158Google Scholar
Torrence, C. & Compo, G. P. 1998 A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 79 (1), 61–78.10.1175/1520-0477(1998)079<0061:APGTWA>2.0.CO;22.0.CO;2>Google Scholar
Vaidheeswaran, A. & Hibiki, T. 2017 Bubble-induced turbulence modeling for vertical bubbly flows. Intl J. Heat Mass Transfer 115, 741–752.10.1016/j.ijheatmasstransfer.2017.08.075Google Scholar
Voulgaris, G. & Trowbridge, J. H. 1998 Evaluation of the acoustic Doppler velocimeter for turbulence measurements. J. Atmos. Ocean. Technol. 15, 272–289.10.1175/1520-0426(1998)015<0272:EOTADV>2.0.CO;22.0.CO;2>Google Scholar
Wang, B., Socolofsky, S. A., Breier, J. A. & Seewald, J. S. 2016 Observations of bubbles in natural seep flares at mc 118 and gc 600 using in situ quantitative imaging. J. Geophys. Res. Oceans 121, 2203–2230.10.1002/2015JC011452Google Scholar
Wang, H. & Law, A. W. K 2002 Second-order integral model for a round turbulent buoyant jet. J. Fluid Mech. 459, 397–428.10.1017/S0022112002008157Google Scholar
Wuest, A., Brooks, N. H. & Imboden, D. M. 1992 Bubble plume modelling for lake restoration. Water Resour. Res. 28 (12), 3235–3250.10.1029/92WR01681Google Scholar