Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T14:57:42.775Z Has data issue: false hasContentIssue false
  • English
  • Français

The turbulent Kármán vortex

Published online by Cambridge University Press:  17 May 2019

J. G. Chen Open the ORCID record for J. G. Chen [Opens in a new window] ,
Y. Zhou ,
R. A. Antonia  and
T. M. Zhou
J. G. Chen
Affiliation:
Institute for Turbulence-Noise-Vibration Interactions and Control, Harbin Institute of Technology (Shenzhen), Shenzhen 518055, PR China Digital Engineering Laboratory of Offshore Equipment, Shenzhen 518055, PR China
Y. Zhou*
Affiliation:
Institute for Turbulence-Noise-Vibration Interactions and Control, Harbin Institute of Technology (Shenzhen), Shenzhen 518055, PR China Digital Engineering Laboratory of Offshore Equipment, Shenzhen 518055, PR China
R. A. Antonia
Affiliation:
School of Engineering, University of Newcastle, NSW 2308, Australia
T. M. Zhou
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, WA 6009, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This work focuses on the temperature (passive scalar) and velocity characteristics within a turbulent Kármán vortex using a phase-averaging technique. The vortices are generated by a circular cylinder, and the three components of the fluctuating velocity and vorticity vectors, 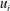$u_{i}$ and 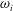$\unicode[STIX]{x1D714}_{i}$ (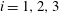$i=1,2,3$), are simultaneously measured, along with the fluctuating temperature 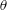$\unicode[STIX]{x1D703}$ and the temperature gradient vector, at nominally the same spatial point in the plane of mean shear at 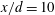$x/d=10$, where $x$ is the streamwise distance from the cylinder axis and 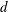$d$ is the cylinder diameter. We believe this is the first time the properties of fluctuating velocity, temperature, vorticity and temperature gradient vectors have been explored simultaneously within the Kármán vortex in detail. The Reynolds number based on 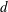$d$ and the free-stream velocity is 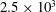$2.5\times 10^{3}$. The phase-averaged distributions of 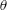$\unicode[STIX]{x1D703}$ and 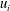$u_{i}$ follow closely the Gaussian distribution for 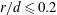$r/d\leqslant 0.2$ ($r$ is the distance from the vortex centre), but not for 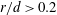$r/d>0.2$. The collapse of the distributions of the mean-square streamwise derivative of the velocity fluctuations within the Kármán vortex implies that the velocity field within the vortex tends to be more locally isotropic than the flow field outside the vortex. A possible physical explanation is that the large and small scales of velocity and temperature fields are statistically independent of each other near the Kármán vortex centre, but interact vigorously outside the vortex, especially in the saddle region, due to the action of coherent strain rate.

JFM classification

Vortex Flows: Vortex dynamics Wakes/Jets: Vortex streets Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 871 , 25 July 2019 , pp. 92 - 112
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A., Chambers, A. J., Britz, D. & Browne, L. 1986 Organized structures in a turbulent plane jet: topology and contribution to momentum and heat transport. J. Fluid Mech. 172, 211–229.Google Scholar
Antonia, R. A., Chambers, A. J., Van Atta, C. W., Friehe, C. A. & Helland, K. N. 1978 Skewness of temperature derivative in a heated grid flow. Phys. Fluids 21, 509–510.Google Scholar
Antonia, R. A., Djenidi, L. & Danaila, L. 2014 Collapse of the turbulent dissipative range on Kolmogorov scales. Phys. Fluids 26, 045105.Google Scholar
Batchelor, G. K. 1951 Pressure fluctuations in isotropic turbulence. Math. Proc. Camb. Phil. Soc. 47, 359–374.Google Scholar
Browne, L., Antonia, R. A. & Shah, D. A. 1987 Turbulent energy dissipation in a wake. J. Fluid Mech. 179, 307–326.Google Scholar
Cantwell, B. & Coles, D. 1983 An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J. Fluid Mech. 136, 321–374.Google Scholar
Chen, J. G., Zhou, Y., Antonia, R. A. & Zhou, T. M. 2018 Characteristics of the turbulent energy dissipation rate in a cylinder wake. J. Fluid Mech. 835, 271–300.Google Scholar
Chen, J. G., Zhou, Y., Zhou, T. M. & Antonia, R. A. 2016 Three-dimensional vorticity, momentum and heat transport in a turbulent cylinder wake. J. Fluid Mech. 809, 135–167.Google Scholar
Cossin, S.1943 Investigation of flow in an axially symmetrical heated jet of air. Tech. Rep. NACA-WR-W-94.Google Scholar
Davidson, P. 2015 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Djenidi, L. & Antonia, R. A. 2009 Momentum and heat transport in a three-dimensional transitional wake of a heated square cylinder. J. Fluid Mech. 640, 109–129.Google Scholar
Gibson, C. H., Friehe, C. A. & McConnell, S. O. 1977 Structure of sheared turbulent fields. Phys. Fluids 20, S156.Google Scholar
Granger, R. A. 1985 Fluid Mechanics. CBS College Publishing.Google Scholar
Hangan, H. 2018 Large scale physical simulations of 3D, non-stationary and non-Gaussian wind flows with applications to moving/deformable structures. In IUTAM Symposium on Critical Flow Dynamics involving Moving/Deformable Structures with Design Applications, June 18–22, Santorini, Greece.Google Scholar
Hayakawa, M. & Hussain, F. 1989 Three-dimensionality of organized structures in a plane turbulent wake. J. Fluid Mech. 206, 375–404.Google Scholar
Holzer, M. & Siggia, E. D. 1994 Turbulent mixing of a passive scalar. Phys. Fluids. 6, 1820–1837.Google Scholar
Hu, H., Yang, Z., Sarkar, P. & Haan, F. 2011 Characterization of the wind loads and flow fields around a gable-roof building model in tornado-like winds. Exp. Fluids 51, 835–851.Google Scholar
Hussain, A. K. M. F. & Hayakawa, M. 1987 Eduction of large-scale organized structures in a turbulent plane wake. J. Fluid Mech. 180, 193–229.Google Scholar
Jiménez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.Google Scholar
Kiya, M. & Matsumura, M. 1988 Incoherent turbulence structure in the near wake of a normal plate. J. Fluid Mech. 190, 343–356.Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Landau, L. D. & Lifschitz, E. M. 1987 Fluid Mechanics. Elsevier/Butterworth-Heinemann.Google Scholar
Lefeuvre, N., Thiesset, F., Djenidi, L. & Antonia, R. A. 2014 Statistics of the turbulent kinetic energy dissipation rate and its surrogates in a square cylinder wake flow. Phys. Fluids 26, 095104.Google Scholar
Matsumura, M. & Antonia, R. A. 1993 Momentum and heat transport in the turbulent intermediate wake of a circular cylinder. J. Fluid Mech. 250, 651–668.Google Scholar
Mi, J. & Antonia, R. A. 2010 Approach to local axisymmetry in a turbulent cylinder wake. Exp. Fluids 48, 933–947.Google Scholar
Pearson, B. R. & Antonia, R. A. 2001 Reynolds-number dependence of turbulent velocity and pressure increments. J. Fluid Mech. 444, 343–382.Google Scholar
Pumir, A. 1994 A numerical study of the mixing of a passive scalar in three dimensions in the presence of a mean gradient. Phys. Fluids 6, 2118–2132.Google Scholar
Shafi, H. S. & Antonia, R. A. 1997 Small-scale characteristics of a turbulent boundary layer over a rough wall. J. Fluid Mech. 342, 263–293.Google Scholar
She, Z.-S., Jackson, E. & Orszag, S. A. 1991 Structure and dynamics of homogeneous turbulence: models and simulations. Proc. R. Soc. Math. Phys. Engng Sci. 434, 101–124.Google Scholar
Shraiman, B. I. & Siggia, E. D. 2000 Scalar turbulence. Nature 405, 639–646.Google Scholar
Sreenivasan, K. R. 1991 On local isotropy of passive scalars in turbulent shear flows. Proc. R. Soc. Lond. A 434, 165–182.Google Scholar
Sreenivasan, K. R. & Antonia, R. A. 1977 Skewness of temperature derivatives in turbulent shear flows. Phys. Fluids 20, 1986–1988.Google Scholar
Taylor, G. I. 1935 Statistical theory of turbulence. Proc. R. Soc. Math. Phys. Engng Sci. 151, 421–444.Google Scholar
Tong, C. & Warhaft, Z. 1994 On passive scalar derivative statistics in grid turbulence. Phys. Fluids 6, 2165–2176.Google Scholar
Watanabe, T. & Gotoh, T. 2004 Statistics of a passive scalar in homogeneous turbulence. New J. Phys. 6, 40.Google Scholar
Warhaft, Z. 2000 Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 32, 203–240.Google Scholar
Williamson, C. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Yang, Z., Sarkar, P. & Hu, H. 2011 An experimental study of a high-rise building model in tornado-like winds. J. Fluids Struct. 27, 471–486.Google Scholar
Zhou, T., Pearson, B. R. & Antonia, R. A. 2001 Comparison between temporal and spatial transverse velocity increments in a turbulent plane jet. Fluid Dyn. Res. 28, 127–138.Google Scholar
Zhou, T., Razali, S. M., Zhou, Y., Chua, L. P. & Cheng, L. 2009 Dependence of the wake on inclination of a stationary cylinder. Exp. Fluids 46, 1125–1138.Google Scholar
Zhou, T., Zhou, Y., Yiu, M. W. & Chua, L. P. 2003 Three-dimensional vorticity in a turbulent cylinder wake. Exp. Fluids 35, 459–471.Google Scholar
Zhou, Y. & Antonia, R. A. 1992 Convection velocity measurements in a cylinder wake. Exp. Fluids 13, 63–70.Google Scholar
Zhou, Y. & Antonia, R. A. 1993 A study of turbulent vortices in the near wake of a cylinder. J. Fluid Mech. 253, 643–661.Google Scholar
Zhou, Y. & Antonia, R. A. 1994 Critical points in a turbulent near-wake. J. Fluid Mech. 275, 59–81.Google Scholar
Zhu, Y. & Antonia, R. A. 1996 Spatial resolution of a 4-X-wire vorticity probe. Meas. Sci. Technol. 7, 1492–1497.Google Scholar