Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-27T19:55:22.346Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent flow through a high aspect ratio cooling duct with asymmetric wall heating

Published online by Cambridge University Press:  04 December 2018

Thomas Kaller Open the ORCID record for Thomas Kaller [Opens in a new window] ,
Vito Pasquariello Open the ORCID record for Vito Pasquariello [Opens in a new window] ,
Stefan Hickel Open the ORCID record for Stefan Hickel [Opens in a new window]  and
Nikolaus A. Adams
Thomas Kaller*
Affiliation:
Technical University of Munich, Department of Mechanical Engineering, Chair of Aerodynamics and Fluid Mechanics, Boltzmannstr. 15, D-85748 Garching bei München, Germany
Vito Pasquariello
Affiliation:
Technical University of Munich, Department of Mechanical Engineering, Chair of Aerodynamics and Fluid Mechanics, Boltzmannstr. 15, D-85748 Garching bei München, Germany
Stefan Hickel
Affiliation:
Faculty of Aerospace Engineering, Technische Universiteit Delft, Kluyverweg 1, 2629 HT Delft, The Netherlands
Nikolaus A. Adams
Affiliation:
Technical University of Munich, Department of Mechanical Engineering, Chair of Aerodynamics and Fluid Mechanics, Boltzmannstr. 15, D-85748 Garching bei München, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present well-resolved large-eddy simulations of turbulent flow through a straight, high aspect ratio cooling duct operated with water at a bulk Reynolds number of 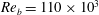$Re_{b}=110\times 10^{3}$ and an average Nusselt number of 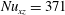$Nu_{xz}=371$. The geometry and boundary conditions follow an experimental reference case and good agreement with the experimental results is achieved. The current investigation focuses on the influence of asymmetric wall heating on the duct flow field, specifically on the interaction of turbulence-induced secondary flow and turbulent heat transfer, and the associated spatial development of the thermal boundary layer and the inferred viscosity variation. The viscosity reduction towards the heated wall causes a decrease in turbulent mixing, turbulent length scales and turbulence anisotropy as well as a weakening of turbulent ejections. Overall, the secondary flow strength becomes increasingly less intense along the length of the spatially resolved heated duct as compared to an adiabatic duct. Furthermore, we show that the assumption of a constant turbulent Prandtl number is invalid for turbulent heat transfer in an asymmetrically heated duct.

JFM classification

Boundary Layers: Pipe flow boundary layer Turbulent Flows: Turbulent Flows Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 860 , 10 February 2019 , pp. 258 - 299
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baines, W. D. & Brundrett, E. 1964 The production and diffusion of vorticity in duct flow. J. Fluid Mech. 19, 375–394.Google Scholar
Banerjee, S., Krahl, R., Durst, F. & Zenger, C. 2007 Presentation of anisotropy properties of turbulence, invariants versus eigenvalue approaches. J. Turbul. 8 (32), 1–27.Google Scholar
Choi, H. S. & Park, T. S. 2013 The influence of streamwise vortices on turbulent heat transfer in rectangular ducts with various aspect ratios. Intl J. Heat Fluid Flow 40, 1–14.Google Scholar
Choi, K.-S. & Lumley, J. L. 2001 The return to isotropy of homogeneous turbulence. J. Fluid Mech. 436, 59–84.Google Scholar
Demuren, A. O. & Rodi, W. 1984 Calculation of turbulence-driven secondary motion in non-circular ducts. J. Fluid Mech. 140, 189–222.Google Scholar
Emory, M. & Iaccarino, G. 2014 Visualizing turbulence anisotropy in the spatial domain with componentality contours. In Annual Research Briefs, Center for Turbulence Research, Stanford University, pp. 123–138.Google Scholar
Gavrilakis, S. 1992 Numerical simulation of low-Reynolds-number turbulent flow through a straight square duct. J. Fluid Mech. 244, 101–129.Google Scholar
Gessner, F. B. & Jones, J. B. 1965 On some aspects of fully-developed turbulent flow in rectangular channels. J. Fluid Mech. 23 (4), 689–713.Google Scholar
Gottlieb, S. & Shu, C. 1998 Total variation diminishing Runge–Kutta schemes. Maths Comput. 67 (221), 73–85.Google Scholar
Grilli, M., Schmid, P. J., Hickel, S. & Adams, N. A. 2012 Analysis of unsteady behaviour in shockwave turbulent boundary layer interaction. J. Fluid Mech. 700, 16–28.Google Scholar
Hébrard, J., Métais, O. & Salinas-Vásquez, M. 2004 Large-eddy simulation of turbulent duct flow: heating and curvature effects. Intl J. Heat Fluid Flow 25 (4), 569–580.Google Scholar
Hébrard, J., Salinas-Vásquez, M. & Métais, O. 2005 Spatial development of turbulent flow within a heated duct. J. Turbul. 6, N8.Google Scholar
Hickel, S. & Adams, N. A. 2007 On implicit subgrid-scale modeling in wall-bounded flows. Phys. Fluids 19, 105106.Google Scholar
Hickel, S. & Adams, N. A. 2008 Implicit LES applied to zero-pressure-gradient and adverse-pressure-gradient boundary-layer turbulence. Intl J. Heat Fluid Flow 29, 626–639.Google Scholar
Hickel, S., Adams, N. A. & Domaradzki, J. A. 2006 An adaptive local deconvolution method for implicit LES. J. Comput. Phys. 213 (1), 413–436.Google Scholar
Hickel, S., Adams, N. A. & Mansour, N. N. 2007 Implicit subgrid-scale modeling for large-eddy simulation of passive-scalar mixing. Phys. Fluids 19 (9), 095102.Google Scholar
Hirota, M., Fujita, H., Yokosawa, H., Nakai, H. & Itoh, H. 1997 Turbulent heat transfer in a square duct. Intl J. Heat Fluid Flow 18 (1), 170–180.Google Scholar
Huser, A. & Biringen, S. 1993 Direct numerical simulation of turbulent flow in a square duct. J. Fluid Mech. 257, 65–95.Google Scholar
IAPWS 2008 Release on the IAPWS formulation 2008 for the viscosity of ordinary water substance. The International Association for the Properties of Water and Steam (IAPWS). Available from http://www.iapws.org.Google Scholar
IAPWS 2011 Release on the IAPWS formulation 2011 for the thermal conductivity of ordinary water substance. The International Association for the Properties of Water and Steam (IAPWS). Available from http://www.iapws.org.Google Scholar
Kaller, T., Pasquariello, V., Hickel, S. & Adams, N. A. 2017 Large-eddy simulation of the high-Reynolds-number flow through a high-aspect-ratio cooling duct. In Proceedings of the 10th International Symposium on Turbulence and Shear Flow Phenomena (TSFP-10), Chicago, USA.Google Scholar
Kang, S. & Iaccarino, G. 2010 Computation of turbulent Prandtl number for mixed convection around a heated cylinder. In Annual Research Briefs, Center for Turbulence Research, Stanford University, pp. 295–304.Google Scholar
Kays, W. M. 1994 Turbulent Prandtl number – where are we? Trans. ASME J. Heat Transfer 116 (2), 284–295.Google Scholar
Launder, B. E. & Ying, W. M. 1972 Secondary flows in ducts of square cross-section. J. Fluid Mech. 54 (2), 289–295.Google Scholar
Lee, J., Jung, S. Y., Sung, H. J. & Zaki, T. A. 2013 Effect of wall heating on turbulent boundary layers with temperature-dependent viscosity. J. Fluid Mech. 726, 196–225.Google Scholar
Lumley, J. L. 1978 Computational modeling of turbulent flows. Adv. Appl. Mech. 18, 123–176.Google Scholar
Madabhushi, R. K. & Vanka, S. P. 1991 Large eddy simulation of turbulence-driven secondary flow in a square duct. Phys. Fluids A 3 (11), 2734–2745.Google Scholar
Melling, A. & Whitelaw, J. H. 1976 Turbulent flow in a rectangular duct. J. Fluid Mech. 78 (2), 289–315.Google Scholar
Monin, A. S., Yaglom, A. M. & Lumley, J. L. 2007 Statistical Fluid Mechanics, Volume II: Mechanics of Turbulence. Dover.Google Scholar
Monty, J. P.2005 Developments in smooth wall turbulent duct flows. PhD thesis, The University of Melbourne.Google Scholar
Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.Google Scholar
O’Neill, P. L., Nicolaides, D., Honnery, D. & Soria, J. 2004 Autocorrelation functions and the determination of integral length with reference to experimental and numerical data. In Proceedings of the Fifteenth Australasian Fluid Mechanics Conference (ed. Behnia, M., Lin, W. & McBain, G. D.). The University of Sydney.Google Scholar
Pallares, J. & Davidson, L. 2002 Large-eddy simulations of turbulent heat transfer in stationary and rotating square ducts. Phys. Fluids 14 (8), 2804–2816.Google Scholar
Pasquariello, V., Grilli, M., Hickel, S. & Adams, N. A. 2014 Large-eddy simulation of passive shock-wave/boundary-layer interaction control. Intl J. Heat Fluid Flow 49, 116–127.Google Scholar
Pasquariello, V., Hickel, S. & Adams, N. A. 2017 Unsteady effects of strong shock-wave/boundary-layer interaction at high Reynolds number. J. Fluid Mech. 823, 617–657.Google Scholar
Patel, A., Boersma, B. J. & Pecnik, R. 2016 The influence of near-wall density and viscosity gradients on turbulence in channel flows. J. Fluid Mech. 809, 793–820.Google Scholar
Pinelli, A., Uhlmann, M., Sekimoto, A. & Kawahara, G. 2010 Reynolds number dependence of mean flow structure in square duct turbulence. J. Fluid Mech. 644, 107–122.Google Scholar
Pirozzoli, S., Grasso, F. & Gatski, T. B. 2004 Direct numerical simulation and analysis of a spatially evolving supersonic turbulent boundary layer at M = 2. 25. Phys. Fluids 16 (3), 530–545.Google Scholar
Pirozzoli, S., Modesti, D., Orlandi, P. & Grasso, F. 2018 Turbulence and secondary motions in square duct flow. J. Fluid Mech. 840, 631–655.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Qin, Z. & Pletcher, R. H. 2006 Large eddy simulation of turbulent heat transfer in a rotating square duct. Intl J. Heat Fluid Flow 27, 371–390.Google Scholar
Quaatz, J. F., Giglmaier, M., Hickel, S. & Adams, N. A. 2014 Large-eddy simulation of a pseudo-shock system in a Laval nozzle. Intl J. Heat Fluid Flow 49, 108–115.Google Scholar
Remmler, S. & Hickel, S. 2012 Direct and large eddy simulation of stratified turbulence. Intl J. Heat Fluid Flow 35, 13–24.Google Scholar
Rochlitz, H., Scholz, P. & Fuchs, T. 2015 The flow field in a high aspect ratio cooling duct with and without one heated wall. Exp. Fluids 56 (12), 1–13.Google Scholar
Salinas-Vásquez, M. & Métais, O. 2002 Large-eddy simulation of the turbulent flow through a heated square duct. J. Fluid Mech. 453, 201–238.Google Scholar
Salinas-Vásquez, M., Vicente Rodríguez, W. & Issa, R. 2005 Effects of ridged walls on the heat transfer in a heated square duct. Intl J. Heat Mass Transfer 48 (10), 2050–2063.Google Scholar
Sameen, A. & Govindarajan, R. 2007 The effect of wall heating on instability of channel flow. J. Fluid Mech. 577, 417–442.Google Scholar
Sekimoto, A., Kawahara, G., Sekiyama, K., Uhlmann, M. & Pinelli, A. 2011 Turbulence- and buoyancy-driven secondary flows in a horizontal square duct heated from below. Phys. Fluids 23 (7), 075103.Google Scholar
Shah, R. K. & London, A. L. 1978 Laminar Flow Forced Convection in Ducts. Academic Press.Google Scholar
Simonsen, A. J. & Krogstad, P. Å. 2005 Turbulent stress invariant analysis: clarification of existing terminology. Phys. Fluids 17 (8), 1–4.Google Scholar
Vidal, A., Vinuesa, R., Schlatter, P. & Nagib, H. M. 2017a Impact of corner geometry on the secondary flow in turbulent ducts. In Proceedings of the 10th International Symposium on Turbulence and Shear Flow Phenomena (TSFP-10), Chicago, USA.Google Scholar
Vidal, A., Vinuesa, R., Schlatter, P. & Nagib, H. M. 2017b Influence of corner geometry on the secondary flow in turbulent square ducts. Intl J. Heat Fluid Flow 67, 69–78.Google Scholar
Vinuesa, R., Noorani, A., Lozano-Duran, A., El Khoury, G., Schlatter, P., Fischer, P. F. & Nagib, N. M. 2014 Aspect ratio effects in turbulent duct flows studied through direct numerical simulation. J. Turbul. 15 (10), 677–706.Google Scholar
Wallace, J. M. 2016 Quadrant analysis in turbulence research: history and evolution. Annu. Rev. Fluid Mech. 48 (1), 131–158.Google Scholar
Wallace, J. M., Eckelmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54 (1), 39–48.Google Scholar
Wardana, I. N. G., Ueda, T. & Mizomoto, M. 1994 Effect of strong wall heating on turbulence statistics of a channel flow. Exp. Fluids 18 (1), 87–94.Google Scholar
Willmarth, W. W. & Lu, S. S. 1972 Structure of the Reynolds stress near the wall. J. Fluid Mech. 55 (1), 65–92.Google Scholar
Yang, H., Chen, T. & Zhu, Z. 2009 Numerical study of forced turbulent heat convection in a straight square duct. Intl J. Heat Mass Transfer 52 (13–14), 3128–3136.Google Scholar
Zhang, H., Xavier Trias, F., Gorobets, A., Tan, Y. & Oliva, A. 2015 Direct numerical simulation of a fully developed turbulent square duct flow up to Re 𝜏 = 1200. Intl J. Heat Fluid Flow 54, 258–267.Google Scholar
Zhu, Z., Yang, H. & Chen, T. 2010 Numerical study of turbulent heat and fluid flow in a straight square duct at higher Reynolds numbers. Intl J. Heat Mass Transfer 53 (1–3), 356–364.Google Scholar
Zonta, F., Marchioli, C. & Soldati, A. 2012 Modulation of turbulence in forced convection by temperature-dependent viscosity. J. Fluid Mech. 697, 150–174.Google Scholar