Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-01T00:58:33.188Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent flow of a fluid with anisotropic viscosity

Published online by Cambridge University Press:  01 March 2016

Tim Grünberg  and
Thomas Rösgen
Tim Grünberg
Affiliation:
Institute of Fluid Dynamics, ETH Zürich, 8092 Zürich, Switzerland
Thomas Rösgen*
Affiliation:
Institute of Fluid Dynamics, ETH Zürich, 8092 Zürich, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We ask if and how the large-scale structure of a turbulent flow depends on anisotropies introduced at the smallest scales. We generate such anisotropy on the viscous scale in a paramagnetic colloid whose rheology is modified by an external, uniform magnetic field. We report measurements in a high Reynolds number turbulence experiment (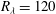$R_{{\it\lambda}}=120$). Ultrasound velocimetry provides records of tracer particle velocity. Distinct changes in the velocity statistics can be observed from the dissipative scales up to the mean flow topology.

JFM classification

MHD and Electrohydrodynamics: Magnetic fluids MHD and Electrohydrodynamics: MHD and Electrohydrodynamics Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 792 , 10 April 2016 , pp. 252 - 273
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altmeyer, S., Hoffmann, C., Leschhorn, A. & Lücke, M. 2010 Influence of homogeneous magnetic fields on the flow of a ferrofluid in the Taylor–Couette system. Phys. Rev. E 82, 016321.Google Scholar
Benzi, R., Ciliberto, S., Tripiccione, R., Baudet, C., Massaioli, F. & Succi, S. 1993 Extended self-similarity in turbulent flows. Phys. Rev. E 48, R29–R32.Google Scholar
Borin, D., Zubarev, A., Chirikov, D., Müller, R. & Odenbach, S. 2011 Ferrofluid with clustered iron nanoparticles: Slow relaxation of rheological properties under joint action of shear flow and magnetic field. J. Magn. Magn. Mater. 323 (10), 1273–1277.CrossRefGoogle Scholar
Brown, R. D., Warhaft, Z. & Voth, G. A. 2009 Acceleration statistics of neutrally buoyant spherical particles in intense turbulence. Phys. Rev. Lett. 103, 194501.CrossRefGoogle ScholarPubMed
Chang, K., Bewley, G. P. & Bodenschatz, E. 2012 Experimental study of the influence of anisotropy on the inertial scales of turbulence. J. Fluid Mech. 692, 464–481.CrossRefGoogle Scholar
Conway, J. T. 2006 Trigonometric integrals for the magnetic field of the coil of rectangular cross section. IEEE Trans. Magn. 42 (5), 1538–1548.CrossRefGoogle Scholar
Douady, S., Couder, Y. & Brachet, M. E. 1991 Direct observation of the intermittency of intense vorticity filaments in turbulence. Phys. Rev. Lett. 67, 983–986.Google Scholar
Elsinga, G. E. & Marusic, I. 2016 The anisotropic structure of turbulence and its energy spectrum. Phys. Fluids 28 (1), 011701.CrossRefGoogle Scholar
Ericksen, J. L. 1960 Transversely isotropic fluids. Kolloid Z. 173 (2), 117–122.Google Scholar
Ilg, P. & Kröger, M. 2002 Magnetization dynamics, rheology, and an effective description of ferromagnetic units in dilute suspension. Phys. Rev. E 66, 021501.CrossRefGoogle Scholar
Ishihara, T., Yoshida, K. & Kaneda, Y. 2002 Anisotropic velocity correlation spectrum at small scales in a homogeneous turbulent shear flow. Phys. Rev. Lett. 88, 154501.Google Scholar
Kalman, R. E. 1960 A new approach to linear filtering and prediction problems. Trans. ASME J. Basic Engng 82 (1), 35–45.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941 Dokl. Akad. Nauk SSSR 30 (4), 299–303; [in Russian]. English translation by Levin. V The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. R. Soc. Lond. A (1991) 434 (1890) 9–13.Google Scholar
Kraichnan, R. H. 1967 Inertial ranges in two dimensional turbulence. Phys. Fluids 10 (7), 1417–1423.CrossRefGoogle Scholar
Lamriben, C., Cortet, P.-P. & Moisy, F. 2011 Direct measurements of anisotropic energy transfers in a rotating turbulence experiment. Phys. Rev. Lett. 107, 024503.CrossRefGoogle Scholar
Leslie, F. M. 1966 Some constitutive equations for anisotropic fluids. Q. J. Mech. Appl. Maths 19 (3), 357–370.Google Scholar
Linke, J. M. & Odenbach, S. 2015 Anisotropy of the magnetoviscous effect in a ferrofluid with weakly interacting magnetite nanoparticles. J. Phys.: Condens. Matter 27 (17), 176001.Google Scholar
Maurer, J., Tabeling, P. & Zocchi, G. 1994 Statistics of turbulence between two counterrotating disks in low-temperature helium gas. Europhys. Lett. 26 (1), 31.Google Scholar
Mordant, N., Crawford, A. M. & Bodenschatz, E. 2004a Experimental Lagrangian acceleration probability density function measurement. Physica D 193, 245–251.CrossRefGoogle Scholar
Mordant, N., Lévêque, E. & Pinton, J.-F. 2004b Experimental and numerical study of the Lagrangian dynamics of high Reynolds turbulence. New J. Phys. 6, 116.CrossRefGoogle Scholar
Mordant, N., Metz, P., Pinton, J.-F. & Michel, O. 2005 Acoustical technique for Lagrangian velocity measurement. Rev. Sci. Instrum. 76, 025105.Google Scholar
Odenbach, S. 2004 Recent progress in magnetic fluid research. J. Phys.: Condens. Matter 16 (32), R1135.Google Scholar
Ott, S. & Mann, J. 2005 An experimental test of Corrsin’s conjecture and some related ideas. New J. Phys. 7 (1), 142.CrossRefGoogle Scholar
Ouellette, N. T., Xu, H. & Bodenschatz, E. 2009 Bulk turbulence in dilute polymer solutions. J. Fluid Mech. 629, 375–385.Google Scholar
Piomelli, U., Cabot, W. H., Moin, P. & Lee, S. 1991 Subgrid scale backscatter in turbulent and transitional flows. Phys. Fluids A 3 (7), 1766–1771.Google Scholar
Ravelet, F., Chiffaudel, A. & Daviaud, F. 2008 Supercritical transition to turbulence in an inertially driven von Kármán closed flow. J. Fluid Mech. 601, 339–364.Google Scholar
Ravelet, F., Marié, L., Chiffaudel, A. & Daviaud, F. 2004 Multistability and memory effect in a highly turbulent flow: Experimental evidence for a global bifurcation. Phys. Rev. Lett. 93, 164501.Google Scholar
Reindl, M. & Odenbach, S. 2011 Influence of a homogeneous axial magnetic field on Taylor–Couette flow of ferrofluids with low particle–particle interaction. Exp. Fluids 50, 375–384.CrossRefGoogle Scholar
Richardson, L. F. 1922 Weather Prediction by Numerical Process. Cambridge University Press.Google Scholar
Saint-Michel, B., Dubrulle, B., Marié, L., Ravelet, F. & Daviaud, F. 2013 Evidence for forcing-dependent steady states in a turbulent swirling flow. Phys. Rev. Lett. 111, 234502.Google Scholar
Sawford, B. L. 1991 Reynolds number effects in Lagrangian stochastic models of turbulent dispersion. Phys. Fluids A 3 (6), 1577–1586.Google Scholar
Sawford, B. L. & Yeung, P. K. 2011 Kolmogorov similarity scaling for one-particle Lagrangian statistics. Phys. Fluids 23 (9), 091704.CrossRefGoogle Scholar
Sawford, B. L., Yeung, P. K., Borgas, M. S., Vedula, P., La Porta, A., Crawford, A. M. & Bodenschatz, E. 2003 Conditional and unconditional acceleration statistics in turbulence. Phys. Fluids 15 (11), 3478–3489.Google Scholar
Schmidt, R. O. 1986 Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 34 (3), 276–280.Google Scholar
Shen, P. & Yeung, P. K. 1997 Fluid particle dispersion in homogeneous turbulent shear flow. Phys. Fluids 9 (11), 3472–3484.Google Scholar
Shen, X. & Warhaft, Z. 2000 The anisotropy of the small scale structure in high Reynolds number ( $R_{{\it\lambda}}\sim 1000$ ) turbulent shear flow. Phys. Fluids 12 (11), 2976–2989.Google Scholar
Sreekumari, A. & Ilg, P. 2015 Anisotropy of magnetoviscous effect in structure-forming ferrofluids. Phys. Rev. E 92, 012306.Google Scholar
Tennekes, H. 1975 Eulerian and Lagrangian time microscales in isotropic turbulence. J. Fluid Mech. 67, 561–567.Google Scholar
de la Torre, A. & Burguete, J. 2007 Slow dynamics in a turbulent von Kármán swirling flow. Phys. Rev. Lett. 99, 054101.Google Scholar
Vedula, P. & Yeung, P. K. 1999 Similarity scaling of acceleration and pressure statistics in numerical simulations of isotropic turbulence. Phys. Fluids 11 (5), 1208–1220.Google Scholar
Voth, G. A., La Porta, A., Crawford, A. M., Alexander, J. & Bodenschatz, E. 2002 Measurement of particle accelerations in fully developed turbulence. J. Fluid Mech. 469, 121–160.Google Scholar
Yeung, P. K. & Brasseur, J. G. 1991 The response of isotropic turbulence to isotropic and anisotropic forcing at the large scales. Phys. Fluids A 3 (5), 884–897.Google Scholar
Yeung, P. K. & Pope, S. B. 1989 Lagrangian statistics from direct numerical simulations of isotropic turbulence. J. Fluid Mech. 207, 531–586.Google Scholar
Yeung, P. K., Pope, S. B. & Sawford, B. L. 2006 Reynolds number dependence of Lagrangian statistics in large numerical simulations of isotropic turbulence. J. Turbul. 7, N58.Google Scholar