Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T05:36:42.854Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent flow in the bulk of Rayleigh–Bénard convection: aspect-ratio dependence of the small-scale properties

Published online by Cambridge University Press:  10 April 2014

Matthias Kaczorowski ,
Kai-Leong Chong  and
Ke-Qing Xia
Matthias Kaczorowski
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
Kai-Leong Chong
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
Ke-Qing Xia*
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Geometrical confinement of turbulent Rayleigh–Bénard convection (RBC) in Cartesian geometries is found to reduce the local Bolgiano length scale in the centre of the cell 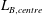$L_{B,centre}$ and can therefore be used to study cascade processes in the bulk of RBC. The dependence of 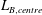$L_{B,centre}$ versus 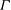$\varGamma $ suggests a cut-off to the local 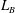$L_B$, which depends on the Prandtl number 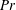$Pr$ and is of the order of the cell’s smallest dimension. It is also observed that geometrical confinement changes the topology of the flow, causing the turbulent kinetic energy dissipation rate and the temperature variance dissipation rate (averaged over the centre of the cell and normalized by their respective global averages) to exhibit a maximum at a certain 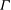$\varGamma $, which roughly coincides with the aspect ratio at which the viscous and thermal boundary layers of the two opposite lateral walls merge. As a result the mean heat flux through the core region also exhibits a maximum. Unlike in the cubic case, we find that geometrical confinement of the flow results in a local balance of the heat flux and the turbulent kinetic energy dissipation rate for 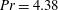$Pr= 4.38$ for all values of the Rayleigh number 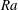$Ra$ (up to 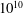$10^{10}$), while no balance is observed for 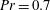$Pr= 0.7$. The need for very high bulk resolution to accurately resolve the gradients of the flow field at high 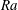$Ra$ is shown by analysing the second-order structure functions of the vertical velocity and temperature in the bulk of RBC. Under-resolution of the temperature field yields a large error in the dissipative range scaling, which is believed to be an effect of intermittently penetrating thermal plumes. The resolution contrast resulting from the requirement to resolve the thermal plumes and the homogeneous and isotropic background turbulence scales as 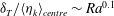$\delta _T / \langle \eta _k \rangle _{centre} \sim Ra^{0.1}$ and should therefore be taken into account when tackling very high 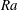$Ra$. In the case studied here, under-resolution can have a significant effect on the local heat flux through the centre of the cell.

JFM classification

Turbulent Flows: Turbulent convection Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 747 , 25 May 2014 , pp. 73 - 102
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer & large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503–537.Google Scholar
Bailon-Cuba, J., Emran, M. S. & Schumacher, J. 2010 Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 655, 152–173.Google Scholar
Bandi, M. M., Goldstein, W. I., Cressman, J. R. & Pumir, A. 2006 Energy flux fluctuations in a finite volume of turbulent flow. Phys. Rev. E 73, 026308.Google Scholar
Boffetta, G., De Lillo, F., Mazzino, A. & Musacchio, S. 2012 Bolgiano scale in confined Rayleigh–Taylor turbulence. J. Fluid Mech. 690, 426–440.Google Scholar
Calzavarini, E., Toschi, F. & Tripiccione, R. 2002 Evidences of Bolgiano scaling in 3D Rayleigh–Bénard convection. Phys. Rev. E 66, 016304.Google Scholar
Celani, A., Musacchio, S. & Vincenzi, D. 2010 Turbulence in more than two and less than three-dimensions. Phys. Rev. Lett. 104, 184506.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 1–25.Google Scholar
Ching, E. S. C. 2000 Intermittency of temperature field in turbulent convection. Phys. Rev. E 61, R33–R36.Google Scholar
Duchon, J. & Robert, R. 2000 Inertial energy dissipation for weak solutions of incompressible Euler and Navier–Stokes equations. Nonlinearity 13, 249–255.Google Scholar
Emran, M. & Schumacher, J. 2012 Conditional statistics of thermal dissipation rate in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 1–8.Google ScholarPubMed
Eyink, G. L. 2003 Local 4/5-law and energy dissipation anomaly in turbulence. Nonlinearity 16, 137–145.CrossRefGoogle Scholar
Funfschilling, D., Bodenschatz, E. & Ahlers, G. 2009 Search for the ‘ultimate state’ in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 103, 014503.CrossRefGoogle Scholar
Funfschilling, D., Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical samples with aspect ratio one and larger. J. Fluid Mech. 536, 145–154.Google Scholar
Grossmann, S. & Lohse, D. 2003 On geometry effects in Rayleigh–Bénard convection. J. Fluid Mech. 486, 105–114.CrossRefGoogle Scholar
Grötzbach, G. 1983 Spatial resolution requirements for direct numerical simulation of Rayleigh–Bénard convection. J. Comput. Phys. 49, 241–264.Google Scholar
He, X., Tong, P. & Ching, E. 2010 Statistics of the locally averaged thermal dissipation rate in turbulent Rayleigh–Bénard convection. J. Turbul. 11, 1–10.Google Scholar
Huang, S.-D., Kaczorowski, M., Ni, R. & Xia, K.-Q. 2013 Confinement induced heat transport enhancement in turbulent thermal convection. Phys. Rev. Lett. 111, 104501(1-5).Google Scholar
Kaczorowski, M. & Wagner, C. 2009 Analysis of the thermal plumes in turbulent Rayleigh–Bénard convection based on well-resolved numerical simulations. J. Fluid Mech. 618, 89–112.Google Scholar
Kaczorowski, M. & Xia, K.-Q. 2013 Turbulent flow in the bulk of Rayleigh–Bénard convection: small-scale properties in a cubic cell. J. Fluid Mech. 722, 596–617.Google Scholar
Kunnen, R. P. J., Clerx, H. J. H., Geurts, B. J., van Bokhoven, L. J. A., Akkermans, R. A. D. & Verzicco, R. 2008 Numerical and experimental investigation of structure-function scaling in turbulent Rayleigh–Bénard convection. Phys. Rev. E 77, 016302.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
Ni, R., Huang, S.-D. & Xia, K.-Q. 2011 Local energy dissipation rate balances local heat flux in the center of turbulent thermal convection. Phys. Rev. Lett. 107, 174503(1-5).Google Scholar
Niemela, J. J. & Sreenivasan, K. R. 2010 Does confined turbulent convection ever attain the ‘asymptotic scaling’ with 1/2 power? New J. Phys. 12, 115002.Google Scholar
Poel, E. P., Stevens, R. J. A. M., Sugiyama, K. & Lohse, D. 2012 Flow states in two-dimensional Rayleigh–Bénard convection as a function of aspect ratio and Rayleigh number. Phys. Fluids 24, 085104.Google Scholar
Qiu, X.-L. & Xia, K.-Q. 1998 Viscous boundary layers at the sidewall of a convection cell. Phys. Rev. E 58, 486–491.Google Scholar
Roche, P. E., Castaing, B., Chabaud, B. & Hebral, B. 2002 Prandtl and Rayleigh number dependences in Rayleigh–Bénard convection. Europhys. Lett. 58, 693–698.Google Scholar
Shang, X.-D., Qiu, X.-L., Tong, P. & Xia, K.-Q. 2004 Measurements of the local convective heat flux in turbulent Rayleigh–Bénard convection. Phys. Rev. E 70, 026308.Google Scholar
Shang, X.-D., Tong, P. & Xia, K.-Q. 2008 Scaling of the local convective heat flux in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 100, 244503.Google Scholar
Shang, X.-D. & Xia, K.-Q. 2001 Scaling of the velocity power spectra in turbulent thermal convection. Phys. Rev. E 64, 065301(R).Google Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and consequences for the required numerical resolution. New. J. Phys. 12, 075022.CrossRefGoogle Scholar
Shishkina, O. & Wagner, C. 2006 Analysis of thermal dissipation rates in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 546, 51–60.Google Scholar
Shishkina, O. & Wagner, C. 2007 Local heat flux in turbulent Rayleigh–Bénard convection. Phys. Fluids 19 (8), 085107-1–085107-13.Google Scholar
Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2010 Radial boundary layer structure and Nusselt number in Rayleigh–Bénard convection. J. Fluid Mech. 643, 495–507.Google Scholar
Sun, C., Ren, L.-Y., Song, H. & Xia, K.-Q. 2005a Heat transport by turbulent Rayleigh–Bénard convection in 1 m diameter cyindrical cells of widely varying aspect ratio. J. Fluid Mech. 542, 165–174.CrossRefGoogle Scholar
Sun, C., Xia, K.-Q. & Tong, P. 2005b Three-dimensional flow structures and dynamics of turbulent thermal convection in a cylindrical cell. Phys. Rev. E 72, 026302(13).Google Scholar
Sun, C., Zhou, Q. & Xia, K.-Q. 2006 Cascades of velocity and temperature fluctuations in buoyancy-driven thermal turbulence. Phys. Rev. Lett. 97, 144504.Google Scholar
Tao, B., Katz, J. & Meneveau, C. 2002 Statistical geometry of subgrid-scale stresses determined from holographic particle image velocimetry measurements. J. Fluid Mech. 457, 35–78.Google Scholar
Xia, K.-Q. 2013 Current trends and future directions in turbulent thermal convection. Theor. Appl. Mech. Lett. 3, 052001(1-12).CrossRefGoogle Scholar
Xin, Y.-B. & Xia, K.-Q. 1997 Boundary layer length scales in convective turbulence. Phys. Rev. E 56, 3010–3015.Google Scholar
Zhou, Q., Liu, B.-F., Li, C.-M. & Zhong, B.-C. 2012 Aspect ratio dependence of heat transport by turbulent Rayleigh–Bénard convection in rectangular cells. J. Fluid Mech. 710, 260–276.Google Scholar
Zhou, S.-Q. & Xia, K.-Q. 2001 Scaling properties of the temperature field in convective turbulence. Phys. Rev. Lett. 87, 064501.Google Scholar
Zhou, Q. & Xia, K.-Q. 2008 Comparative experimental study of local mixing of active and passive scalars in turbulent thermal convection. Phys. Rev. E 77, 056312.Google Scholar
Zhou, Q. & Xia, K.-Q. 2010 Universality of local dissipation scales in buoyancy-driven turbulence. Phys. Rev. Lett. 104, 124301.CrossRefGoogle ScholarPubMed

Kaczorowski et al. supplementary movie

The movie shows the temperature field (coded in colour; red: hot and blue cold) and velocity field (coded in the length of the arrows) in a vertical plane mid-way between the front and back walls, with $Ra=1\times10^9$, $Pr =4.38$ and $\Gamma = 1/8$.

Download Kaczorowski et al. supplementary movie(Video)
Video 61.1 MB