Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Soligo, Giovanni
Roccon, Alessio
and
Soldati, Alfredo
2019.
Breakage, coalescence and size distribution of surfactant-laden droplets in turbulent flow.
Journal of Fluid Mechanics,
Vol. 881,
Issue. ,
p.
244.
Song, Baofang
Plana, Carlos
Lopez, Jose M.
and
Avila, Marc
2019.
Phase-field simulation of core-annular pipe flow.
International Journal of Multiphase Flow,
Vol. 117,
Issue. ,
p.
14.
Roccon, Alessio
Zonta, Francesco
and
Soldati, Alfredo
2021.
Energy balance in lubricated drag-reduced turbulent channel flow.
Journal of Fluid Mechanics,
Vol. 911,
Issue. ,
Liu, Hao-Ran
Chong, Kai Leong
Wang, Qi
Ng, Chong Shen
Verzicco, Roberto
and
Lohse, Detlef
2021.
Two-layer thermally driven turbulence: mechanisms for interface breakup.
Journal of Fluid Mechanics,
Vol. 913,
Issue. ,
Plana, Carlos
Song, Baofang
and
Avila, Marc
2021.
Direct numerical simulation of two-phase pipe flow: Influence of the domain length on the flow regime.
International Journal of Multiphase Flow,
Vol. 144,
Issue. ,
p.
103786.
Liu, Hao-Ran
Ng, Chong Shen
Chong, Kai Leong
Lohse, Detlef
and
Verzicco, Roberto
2021.
An efficient phase-field method for turbulent multiphase flows.
Journal of Computational Physics,
Vol. 446,
Issue. ,
p.
110659.
Bochio, Gustavo
and
Rodriguez, Oscar M.H.
2022.
Modeling of laminar-turbulent stratified liquid–liquid flow with entrainment.
International Journal of Multiphase Flow,
Vol. 153,
Issue. ,
p.
104122.
Mangani, Francesca
Soligo, Giovanni
Roccon, Alessio
and
Soldati, Alfredo
2022.
Influence of density and viscosity on deformation, breakage, and coalescence of bubbles in turbulence.
Physical Review Fluids,
Vol. 7,
Issue. 5,
Warwaruk, Lucas
and
Ghaemi, Sina
2022.
Near-wall lubricating layer in drag-reduced flows of rigid polymers.
Physical Review Fluids,
Vol. 7,
Issue. 6,
Liu, Hao-Ran
Chong, Kai Leong
Yang, Rui
Verzicco, Roberto
and
Lohse, Detlef
2022.
Heat transfer in turbulent Rayleigh–Bénard convection through two immiscible fluid layers.
Journal of Fluid Mechanics,
Vol. 938,
Issue. ,
Popescu, E.-R.
Dawson, J.R.
Brandt, L.
Colin, C.
and
Tanguy, S.
2022.
Interaction between the turbulent boundary layer flow of superheated vapor and the velocity field induced by liquid vaporization.
International Journal of Heat and Fluid Flow,
Vol. 97,
Issue. ,
p.
109033.
Hori, Naoki
Ng, Chong Shen
Lohse, Detlef
and
Verzicco, Roberto
2023.
Interfacial-dominated torque response in liquid–liquid Taylor–Couette flows.
Journal of Fluid Mechanics,
Vol. 956,
Issue. ,
Giamagas, Georgios
Zonta, Francesco
Roccon, Alessio
and
Soldati, Alfredo
2023.
Propagation of capillary waves in two-layer oil–water turbulent flow.
Journal of Fluid Mechanics,
Vol. 960,
Issue. ,
Roccon, Alessio
Zonta, Francesco
and
Soldati, Alfredo
2023.
Phase-field modeling of complex interface dynamics in drop-laden turbulence.
Physical Review Fluids,
Vol. 8,
Issue. 9,
Zhu, Jingfang
Tang, Xubing
Jia, Haiyang
Han, Longxiang
Lin, Cunguo
Zhang, Jinwei
and
Li, Longyang
2024.
Influence of wettability on drag reduction performance during turbulent flow.
Physics of Fluids,
Vol. 36,
Issue. 10,
Roccon, Alessio
Zonta, Francesco
and
Soldati, Alfredo
2024.
Turbulent drag reduction in water-lubricated channel flow of highly viscous oil.
Physical Review Fluids,
Vol. 9,
Issue. 5,
Giamagas, Georgios
Zonta, Francesco
Roccon, Alessio
and
Soldati, Alfredo
2024.
Turbulence and Interface Waves in Stratified Oil–Water Channel Flow at Large Viscosity Ratio.
Flow, Turbulence and Combustion,
Vol. 112,
Issue. 1,
p.
15.
Li, Botong
Zhao, Zitian
Meng, Linyu
and
Zhu, Liangliang
2024.
On the fluid drag reduction in scallop surface.
The European Physical Journal E,
Vol. 47,
Issue. 6,
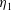 $\unicode[STIX]{x1D702}_{1}$) from a main layer of a more-viscous fluid (viscosity
$\unicode[STIX]{x1D702}_{1}$) from a main layer of a more-viscous fluid (viscosity 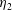 $\unicode[STIX]{x1D702}_{2}$). To single out the effect of surface tension, we focus initially on two fluids having the same density and the same viscosity (
$\unicode[STIX]{x1D702}_{2}$). To single out the effect of surface tension, we focus initially on two fluids having the same density and the same viscosity (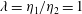 $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D702}_{1}/\unicode[STIX]{x1D702}_{2}=1$), and we lower the viscosity of the lubricating layer down to
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D702}_{1}/\unicode[STIX]{x1D702}_{2}=1$), and we lower the viscosity of the lubricating layer down to 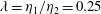 $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D702}_{1}/\unicode[STIX]{x1D702}_{2}=0.25$, which corresponds to a physically realizable experimental set-up consisting of light oil and water. A database comprising original direct numerical simulations of two-phase flow channel turbulence is used to study the physical mechanisms driving drag reduction, which we report between 20 and 30 percent. The maximum drag reduction occurs when the two fluids have the same viscosity (
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D702}_{1}/\unicode[STIX]{x1D702}_{2}=0.25$, which corresponds to a physically realizable experimental set-up consisting of light oil and water. A database comprising original direct numerical simulations of two-phase flow channel turbulence is used to study the physical mechanisms driving drag reduction, which we report between 20 and 30 percent. The maximum drag reduction occurs when the two fluids have the same viscosity (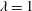 $\unicode[STIX]{x1D706}=1$), and corresponds to the relaminarization of the lubricating layer. Decreasing the viscosity of the lubricating layer (
$\unicode[STIX]{x1D706}=1$), and corresponds to the relaminarization of the lubricating layer. Decreasing the viscosity of the lubricating layer (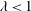 $\unicode[STIX]{x1D706}<1$) induces a marginally decreased drag reduction, but also helps sustaining strong turbulence in the lubricating layer. This led us to infer two different mechanisms for the two drag-reduced systems, each of which is ultimately controlled by the outcome of the competition between viscous, inertial and surface tension forces.
$\unicode[STIX]{x1D706}<1$) induces a marginally decreased drag reduction, but also helps sustaining strong turbulence in the lubricating layer. This led us to infer two different mechanisms for the two drag-reduced systems, each of which is ultimately controlled by the outcome of the competition between viscous, inertial and surface tension forces.

