Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T13:49:10.443Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent 2.5-dimensional dynamos

Published online by Cambridge University Press:  22 June 2016

K. Seshasayanan Open the ORCID record for K. Seshasayanan [Opens in a new window]  and
A. Alexakis
K. Seshasayanan*
Affiliation:
Laboratoire de Physique Statistique, École Normale Supérieure, PSL Research University; Université Paris Diderot Sorbonne Paris-Cité; Sorbonne Universités UPMC Univ Paris 06; CNRS; 24 rue Lhomond, 75005 Paris, France
A. Alexakis
Affiliation:
Laboratoire de Physique Statistique, École Normale Supérieure, PSL Research University; Université Paris Diderot Sorbonne Paris-Cité; Sorbonne Universités UPMC Univ Paris 06; CNRS; 24 rue Lhomond, 75005 Paris, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the linear stage of the dynamo instability of a turbulent two-dimensional flow with three components 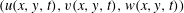$(u(x,y,t),v(x,y,t),w(x,y,t))$ that is sometimes referred to as a 2.5-dimensional (2.5-D) flow. The flow evolves based on the two-dimensional Navier–Stokes equations in the presence of a large-scale drag force that leads to the steady state of a turbulent inverse cascade. These flows provide an approximation to very fast rotating flows often observed in nature. The low dimensionality of the system allows for the realization of a large number of numerical simulations and thus the investigation of a wide range of fluid Reynolds numbers 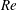$Re$, magnetic Reynolds numbers 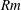$Rm$ and forcing length scales. This allows for the examination of dynamo properties at different limits that cannot be achieved with three-dimensional simulations. We examine dynamos for both large and small magnetic Prandtl-number turbulent flows 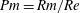$Pm=Rm/Re$, close to and away from the dynamo onset, as well as dynamos in the presence of scale separation. In particular, we determine the properties of the dynamo onset as a function of 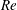$Re$ and the asymptotic behaviour in the large 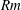$Rm$ limit. We are thus able to give a complete description of the dynamo properties of these turbulent 2.5-D flows.

JFM classification

MHD and Electrohydrodynamics: Dynamo theory MHD and Electrohydrodynamics: MHD and Electrohydrodynamics Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 799 , 25 July 2016 , pp. 246 - 264
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexakis, A. 2015 Rotating Taylor–Green Flow. J. Fluid Mech. 769, 46–78.Google Scholar
Alexakis, A. & Doering, C. R. 2006 Energy and enstrophy dissipation in steady state 2d turbulence. Phys. Lett. A 359, 652–657.Google Scholar
Baqui, Y. B. & Davidson, P. A. 2015 A phenomenological theory of rotating turbulence. Phys. Fluids 27 (2), 025107.Google Scholar
Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5 (01), 113–133.Google Scholar
Boffetta, G. 2007 Energy and enstrophy fluxes in the double cascade of two-dimensional turbulence. J. Fluid Mech. 589, 253–260.CrossRefGoogle Scholar
Boffetta, G. & Ecke, R. E. 2012 Two-dimensional turbulence. Annu. Rev. Fluid Mech. 44, 427–451.Google Scholar
van Bokhoven, L. J. A., Clercx, H. J. H., van Heijst, G. J. F. & Trieling, R. R. 2009 Experiments on rapidly rotating turbulent flows. Phys. Fluids 21 (9), 096601.CrossRefGoogle Scholar
Brandenburg, A. 2009 Advances in theory and simulations of large-scale dynamos. Space Sci. Rev. 144 (1–4), 87–104.Google Scholar
Brandenburg, A., Rädler, K.-H. & Schrinner, M. 2008 Scale dependence of alpha effect and turbulent diffusivity. Astron. Astrophys. 482, 739–746.Google Scholar
Calkins, M. A., Julien, K., Tobias, S. M. & Aurnou, J. M. 2015 A multiscale dynamo model driven by quasi-geostrophic convection. J. Fluid Mech. 780, 143–166.Google Scholar
Calkins, M. A., Julien, K., Tobias, S. M., Aurnou, J. M. & Marti, P. 2016 Convection-driven kinematic dynamos at low Rossby and magnetic Prandtl numbers: single mode solutions. Phys. Rev. E 93, 023115.Google Scholar
Campagne, A., Gallet, B., Moisy, F. & Cortet, P.-P. 2014 Direct and inverse energy cascades in a forced rotating turbulence experiment. Phys. Fluids 26 (12), 125112.Google Scholar
Cattaneo, F. & Tobias, S. M. 2014 On large-scale dynamo action at high magnetic Reynolds number. Astrophys. J. 789, 70.Google Scholar
Chen, Q., Chen, S., Eyink, G. L. & Holm, D. D. 2005 Resonant interactions in rotating homogeneous three-dimensional turbulence. J. Fluid Mech. 542, 139–164.Google Scholar
Chertkov, M., Connaughton, C., Kolokolov, I. & Lebedev, V. 2007 Dynamics of energy condensation in two-dimensional turbulence. Phys. Rev. Lett. 99 (8), 084501.Google Scholar
Childress, S. 1969 A class of solutions of the magnetohydrodynamic dynamo problem. In The Application of Modern Physics to the Earth and Planetary Interiors, pp. 629–648. Wiley.Google Scholar
Constantin, P., Foias, C. & Manley, O. P. 1994 Effects of the forcing function spectrum on the energy spectrum in 2-D turbulence. Phys. Fluids 6, 427–429.Google Scholar
Courvoisier, A., Hughes, D. W. & Tobias, S. M. 2006 𝛼 effect in a family of chaotic flows. Phys. Rev. Lett. 96 (3), 034503.Google Scholar
Davidson, P. A. 2014 The dynamics and scaling laws of planetary dynamos driven by inertial waves. Geophys. J. Intl 198 (3), 1832–1847.CrossRefGoogle Scholar
Deusebio, E., Boffetta, G., Lindborg, E. & Musacchio, S. 2014 Dimensional transition in rotating turbulence. Phys. Rev. E 90 (2), 023005.Google Scholar
Ekman, V. W. 1905 On the influence of the earth∖’s rotation on ocean currents. Ark. Mat. Astron. Fys. 2, 1–53.Google Scholar
Eyink, G. L. 1996 Exact results on stationary turbulence in 2D: consequences of vorticity conservation. Physica D 91, 97–142.Google Scholar
Gallet, B. 2015 Exact two-dimensionalization of rapidly rotating large-Reynolds-number flows. J. Fluid Mech. 783, 412–447.Google Scholar
Gallet, B., Campagne, A., Cortet, P.-P. & Moisy, F. 2014 Scale-dependent cyclone-anticyclone asymmetry in a forced rotating turbulence experiment. Phys. Fluids 26 (3), 035108.Google Scholar
Galloway, D. J. & Proctor, M. R. E. 1992 Numerical calculations of fast dynamos in smooth velocity fields with realistic diffusion. Nature 356, 691–693.Google Scholar
Gilbert, A. D. 2003 Dynamo theory. In Handbook of Mathematical Fluid Dynamics, vol. 2, pp. 355–441. Elsevier.CrossRefGoogle Scholar
Gomez, D. O., Mininni, P. D. & Dmitruk, P. 2005 Parallel simulations in turbulent mhd. Phys. Scr. T116, 123.CrossRefGoogle Scholar
Herreman, W. & Lesaffre, P. 2011 Stokes drift dynamos. J. Fluid Mech. 679, 32–57.Google Scholar
Hopfinger, E. J. & van Heijst, G. J. F. 1993 Vortices in rotating fluids. Annu. Rev. Fluid Mech. 25, 241–289.Google Scholar
Hossain, M. 1994 Reduction in the dimensionality of turbulence due to a strong rotation. Phys. Fluids 6, 1077–1080.Google Scholar
Hough, S. S. 1897 On the application of harmonic analysis to the dynamical theory of the tides. Part I. On Laplace’s ‘oscillations of the first species, and on the dynamics of ocean currents. Phil. Trans. R. Soc. Lond. A 189, 201–257.Google Scholar
Iskakov, A. B., Schekochihin, A. A., Cowley, S. C., McWilliams, J. C. & Proctor, M. R. E. 2007 Numerical demonstration of fluctuation dynamo at low magnetic prandtl numbers. Phys. Rev. Lett. 98 (20), 208501.Google Scholar
Izakov, M. N. 2013 Large-scale quasi-two-dimensional turbulence and a inverse spectral flux of energy in the atmosphere of Venus. Solar Syst. Res. 47, 170–181.Google Scholar
Kraichnan, R. H.1967 Inertial ranges in two-dimensional turbulence. Tech. Rep. DTIC Document.Google Scholar
Krause, F. & Raedler, K.-H. 1980 Mean-field Magnetohydrodynamics and Dynamo Theory. Pergamon.Google Scholar
Lanotte, A., Noullez, A., Vergassola, M. & Wirth, A. 1999 Large-scale dynamo produced by negative magnetic eddy diffusivities. Geophys. Astrophys. Fluid Dyn. 91 (1–2), 131–146.Google Scholar
Laurie, J., Boffetta, G., Falkovich, G., Kolokolov, I. & Lebedev, V. 2014 Universal profile of the vortex condensate in two-dimensional turbulence. Phys. Rev. Lett. 113, 254503.Google Scholar
Mininni, P. D. 2007 Inverse cascades and 𝛼 effect at a low magnetic Prandtl number. Phys. Rev. E 76 (2), 026316.Google Scholar
Mininni, P. D. & Pouquet, A. 2010 Rotating helical turbulence. I. Global evolution and spectral behavior. Phys. Fluids 22 (3), 035105.Google Scholar
Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Nazarenko, S. V. & Schekochihin, A. A. 2011 Critical balance in magnetohydrodynamic, rotating and stratified turbulence: towards a universal scaling conjecture. J. Fluid Mech. 677, 134–153.Google Scholar
Otani, N. F. 1993 A fast kinematic dynamo in two-dimensional time-dependent flows. J. Fluid Mech. 253, 327–340.Google Scholar
Parker, E. N. 1955 Hydromagnetic dynamo models. Astrophys. J. 122, 293.Google Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics. Springer.Google Scholar
Pierrehumbert, R. T, Held, I. M & Swanson, K. L 1994 Spectra of local and nonlocal two-dimensional turbulence. Chaos, Solitons Fractals 4 (6), 1111–1116.Google Scholar
Plunian, F. & Rädler, K.-H. 2002 Subharmonic dynamo action in the Roberts Flow. Geophys. Astrophys. Fluid Dyn. 96, 115–133.Google Scholar
Ponomarenko, Yu. B. 1973 On the theory of the hydrodynamic dynamo. J. Appl. Mech. Tech. Phys. 14, 775–779.Google Scholar
Ponty, Y., Mininni, P. D., Montgomery, D. C., Pinton, J.-F., Politano, H. & Pouquet, A. 2005 Numerical study of dynamo action at low magnetic Prandtl numbers. Phys. Rev. Lett. 94 (16), 164502.Google Scholar
Proctor, M. R. E. & Gilbert, A. D. 1995 Lectures on Solar and Planetary Dynamos. Cambridge University Press.Google Scholar
Proudman, J. 1916 On the motion of solids in a liquid possessing vorticity. Phil. Trans. R. Soc. Lond. A 92, 408–424.Google Scholar
Rädler, K.-H. & Brandenburg, A. 2009 Mean-field effects in the galloway–proctor flow. Mon. Not. R. Astron. Soc. 393 (1), 113–125.Google Scholar
Roberts, G. O. 1972 Dynamo action of fluid motions with two-dimensional periodicity. Phil. Trans. R. Soc. Lond. A 271 (1216), 411–454.Google Scholar
Scott, J. F. 2014 Wave turbulence in a rotating channel. J. Fluid Mech. 741, 316–349.Google Scholar
Sen, A., Mininni, P. D., Rosenberg, D. & Pouquet, A. 2012 Anisotropy and nonuniversality in scaling laws of the large-scale energy spectrum in rotating turbulence. Phys. Rev. E 86 (3), 036319.Google Scholar
Smith, L. M. & Waleffe, F. 1999 Transfer of energy to two-dimensional large scales in forced, rotating three-dimensional turbulence. Phys. Fluids 11, 1608–1622.Google Scholar
Smith, S. G. L. & Tobias, S. M. 2004 Vortex dynamos. J. Fluid Mech. 498, 1–21.CrossRefGoogle Scholar
Sous, D., Sommeria, J. & Boyer, D. L. 2013 Friction law and turbulent properties in a laboratory Ekman boundary layer. Phys. Fluids 25 (4), 046602.CrossRefGoogle Scholar
Staplehurst, P. J., Davidson, P. A. & Dalziel, S. B. 2008 Structure formation in homogeneous freely decaying rotating turbulence. J. Fluid Mech. 598, 81–105.Google Scholar
Sugihara, Y., Migita, M. & Honji, H. 2005 Orderly flow structures in grid-generated turbulence with background rotation. Fluid Dyn. Res. 36, 23–34.Google Scholar
Taylor, G. I. 1917 Motion of solids in fluids when the flow is not irrotational. Proc. R. Soc. London A 93, 99–113.Google Scholar
Thiele, M. & Müller, W.-C. 2009 Structure and decay of rotating homogeneous turbulence. J. Fluid Mech. 637, 425.CrossRefGoogle Scholar
Tobias, S. M. & Cattaneo, F. 2008a Dynamo action in complex flows: the quick and the fast. J. Fluid Mech. 601, 101–122.Google Scholar
Tobias, S. M. & Cattaneo, F. 2008b Limited role of spectra in dynamo theory: coherent versus random dynamos. Phys. Rev. Lett. 101, 125003.Google Scholar
Tobias, S. M. & Cattaneo, F. 2013 Shear-driven dynamo waves at high magnetic Reynolds number. Nature 497 (7450), 463–465.Google Scholar
Tobias, S. M. & Cattaneo, F. 2015 The electromotive force in multi-scale flows at high magnetic Reynolds number. J. Plasma Phys. 81 (6), 395810601.Google Scholar
Vishik, M. M. 1989 Magnetic field generation by the motion of a highly conducting fluid. Geophys. Astrophys. Fluid Dynam. 48, 151–167.Google Scholar
Waleffe, F. 1993 Inertial transfers in the helical decomposition. Phys. Fluids 5, 677–685.Google Scholar
Yarom, E., Vardi, Y. & Sharon, E. 2013 Experimental quantification of inverse energy cascade in deep rotating turbulence. Phys. Fluids 25 (8), 085105.Google Scholar
Yeung, P. K. & Zhou, Y. 1998 Numerical study of rotating turbulence with external forcing. Phys. Fluids 10, 2895–2909.Google Scholar
Yoshimatsu, K., Midorikawa, M. & Kaneda, Y. 2011 Columnar eddy formation in freely decaying homogeneous rotating turbulence. J. Fluid Mech. 677, 154–178.Google Scholar
Zel’dovich, Ya. B. 1958 Electromagnetic interaction with parity violation. Sov. Phys. JETP 6, 1184; (Zh. Eksp. Teor. Fiz. 33, 1531 (1957)).Google Scholar