Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-27T18:45:46.741Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulence statistics in smooth wall oscillatory boundary layer flow

Published online by Cambridge University Press:  18 June 2018

Dominic A. van der A Open the ORCID record for Dominic A. van der A [Opens in a new window] ,
Pietro Scandura  and
Tom O’Donoghue
Dominic A. van der A*
Affiliation:
School of Engineering, University of Aberdeen, Aberdeen, AB24 3UE, UK
Pietro Scandura
Affiliation:
Department of Civil Engineering and Architecture, University of Catania, Via Santa Sofia, 64 95123, Catania, Italy
Tom O’Donoghue
Affiliation:
School of Engineering, University of Aberdeen, Aberdeen, AB24 3UE, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Turbulence characteristics of an asymmetric oscillatory boundary layer flow are analysed through two-component laser-Doppler measurements carried out in a large oscillatory flow tunnel and direct numerical simulation (DNS). Five different Reynolds numbers, 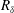$R_{\unicode[STIX]{x1D6FF}}$, in the range 846–2057 have been investigated experimentally, where 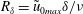$R_{\unicode[STIX]{x1D6FF}}=\tilde{u} _{0max}\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D708}$ with 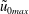$\tilde{u} _{0max}$ the maximum oscillatory velocity in the irrotational region, 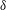$\unicode[STIX]{x1D6FF}$ the Stokes length and $\unicode[STIX]{x1D708}$ the fluid kinematic viscosity. DNS has been carried out for the lowest three 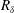$R_{\unicode[STIX]{x1D6FF}}$ equal to 846, 1155 and 1475. Both experimental and numerical results show that the flow statistics increase during accelerating phases of the flow and especially at times of transition to turbulent flow. Once turbulence is fully developed, the near-wall statistics remain almost constant until the late half-cycle, with values close to those reported for steady wall-bounded flows. The higher-order statistics reach large values within a normalized wall distance of approximately 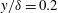$y/\unicode[STIX]{x1D6FF}=0.2$ at phases corresponding to the onset of low-speed streak breaking, because of the intermittency of the velocity fluctuations at these times. In particular, the flatness of the streamwise velocity fluctuations reaches values of the order of ten, while the flatness of the wall-normal velocity fluctuations reaches values of several hundreds. Far from the wall, at locations where the vertical gradient of the streamwise velocity is zero, the skewness is approximately zero and the flatness is approximately equal to 3, representative of a normal distribution. At lower elevations the distribution of the fluctuations deviate substantially from a normal distribution, but are found to be well described by other standard theoretical probability distributions.

JFM classification

Geophysical and Geological Flows: Coastal engineering Waves/Free-surface Flows: Surface gravity waves Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 849 , 25 August 2018 , pp. 192 - 230
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

van der A, D. A., O’Donoghue, T., Davies, A. G. & Ribberink, J. S. 2011 Experimental study of the turbulent boundary layer in acceleration-skewed oscillatory flow. J. Fluid Mech. 684, 251–283.Google Scholar
Abreu, T., Silva, P. A., Sancho, F. & Temperville, A. 2010 Analytical approximate wave form for asymmetric waves. Coast. Engng 57, 656–667.Google Scholar
Alfredsson, P. H., Johansson, A. V., Haritonidis, J. H. & Eckelmann, H. 1988 The fluctuating wall-shear stress and the velocity field in the viscous sublayer. Phys. Fluids 31 (5), 1026–1033.Google Scholar
Barlow, R. S. & Johnston, J. P. 1985 Structure of turbulent boundary layers on a concave surface. J. Fluid Mech. 191, 137–176.Google Scholar
Blondeaux, P. & Vittori, G. 1994 Wall imperfections as a triggering mechanism for Stokes-layer transition. J. Fluid Mech. 264, 107–135.Google Scholar
Buchhave, P., George, W. K. & Lumley, J. L. 1979 The measurement of turbulence with the laser-Doppler anemometer. Annu. Rev. Fluid Mech. 11, 443–503.Google Scholar
Carstensen, S., Sumer, B. M. & Fredsøe, J. 2010 Coherent structures in wave boundary layers. Part 1. Oscillatory motion. J. Fluid Mech. 646, 169–206.Google Scholar
Cheng, Z., Chauchat, J., Hsu, T.-J. & Calantoni, J. 2018 Eddy interaction model for turbulent suspension in Reynolds-averaged Euler–Lagrange simulations of steady sheet flow. Adv. Water Resour. 111, 435–451.Google Scholar
Costamagna, P., Vittori, G. & Blondeaux, P. 2003 Coherent structures in oscillatory boundary layers. J. Fluid Mech. 474, 1–33.Google Scholar
Durst, F., Jovanovic, J. & Sender, J. 1995 LDA measurements in the near-wall region of turbulent pipe flow. J. Fluid Mech. 295, 305–335.Google Scholar
Durst, F., Müller, R. & Jovanovic, J. 1988 Determination of the measuring position in laser-Doppler anemometry. Exp. Fluids 6, 105–110.Google Scholar
Gonzalez-Rodriguez, D. & Madsen, O. S. 2011 Boundary-layer hydrodynamics and bedload sediment transport in oscillating water tunnels. J. Fluid Mech. 667, 48–84.Google Scholar
Hino, M., Kashiwayanagi, M., Nakayama, A. & Hara, T. 1983 Experiments on the turbulent statistics and the structure of a reciprocating oscillatory flow. J. Fluid Mech. 131, 363–400.Google Scholar
Hino, M., Sawamoto, M. & Takasu, S. 1976 Experiments on transition to turbulence in an oscillatory pipe flow. J. Fluid Mech. 75 (2), 193–207.Google Scholar
Hofland, B. & Battjes, J. A. 2006 Probability density function of instantaneous drag forces and shear stresses on a bed. J. Hydraul. Engng ASCE 132 (11), 1169–1175.Google Scholar
Jensen, B. L., Sumer, B. M. & Fredsøe, J. 1989 Turbulent oscillatory boundary layers at high Reynolds numbers. J. Fluid Mech. 206, 265–297.Google Scholar
Johnson, N. L., Kotz, S. & Balakrishnan, N. 1994 Continuous Univariate Distributions. Wiley.Google Scholar
Jonsson, I. G. & Carlsen, N. A. 1976 Experimental and theoretical investigations in an oscillatory turbulent boundary layer. J. Hydraul. Res. 14, 45–60.Google Scholar
Jovanovic, J., Durst, F. & Johansson, T. G. 1993 Statistical analysis of the dynamic equations for higher-order moments in turbulent wall bounded flow. Phys. Fluids 5 (11), 2886–2900.Google Scholar
Karlsson, R. I. & Johansson, T. G. 1986 LDV measurements of higher-order moments of velocity fluctuations in a boundary layer. In Laser Anemometry in Fluid Mechanics III (ed. Adrian, R. J.), pp. 273–289. Ladoan – Instituto Superior Tecnico, Lisbon.Google Scholar
Kim, J., Parviz, M. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kreplin, H. & Eckelmann, H. 1979 Behaviour of the three fluctuating velocity components in the wall region of a turbulent channel flow. Phys. Fluids 22 (7), 1233–1239.Google Scholar
Mazzuoli, M., Vittori, G. & Blondeaux, P. 2011 Turbulent spots in oscillatory boundary layers. J. Fluid Mech. 685, 365–376.Google Scholar
Ozdemir, C. E., Hsu, T.-J. & Balachandar, S. 2014 Direct numerical simulations of transition and turbulence in smooth-walled Stokes boundary layer. Phys. Fluids 26, 045108.Google Scholar
Pedocchi, F., Cantero, M. I. & Garcia, M. H. 2011 Turbulent kinetic energy balance of an oscillatory boundary layer in the transition to the fully turbulent regime. J. Turbul. 12 (32), 1–27.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Salon, S., Armenio, V. & Crise, A. 2007 A numerical investigation of the Stokes boundary layer in the turbulent regime. J. Fluid Mech. 570, 253–296.Google Scholar
Scandura, P. 2007 Steady streaming in a turbulent oscillating boundary layer. J. Fluid Mech. 571, 265–280.Google Scholar
Scandura, P. 2013 Two dimensional vortex structures in the bottom boundary layer of progressive and solitary waves. J. Fluid Mech. 728, 340–361.Google Scholar
Scandura, P., Faraci, C. & Foti, E. 2016 A numerical investigation of acceleration-skewed oscillatory flows. J. Fluid Mech. 808, 576–613.Google Scholar
Shi, H. & Yu, X. 2015 An effective Euler–Lagrange model for suspended sediment transport by open channel flows. Intl J. Sedim. Res. 30 (4), 361–370.Google Scholar
Sleath, J. F. A. 1987 Turbulent oscillatory flow over rough beds. J. Fluid Mech. 182, 369–409.Google Scholar
Spalart, P. R. & Baldwin, B. S. 1989 Direct simulation of a turbulent oscillating boundary layer. In 6th Symposium on Turbulent Shear Flows (ed. Durst, F., Launder, B., Schmidt, F. & Whitelaw, J.), pp. 417–440. Springer.Google Scholar
Tsinober, A. 2009 An Informal Conceptual Introduction to Turbulence, 2nd edn. Fluid Mechanics and its Applications, vol. 92. Springer.Google Scholar
Vittori, G. & Verzicco, R. 1998 Direct simulation of transition in an oscillatory boundary layer. J. Fluid Mech. 371, 207–232.Google Scholar
Wallace, J. M. 2016 Quadrant analysis in turbulence research: history and evolution. Annu. Rev. Fluid Mech. 48, 131–158.Google Scholar
Wei, T. & Willmarth, W. W. 1989 Reynolds-number effects on the structure of a turbulent channel flow. J. Fluid Mech. 204, 57–95.Google Scholar
Wu, F. & Yang, K. 2004 Entrainment probabilities of mixed-size sediment incorporating near-bed coherent flow structures. J. Hydraul. Engng ASCE 130 (12), 1187–1197.Google Scholar
Yuan, J. & Madsen, O. S. 2014 Experimental study of turbulent oscillatory boundary layers in an oscillating water tunnel. Coast. Engng 89, 63–84.Google Scholar