Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-25T08:01:52.399Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulence intensity in wall-bounded and wall-free flows

Published online by Cambridge University Press:  31 March 2015

Ian P. Castro
Ian P. Castro*
Affiliation:
Aeronautics and Astronautics, Faculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Turbulence intensity variations in the outer region of turbulent shear flows are considered, in the context of the diagnostic plot first introduced by Alfredsson et al. (Phys. Fluids, vol. 23, 2011, 041702) and for both (smooth and rough) wall-bounded flows and classical free shear flows. With 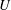$U$ defined as the mean velocity within the flow, 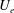$U_{e}$ as a suitable reference velocity and 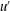$u^{\prime }$ as the root mean square of the fluctuating velocity, it is demonstrated that, for wall flows, the attached eddy hypothesis yields a closely linear diagnostic plot (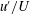$u^{\prime }/U$ versus 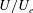$U/U_{e}$) over a certain Reynolds number range, explaining why the relation seems to work well for both boundary layers and channels despite its lack of any physical basis (Castro et al., J. Fluid Mech., vol. 727, 2013, pp. 119–131). It is shown that mixing layers, jets and wakes also exhibit linear variations of 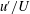$u^{\prime }/U$ versus 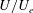$U/U_{e}$ over much of the flows (starting roughly from where the turbulence production is a maximum), with slopes of these variations determined by the total mean strain rate, characterised by Townsend’s flow constant 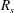$R_{s}$. The diagnostic plot thus has a wider range of applicability than might have been anticipated.

JFM classification

Turbulent Flows: Shear layer turbulence Turbulent Flows: Turbulent boundary layers Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 770 , 10 May 2015 , pp. 289 - 304
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alfredsson, P. H. & Örlü, R. 2010 The diagnostic plot – a litmus test for wall bounded turbulence data. Eur. J. Mech. (B/Fluids) 29, 403–406.Google Scholar
Alfredsson, P. H., Örlü, R. & Segalini, A. 2012 A new formulation for the streamwise turbulence intensity distribution in wall-bounded turbulent flows. Eur. J. Mech. (B/Fluids) 36, 167–175.Google Scholar
Alfredsson, P. H., Segalini, A. & Örlü, R. 2011 A new scaling for the streamwise turbulence intensity in wall-bounded turbulent flows and what it tells us about the outer peak. Phys. Fluids 23, 041702.Google Scholar
Amir, M. & Castro, I. P. 2011 Turbulence in rough-wall boundary layers: universality issues. Exp. Fluids 51, 313–326.Google Scholar
Bell, J. H. & Mehta, R. D. 1990 Development of a two-stream mixing layer from tripped to untripped boundary layers. AIAA J. 28, 2034–2042.Google Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to $\mathit{Re}_{{\it\tau}}=4000$ . J. Fluid Mech. 742, 171–191.CrossRefGoogle Scholar
Birch, D. M. & Morrison, J. J. 2011 Similarity of the streamwise velocity component in very-rough-wall channel flow. J. Fluid Mech. 668, 174–201.Google Scholar
Cant, R., Castro, I. P. & Walklate, P. 2002 Plane jets impinging on porous walls. Exp. Fluids 32, 16–26.Google Scholar
Castro, I. P. & Bradshaw, P. 1976 The turbulence structure of a highly curved mixing layer. J. Fluid Mech. 73, 265–304.Google Scholar
Castro, I. P. & Epik, E. 1998 Boundary layer development after a separated region. J. Fluid Mech. 374, 91–116.Google Scholar
Castro, I. P., Segalini, A. & Alfredsson, P. H. 2013 Outer layer turbulence intensities in smooth- and rough-wall boundary layers. J. Fluid Mech. 727, 119–131.Google Scholar
Champagne, F. H., Pao, Y. H. & Wygnanski, I. J. 1976 On the two-dimensional mixing region. J. Fluid Mech. 74, 209–250.CrossRefGoogle Scholar
Chauhan, K. A., Monkwitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41, 1–23.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $\mathit{Re}_{{\it\tau}}=2003$ . Phys. Fluids 18, 011702.CrossRefGoogle Scholar
Hussain, H. J., Capp, S. P. & George, W. K. 1994 Velocity measurements in a high-Reynolds-number momentum-conserving, axisymmetric, turbulent jet. J. Fluid Mech. 258, 31–75.Google Scholar
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. P. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Meteorol. 145, 276–306.Google Scholar
Hutchins, N., Monty, J. P., Ganapathisubramani, B., Ng, H. C. G. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.CrossRefGoogle Scholar
Inoue, M. & Pullin, D. I. 2011 Large-eddy simulation of the zero-pressure-gradient turbulent boundary layer up to $\mathit{Re}_{{\it\theta}}=O(10^{12})$ . J. Fluid Mech. 686, 507–533.CrossRefGoogle Scholar
Krogstad, P.-Ȧ. & Efros, V. 2012 About turbulence statistics in the outer part of a boundary layer developing over 2D surface roughness. Phys. Fluids 24, 075112.Google Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Effect of the computational domain on direct simulations of turbulent channels up to $\mathit{Re}_{{\it\tau}}=4200$ . Phys. Fluids 26, 011702.CrossRefGoogle Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. R3, 1–11.Google Scholar
Marusic, I., Uddin, A. K. M. & Perry, A. E. 1997 Similarity law for the streamwise turbulence intensity in zero-pressure-gradient turbulent boundary layers. Phys. Fluids 9, 3718–3726.Google Scholar
Metzger, M., McKeon, B. J. & Holmes, H. 2007 The near-neutral atmospheric surface layer: turbulence and non-stationarity. Phil. Trans. R. Soc. Lond. A 365, 859–876.Google Scholar
Monkewitz, P. A., Chauhan, K. A. & Nagib, H. M. 2007 Self-consistent high-Reynolds-number asymptotics for zero-pressure-gradient turbulent boundary layers. Phys. Fluids 19, 115101.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to $\mathit{Re}_{{\it\tau}}=590$ . Phys. Fluids 11, 943–945.CrossRefGoogle Scholar
Nagib, H. M., Christophorou, C. & Monkewitz, P. A. 2004 High Reynolds number turbulent boundary layers subjected to various pressure gradient conditions. In IUTAM Symposium on One Hundred Years of Boundary Layer Research. DLR Göttingen, Germany (ed. Meier, G. & Sreenivasan, K.). Springer,Google Scholar
Oweis, G. F., Winkel, E. S., Cutbrith, J. M., Ceccio, S. L., Perlin, M. & Dowling, D. R. 2010 The mean velocity profile of a smooth-flat-plate turbulent boundary layer at high Reynolds number. J. Fluid Mech. 665, 357–381.Google Scholar
Pullin, D. I., Inoue, M. & Salto, N. 2013 On the asymptotic state of high Reynolds number, smooth-wall turbulent flows. Phys. Fluids 25, 015116.Google Scholar
Redford, J. A., Castro, I. P. & Coleman, G. N. 2012 On the universality of turbulent axisymmetric wakes. J. Fluid Mech. 710, 419–452.Google Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of diret numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.Google Scholar
Schlichting, H. 1968 Boundary Layer Theory, 6th edn. McGraw-Hill.Google Scholar
Schultz, M. P. & Flack, K. A. 2013 Reynolds-number scaling of turbulent channel flow. Phys. Fluids 25, 025104.CrossRefGoogle Scholar
Skȧre, P. E. & Krogstad, P.-Ȧ. 1994 A turbulent equilibrium boundary layer near separation. J. Fluid Mech. 272, 319–348.CrossRefGoogle Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Webb, S. & Castro, I. P. 2006 Axisymmetric jets impinging on porous walls. Exp. Fluids 40, 951–961.Google Scholar
Winkel, E. S., Cutbirth, J. M., Ceccio, S. L., Perlin, M. & Dowling, D. R. 2012 Turbulence profiles from a smooth flat-plate turbulent boundary layer at high Reynolds number. Exp. Therm. Fluid Sci. 40, 140–149.Google Scholar