Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-19T15:24:12.843Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulence in supersonic boundary layers at moderate Reynolds number

Published online by Cambridge University Press:  21 October 2011

Sergio Pirozzoli  and
Matteo Bernardini
Sergio Pirozzoli*
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Università di Roma ‘La Sapienza’, via Eudossiana 18, 00184 Roma, Italy
Matteo Bernardini
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Università di Roma ‘La Sapienza’, via Eudossiana 18, 00184 Roma, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the organization of turbulence in supersonic boundary layers through large-scale direct numerical simulations (DNS) at 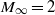, and momentum-thickness Reynolds number up to 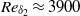(corresponding to 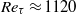) which significantly extend the current envelope of DNS in the supersonic regime. The numerical strategy relies on high-order, non-dissipative discretization of the convective terms in the Navier–Stokes equations, and it implements a recycling/rescaling strategy to stimulate the inflow turbulence. Comparison of the velocity statistics up to fourth order shows nearly exact agreement with reference incompressible data, provided the momentum-thickness Reynolds number is matched, and provided the mean velocity and the velocity fluctuations are scaled to incorporate the effects of mean density variation, as postulated by Morkovin’s hypothesis. As also found in the incompressible regime, we observe quite a different behaviour of the second-order flow statistics at sufficiently large Reynolds number, most of which show the onset of a range with logarithmic variation, typical of ‘attached’ variables, whereas the wall-normal velocity exhibits a plateau away from the wall, which is typical of ‘detached’ variables. The modifications of the structure of the flow field that underlie this change of behaviour are highlighted through visualizations of the velocity and temperature fields, which substantiate the formation of large jet-like and wake-like motions in the outer part of the boundary layer. It is found that the typical size of the attached eddies roughly scales with the local mean velocity gradient, rather than being proportional to the wall distance, as happens for the wall-detached variables. The interactions of the large eddies in the outer layer with the near-wall region are quantified through a two-point amplitude modulation covariance, which characterizes the modulating action of energetic outer-layer eddies.

JFM classification

Boundary Layers: Boundary layer structure Compressible Flows: Compressible boundary layers Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 688 , 10 December 2011 , pp. 120 - 168
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abe, H. & Antonia, R. A. 2009 Near-wall similarity between velocity and scalar fluctuations in a turbulent channel flow. Phys. Fluids 21, 025109.CrossRefGoogle Scholar
2. Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
3. del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.CrossRefGoogle Scholar
4. del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.CrossRefGoogle Scholar
5. Bernardini, M. & Pirozzoli, S. 2011a Inner/outer layer interactions in turbulent boundary layers: a refined measure for the large-scale amplitude modulation mechanism. Phys. Fluids 23, 061701.CrossRefGoogle Scholar
6. Bernardini, M. & Pirozzoli, S. 2011b Wall pressure fluctuations beneath supersonic turbulent boundary layers. Phys. Fluids 23, 085102.CrossRefGoogle Scholar
7. Bernardini, M., Pirozzoli, S. & Grasso, F. 2011 The wall pressure signature of transonic shock/boundary layer interaction. J. Fluid Mech. 671, 288–312.CrossRefGoogle Scholar
8. Bookey, P., Wyckham, C., Smits, A. J. & Martín, M. P. 2005 New experimental data of STBLI at DNS/LES accessible Reynolds numbers. AIAA Paper 2005-309.CrossRefGoogle Scholar
9. Debiève, J. F. 1983 Étude d’une interaction turbulence/onde de choc. PhD thesis, Université d’Aix-Marseille II.Google Scholar
10. van Driest, E. R. 1951 Turbulent boundary layer in compressible fluids. J. Aero. Sci. 18, 145–160.CrossRefGoogle Scholar
11. van Driest, E. R. 1956 The problem of aerodynamic heating. Aeronaut. Engng Rev. 15, 26–41.Google Scholar
12. Duan, L., Beekman, I. & Martín, M. P. 2010 Direct numerical simulation of hypersonic turbulent boundary layers. Part 2. Effect of wall temperature. J. Fluid Mech. 655, 419–445.CrossRefGoogle Scholar
13. Duan, L., Beekman, I. & Martín, M. P. 2011 Direct numerical simulation of hypersonic turbulent boundary layers. Part 3. Effect of Mach number. J. Fluid Mech. 672, 245–267.CrossRefGoogle Scholar
14. Eléna, M. & Lacharme, J. 1988 Experimental study of a supersonic turbulent boundary layer using a laser doppler anemometer. J. Méc. Théor. Appl. 7, 175–190.Google Scholar
15. Elsinga, G. E., Adrian, R. J., van Oudheusden, B. W. & Scarano, F. 2010 Three-dimensional vortex organization in a high-Reynolds-number supersonic turbulent boundary layer. J. Fluid Mech. 644, 35–50.CrossRefGoogle Scholar
16. Erm, L. P. & Joubert, J. 1991 Low Reynolds number turbulent boundary layers. J. Fluid Mech. 230, 1–44.CrossRefGoogle Scholar
17. Farabee, T. & Casarella, M. J. 1991 Spectral features of wall pressure fluctuations beneath turbulent boundary layers. Phys. Fluids 3 (10), 2410–2420.CrossRefGoogle Scholar
18. Fernholz, H. H. & Finley, P. J. 1976 A critical compilation of compressible turbulent boundary layer data. AGARDograph 223.Google Scholar
19. Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2006 Large-scale motions in a supersonic turbulent boundary layer. J. Fluid Mech. 556, 271–282.CrossRefGoogle Scholar
20. Gatski, T. B. & Bonnet, J.-P. 2009 Compressibility, Turbulence and High Speed Flow. Elsevier.Google Scholar
21. Gaviglio, J. 1987 Reynolds analogies and experimental study of heat transfer in the supersonic boundary layer. Intl J. Heat Mass Transfer 30, 911–926.CrossRefGoogle Scholar
22. George, W. K. & Castillo, L. 1997 Zero-pressure-gradient turbulent boundary layer. Appl. Mech. Rev. 50, 689–729.CrossRefGoogle Scholar
23. Guarini, S. E., Moser, R. D., Shariff, K. & Wray, A. 2000 Direct numerical simulation of a supersonic boundary layer at Mach 2.5. J. Fluid Mech. 414, 1–33.CrossRefGoogle Scholar
24. Head, M. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.CrossRefGoogle Scholar
25. Hopkins, E. J. & Inouye, M. 1971 An evaluation of theories for predicting turbulent skin friction and heat tranfer on flat plates at supersonic and hypersonic Mach numbers. AIAA J. 9, 993–1003.CrossRefGoogle Scholar
26. Hou, Y. X. 2003 Particle image velocimetry study of shock induced turbulent boundary layer separation. PhD thesis, Department of Aerospace Engineering and Engineering Mechanics, University of Texas at Austin.CrossRefGoogle Scholar
27. Hoyas, S. & Jiménez, J. 2006 Scaling of velocity fluctuations in turbulent channels up to . Phys. Fluids 18, 011702.CrossRefGoogle Scholar
28. Huang, P. G., Coleman, G. N. & Bradshaw, P. 1995 Compressible turbulent channel flows: DNS results and modelling. J. Fluid Mech. 305, 185–218.CrossRefGoogle Scholar
29. Humble, R. A., Elsinga, G. E., Scarano, F. & van Oudheusden, B. W. 2009 Three-dimensional instantaneous structure of a shock wave/turbulent boundary layer interaction. J. Fluid Mech. 622, 33–62.CrossRefGoogle Scholar
30. Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
31. Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.CrossRefGoogle Scholar
32. Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.CrossRefGoogle Scholar
33. Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 336–360.CrossRefGoogle Scholar
34. Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near–wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
35. Kennedy, C. A. & Gruber, A. 2008 Reduced aliasing formulations of the convective terms within the Navier–Stokes equations. J. Comput. Phys. 227, 1676–1700.CrossRefGoogle Scholar
36. Kim, J., Moin, P. & Moser, R. D. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
37. Komminao, J. & Skote, M. 2002 Reynolds stress budgets in Couette and boundary layer flows. Flow Turbul. Combust. 68, 167–192.CrossRefGoogle Scholar
38. Kong, H., Choi, H. & Lee, J. S. 2000 Direct numerical simulation of turbulent thermal boundary layers. Phys. Fluids 10, 85–91.Google Scholar
39. Lagha, M., Kim, J., Eldredge, J. D. & Zhong, X. 2011 A numerical study of compressible turbulent boundary layers. Phys. Fluids 23, 015106.CrossRefGoogle Scholar
40. Laufer, J. 1964 Some statistical properties of the pressure field radiated by a turbulent boundary layer. Phys. Fluids 7, 1191–1197.CrossRefGoogle Scholar
41. Maeder, T., Adams, N. A. & Kleiser, L. 2001 Direct simulation of turbulent supersonic boundary layers by an extended temporal approach. J. Fluid Mech. 429, 187–216.CrossRefGoogle Scholar
42. Martín, M. P. 2007 Direct numerical simulation of hypersonic turbulent boundary layers. Part 1. Initialization and comparison with experiments. J. Fluid Mech. 570, 347–364.CrossRefGoogle Scholar
43. Marusic, I. & Heuer, W. D. C. 2007 Reynolds number invariance of the structure inclination angle in wall turbulence. Phys. Rev. Lett. 99, 114504.CrossRefGoogle ScholarPubMed
44. Mathis, R., Hutchins, N. & Marusic, I. 2009a Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
45. Mathis, R., Monty, J. P., Hutchins, N. & Marusic, I. 2009b Comparison of large-scale amplitude modulation in turbulent boundary layers, pipes, and channel flows. Phys. Fluids 21, 111703.CrossRefGoogle Scholar
46. Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.CrossRefGoogle Scholar
47. Morkovin, M. V. 1961 Effects of compressibility on turbulent flows. In Mécanique de la Turbulence, pp. 367–380. A. Favre.Google Scholar
48. Nagib, H. M. & Chauhan, K. A. 2008 Variations of von kármán coefficient in canonical flows. Phys. Fluids 20, 101518.CrossRefGoogle Scholar
49. Perry, A. E. & Li, J. D. 1990 Experimental support for the attached-eddy hypothesis in zero-pressure-gradient turbulent boundary layers. J. Fluid Mech. 218, 405–438.CrossRefGoogle Scholar
50. Piponniau, S., Dussauge, J.-P., Debiève, J. F. & Dupont, P. 2009 A simple model for low-frequency unsteadiness in shock-induced separation. J. Fluid Mech. 629, 87–108.CrossRefGoogle Scholar
51. Pirozzoli, S. 2010 Generalized conservative approximations of split convective derivative operators. J. Comput. Phys. 229, 7180–7190.CrossRefGoogle Scholar
52. Pirozzoli, S., Bernardini, M. & Grasso, F. 2010a Direct numerical simulation of transonic shock/boundary layer interaction under conditions of incipient separation. J. Fluid Mech. 657, 361–393.CrossRefGoogle Scholar
53. Pirozzoli, S., Bernardini, M. & Grasso, F. 2010b On the dynamical relevance of coherent vortical structures in turbulent boundary layers. J. Fluid Mech. 648, 325–349.CrossRefGoogle Scholar
54. Pirozzoli, S., Grasso, F. & Gatski, T. B. 2004 Direct numerical simulation and analysis of a spatially evolving supersonic turbulent boundary layer at . Phys. Fluids 16 (3), 530–545.CrossRefGoogle Scholar
55. Poinsot, T. S. & Lele, S. K. 1992 Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 101, 104–129.CrossRefGoogle Scholar
56. Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
57. Ringuette, M. J., Wu, M. & Martín, M. P. 2008 Coherent structures in direct numerical simulation of turbulent boundary layers at Mach 3. J. Fluid Mech. 594, 59–69.CrossRefGoogle Scholar
58. Schlatter, P. & Örlü, R. 2010a Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.CrossRefGoogle Scholar
59. Schlatter, P. & Örlü, R. 2010b Quantifying the interaction between large and small scales in wall-bounded turbulent flows: a note of caution. Phys. Fluids 22, 051704.CrossRefGoogle Scholar
60. Schlatter, P., Örlü, R., Li, Q., Brethouwer, G., Fransson, J. H. M., Johansson, A. V., Alfredsson, P. H. & Henningson, D. S. 2009 Turbulent boundary layers up to studied through simulation and experiment. Phys. Fluids 21, 051702.CrossRefGoogle Scholar
61. Simens, M. P., Jiménez, J., Hoyas, S. & Mizuno, Y. 2009 A high-resolution code for a turbulent boundary layers. J. Comput. Phys. 228, 4218–4231.CrossRefGoogle Scholar
62. Smith, D. R. & Smits, A. J. 1993 The simultaneous measurement of velocity and temperature fluctuations in the boundary layer of a supersonic flow. Exp. Therm. Fluid Sci. 7, 221–229.CrossRefGoogle Scholar
63. Smith, M. W. & Smits, A. J. 1995 Visualization of he structure of supersonic turbulent boundary layers. Exp. Fluids 18, 288–302.CrossRefGoogle Scholar
64. Smits, A. J. & Dussauge, J.-P. 2006 Turbulent Shear Layers in Supersonic Flow, 2nd edn. American Institute of Physics.Google Scholar
65. Smits, A. J., Matheson, N. & Joubert, P. N. 1983 Low-Reynolds-number turbulent boundary layers in zero and favourable pressure gradients. J. Ship Res. 147–157.CrossRefGoogle Scholar
66. Smits, A. J., Spina, E. F., Alving, A. E., Smith, R. W. & Fernando, E. M. 1989 A comparison of the turbulence structure of subsonic and supersonic boundary layers. Phys. Fluids A 1, 1865–1875.CrossRefGoogle Scholar
67. Spina, E. F., Donovan, J. F. & Smits, A. J. 1991 On the structure of high-Reynolds-number supersonic turbulent boundary layers. J. Fluid Mech. 222, 293–327.CrossRefGoogle Scholar
68. Spina, E. F. & Smits, A. J. 1987 Organized structures in a compressible turbulent boundary layer. J. Fluid Mech. 182, 85–109.CrossRefGoogle Scholar
69. Spina, E. F., Smits, A. J. & Robinson, S. K. 1994 The physics of supersonic turbulent boundary layers. Annu. Rev. Fluid Mech. 26, 287–319.CrossRefGoogle Scholar
70. Stolz, S. & Adams, N. A. 2003 Large-eddy simulation of high-Reynolds-number supersonic boundary layers using the approximate deconvolution model and a rescaling and recycling technique. Phys. Fluids 15 (8), 2398–2412.CrossRefGoogle Scholar
71. Suponitsky, V., Cohen, J. & Bar-Yoseph, P. Z. 2005 The generation of streaks and hairpin vortices from a localized vortex disturbance embedded in unbounded uniform shear flow. J. Fluid Mech. 535, 65–100.CrossRefGoogle Scholar
72. Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
73. Warhaft, Z. 2000 Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 32, 203–240.CrossRefGoogle Scholar
74. Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.CrossRefGoogle Scholar
75. Xu, S. & Martin, M. P. 2004 Assessment of inflow boundary conditions for compressible turbulent boundary layers. Phys. Fluids 16 (7), 2623–2639.CrossRefGoogle Scholar