Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Taveira, Rodrigo R.
and
da Silva, Carlos B.
2013.
Kinetic energy budgets near the turbulent/nonturbulent interface in jets.
Physics of Fluids,
Vol. 25,
Issue. 1,
Watanabe, T.
Sakai, Y.
Nagata, K.
Ito, Y.
and
Hayase, T.
2014.
Enstrophy and passive scalar transport near the turbulent/non-turbulent interface in a turbulent planar jet flow.
Physics of Fluids,
Vol. 26,
Issue. 10,
da Silva, Carlos B
Taveira, Rodrigo R
and
Borrell, Guillem
2014.
Characteristics of the turbulent/nonturbulent interface in boundary layers, jets and shear-free turbulence.
Journal of Physics: Conference Series,
Vol. 506,
Issue. ,
p.
012015.
da Silva, Carlos B.
Hunt, Julian C.R.
Eames, Ian
and
Westerweel, Jerry
2014.
Interfacial Layers Between Regions of Different Turbulence Intensity.
Annual Review of Fluid Mechanics,
Vol. 46,
Issue. 1,
p.
567.
Watanabe, T.
Sakai, Y.
Nagata, K.
Ito, Y.
and
Hayase, T.
2014.
Wavelet analysis of coherent vorticity near the turbulent/non-turbulent interface in a turbulent planar jet.
Physics of Fluids,
Vol. 26,
Issue. 9,
Taveira, Rodrigo R.
and
da Silva, Carlos B.
2014.
Characteristics of the viscous superlayer in shear free turbulence and in planar turbulent jets.
Physics of Fluids,
Vol. 26,
Issue. 2,
Borrell, Guillem
and
Jiménez, Javier
2016.
Properties of the turbulent/non-turbulent interface in boundary layers.
Journal of Fluid Mechanics,
Vol. 801,
Issue. ,
p.
554.
Watanabe, T.
Jaulino, R.
Taveira, R. R.
da Silva, C. B.
Nagata, K.
and
Sakai, Y.
2017.
Role of an isolated eddy near the turbulent/non-turbulent interface layer.
Physical Review Fluids,
Vol. 2,
Issue. 9,
Watanabe, Tomoaki
da Silva, Carlos B.
Nagata, Koji
and
Sakai, Yasuhiko
2017.
Geometrical aspects of turbulent/non-turbulent interfaces with and without mean shear.
Physics of Fluids,
Vol. 29,
Issue. 8,
Johnson, Blair A.
and
Cowen, Edwin A.
2018.
Turbulent boundary layers absent mean shear.
Journal of Fluid Mechanics,
Vol. 835,
Issue. ,
p.
217.
Silva, Tiago S.
Zecchetto, Marco
and
da Silva, Carlos B.
2018.
The scaling of the turbulent/non-turbulent interface at high Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 843,
Issue. ,
p.
156.
Elsinga, G. E.
and
da Silva, C. B.
2019.
How the turbulent/non-turbulent interface is different from internal turbulence.
Journal of Fluid Mechanics,
Vol. 866,
Issue. ,
p.
216.
Watanabe, Tomoaki
da Silva, Carlos B.
and
Nagata, Koji
2019.
Non-dimensional energy dissipation rate near the turbulent/non-turbulent interfacial layer in free shear flows and shear free turbulence.
Journal of Fluid Mechanics,
Vol. 875,
Issue. ,
p.
321.
Nagata, Ryosuke
Watanabe, Tomoaki
Nagata, Koji
and
da Silva, Carlos B.
2020.
Triple decomposition of velocity gradient tensor in homogeneous isotropic turbulence.
Computers & Fluids,
Vol. 198,
Issue. ,
p.
104389.
Tanaka, K.
Watanabe, T.
and
Nagata, K.
2020.
Statistical analysis of deformation of a shock wave propagating in a local turbulent region.
Physics of Fluids,
Vol. 32,
Issue. 9,
Xavier, Ricardo P.
Teixeira, Miguel A. C.
and
da Silva, Carlos B.
2021.
Asymptotic scaling laws for the irrotational motions bordering a turbulent region.
Journal of Fluid Mechanics,
Vol. 918,
Issue. ,
Zecchetto, Marco
and
da Silva, Carlos B.
2021.
Universality of small-scale motions within the turbulent/non-turbulent interface layer.
Journal of Fluid Mechanics,
Vol. 916,
Issue. ,
Kalluri, Manohar Teja
and
Narasimhamurthy, Vagesh D.
2022.
Shear-layer dynamics at the interface of parallel Couette flows.
Physics of Fluids,
Vol. 34,
Issue. 10,
Abreu, Hugo
Pinho, Fernando T.
and
da Silva, Carlos B.
2022.
Turbulent entrainment in viscoelastic fluids.
Journal of Fluid Mechanics,
Vol. 934,
Issue. ,
Zecchetto, Marco
Xavier, Ricardo P.
Teixeira, Miguel A. C.
and
da Silva, Carlos B.
2024.
Generalized scaling laws for the irrotational motions bordering a turbulent region.
Physical Review E,
Vol. 109,
Issue. 6,
 ), turbulence length scales, and pressure statistics are derived, showing an excellent agreement with results from direct numerical simulations (DNS). Interestingly, the normalized inviscid flow statistics at the T/NT interface do not depend on the form of the assumed TKE spectrum. Outside the turbulent region, where the flow is irrotational (except inside a thin viscous boundary layer),
), turbulence length scales, and pressure statistics are derived, showing an excellent agreement with results from direct numerical simulations (DNS). Interestingly, the normalized inviscid flow statistics at the T/NT interface do not depend on the form of the assumed TKE spectrum. Outside the turbulent region, where the flow is irrotational (except inside a thin viscous boundary layer),  decays as
decays as 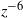 , where
, where  is the distance from the T/NT interface. The mean pressure distribution is calculated using RDT, and exhibits a decrease towards the turbulence region due to the associated velocity fluctuations, consistent with the generation of a mean entrainment velocity. The vorticity variance and
is the distance from the T/NT interface. The mean pressure distribution is calculated using RDT, and exhibits a decrease towards the turbulence region due to the associated velocity fluctuations, consistent with the generation of a mean entrainment velocity. The vorticity variance and  display large maxima at the T/NT interface due to the inviscid discontinuities of the tangential velocity variances existing there, and these maxima are quantitatively related to the thickness
display large maxima at the T/NT interface due to the inviscid discontinuities of the tangential velocity variances existing there, and these maxima are quantitatively related to the thickness 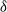 of the viscous boundary layer (VBL). For an equilibrium VBL, the RDT analysis suggests that
of the viscous boundary layer (VBL). For an equilibrium VBL, the RDT analysis suggests that 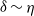 (where
(where 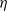 is the Kolmogorov microscale), which is consistent with the scaling law identified in a very recent DNS study for shear-free T/NT interfaces.
is the Kolmogorov microscale), which is consistent with the scaling law identified in a very recent DNS study for shear-free T/NT interfaces.