Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Steiros, K.
Bruce, P. J. K.
Buxton, O. R. H.
and
Vassilicos, J. C.
2017.
Effect of blade modifications on the torque and flow field of radial impellers in stirred tanks.
Physical Review Fluids,
Vol. 2,
Issue. 9,
Alves Portela, F.
Papadakis, G.
and
Vassilicos, J. C.
2018.
Turbulence dissipation and the role of coherent structures in the near wake of a square prism.
Physical Review Fluids,
Vol. 3,
Issue. 12,
Miyanawala, T.P.
and
Jaiman, R.K.
2018.
Self-sustaining turbulent wake characteristics in fluid–structure interaction of a square cylinder.
Journal of Fluids and Structures,
Vol. 77,
Issue. ,
p.
80.
Yasuda, T.
and
Vassilicos, J. C.
2018.
Spatio-temporal intermittency of the turbulent energy cascade.
Journal of Fluid Mechanics,
Vol. 853,
Issue. ,
p.
235.
Lai, Chris C. K.
Charonko, John J.
and
Prestridge, Katherine
2018.
A Kármán–Howarth–Monin equation for variable-density turbulence.
Journal of Fluid Mechanics,
Vol. 843,
Issue. ,
p.
382.
Carter, Douglas W.
and
Coletti, Filippo
2018.
Small-scale structure and energy transfer in homogeneous turbulence.
Journal of Fluid Mechanics,
Vol. 854,
Issue. ,
p.
505.
Zhou, Yi
Nagata, Koji
Sakai, Yasuhiko
and
Watanabe, Tomoaki
2018.
Dual-plane turbulent jets and their non-Gaussian velocity fluctuations.
Physical Review Fluids,
Vol. 3,
Issue. 12,
Lander, D. C.
Moore, D. M.
Letchford, C. W.
and
Amitay, M.
2018.
Scaling of square-prism shear layers.
Journal of Fluid Mechanics,
Vol. 849,
Issue. ,
p.
1096.
Bagkeris, Ioannis
Michael, Vipin
Prosser, Robert
and
Kowalski, Adam
2019.
WITHDRAWN: Large-eddy simulation in a Sonolator high-pressure homogeniser.
Chemical Engineering Science: X,
p.
100052.
Bagkeris, Ioannis
Michael, Vipin
Prosser, Robert
and
Kowalski, Adam J.
2019.
Simulation of Turbulent Emulsification in a Sonolator Mixer: Interpretation of Drop Breakage Time.
Chemical Engineering & Technology,
Vol. 42,
Issue. 8,
p.
1555.
Gatti, Davide
Remigi, Alberto
Chiarini, Alessandro
Cimarelli, Andrea
and
Quadrio, Maurizio
2019.
An efficient numerical method for the generalised Kolmogorov equation.
Journal of Turbulence,
Vol. 20,
Issue. 8,
p.
457.
Zhou, Yi
Nagata, Koji
Sakai, Yasuhiko
and
Watanabe, Tomoaki
2019.
Extreme events and non-Kolmogorov spectra in turbulent flows behind two side-by-side square cylinders.
Journal of Fluid Mechanics,
Vol. 874,
Issue. ,
p.
677.
Luan, Xin
Mao, Beibei
Ren, Xinmin
Yang, Hua
Teng, Yuru
and
Song, Dalei
2019.
Turbulent Cascade in the Multi-layered Network.
p.
1.
Tsinober, Arkady
2019.
The Essence of Turbulence as a Physical Phenomenon.
p.
47.
Tao, Shancong
and
Zhou, Yi
2019.
Turbulent flows around side-by-side cylinders with regular and multiscale arrangements.
Physical Review Fluids,
Vol. 4,
Issue. 12,
Bagkeris, Ioannis
Michael, Vipin
Prosser, Robert
and
Kowalski, Adam
2020.
Large–eddy simulation in a Sonolator high–pressure homogeniser.
Chemical Engineering Science,
Vol. 215,
Issue. ,
p.
115441.
Knutsen, Anna N.
Baj, Pawel
Lawson, John M.
Bodenschatz, Eberhard
Dawson, James R.
and
Worth, Nicholas A.
2020.
The inter-scale energy budget in a von Kármán mixing flow.
Journal of Fluid Mechanics,
Vol. 895,
Issue. ,
Yao, H.
Alves-Portela, F.
and
Papadakis, G.
2020.
Evolution of conditionally averaged second-order structure functions in a transitional boundary layer.
Physical Review Fluids,
Vol. 5,
Issue. 9,
Alves Portela, F.
Papadakis, G.
and
Vassilicos, J. C.
2020.
The role of coherent structures and inhomogeneity in near-field interscale turbulent energy transfers.
Journal of Fluid Mechanics,
Vol. 896,
Issue. ,
Yasuda, Tatsuya
Goto, Susumu
and
Vassilicos, John Christos
2020.
Formation of power-law scalings of spectra and multiscale coherent structures in the near-field of grid-generated turbulence.
Physical Review Fluids,
Vol. 5,
Issue. 1,
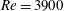 $Re=3900$ using the Kármán–Howarth–Monin–Hill equation. This is the fully generalised scale-by-scale energy balance which, unlike the Kármán–Howarth equation, does not require homogeneity or isotropy assumptions. Our data are obtained from a direct numerical simulation and therefore enable us to access all of the processes involved in this energy balance. A significant range of length scales exists where the orientation-averaged nonlinear interscale transfer rate is approximately constant and negative, indicating a forward turbulence cascade on average. This average cascade consists of coexisting forward and inverse cascade behaviours in different scale-space orientations. With increasing distance from the prism but within the near field of the wake, the orientation-averaged nonlinear interscale transfer rate tends to be approximately equal to minus the turbulence dissipation rate even though all of the inhomogeneity-related energy processes in the scale-by-scale energy balance are significant, if not equally important. We also find well-defined near
$Re=3900$ using the Kármán–Howarth–Monin–Hill equation. This is the fully generalised scale-by-scale energy balance which, unlike the Kármán–Howarth equation, does not require homogeneity or isotropy assumptions. Our data are obtained from a direct numerical simulation and therefore enable us to access all of the processes involved in this energy balance. A significant range of length scales exists where the orientation-averaged nonlinear interscale transfer rate is approximately constant and negative, indicating a forward turbulence cascade on average. This average cascade consists of coexisting forward and inverse cascade behaviours in different scale-space orientations. With increasing distance from the prism but within the near field of the wake, the orientation-averaged nonlinear interscale transfer rate tends to be approximately equal to minus the turbulence dissipation rate even though all of the inhomogeneity-related energy processes in the scale-by-scale energy balance are significant, if not equally important. We also find well-defined near 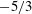 $-5/3$ energy spectra in the streamwise direction, in particular at a centreline position where the inverse cascade behaviour occurs for streamwise oriented length scales.
$-5/3$ energy spectra in the streamwise direction, in particular at a centreline position where the inverse cascade behaviour occurs for streamwise oriented length scales.


