Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-01T00:28:44.410Z Has data issue: false hasContentIssue false
  • English
  • Français

Transitional flows with the entropic lattice Boltzmann method

Published online by Cambridge University Press:  05 July 2017

B. Dorschner ,
S. S. Chikatamarla  and
I. V. Karlin Open the ORCID record for I. V. Karlin [Opens in a new window]
B. Dorschner
Affiliation:
Aerothermochemistry and Combustion Systems Laboratory, Institute of Energy Technology, Department of Mechanical and Process Engineering, ETH Zurich, 8092 Zurich, Switzerland
S. S. Chikatamarla
Affiliation:
Aerothermochemistry and Combustion Systems Laboratory, Institute of Energy Technology, Department of Mechanical and Process Engineering, ETH Zurich, 8092 Zurich, Switzerland
I. V. Karlin*
Affiliation:
Aerothermochemistry and Combustion Systems Laboratory, Institute of Energy Technology, Department of Mechanical and Process Engineering, ETH Zurich, 8092 Zurich, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

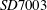The accuracy and performance of entropic multi-relaxation time lattice Boltzmann models are assessed for transitional flows of engineering interest. A simulation of the flow over a low-Reynolds-number $SD7003$ airfoil at 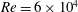$Re=6\times 10^{4}$, at an angle of attack 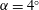$\unicode[STIX]{x1D6FC}=4^{\circ }$, is performed and thoroughly compared to available numerical and experimental data. In order to include blockage and curvature effects, simulations of the flow in a low-pressure turbine passage composed of 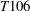$T106$ blade profiles, at a chord Reynolds number of 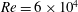$Re=6\times 10^{4}$ or 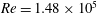$Re=1.48\times 10^{5}$, for different free-stream turbulence intensities are presented. Using a multi-domain grid refinement strategy in combination with Grad’s boundary conditions yields good agreement for all simulations. The results demonstrate that the entropic lattice Boltzmann model is a viable, parameter-free alternative to modelling approaches such as large-eddy simulations with similar resolution requirements.

JFM classification

Boundary Layers: Boundary layer separation Boundary Layers: Boundary layer stability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 824 , 10 August 2017 , pp. 388 - 412
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahuja, K. & Burrin, R. 1984 Control of flow separation by sound. In 9th Aeroacoustics Conference, p. 2298. American Institute for Aeronautics and Astronautics.Google Scholar
Alam, M. & Sandham, N. D. 2000 Direct numerical simulation of ‘short’ laminar separation bubbles with turbulent reattachment. J. Fluid Mech. 410, 1–28.Google Scholar
Balzer, W. & Fasel, H. 2010 Direct numerical simulation of laminar boundary-layer separation and separation control on the suction side of an airfoil at low Reynolds number conditions. In 40th Fluid Dynamics Conference and Exhibit, p. 4866. American Institute for Aeronautics and Astronautics.Google Scholar
Bigoni, F., Vagnoli, S., Arts, T. & Verstraete, T. 2016 Detailed numerical characterization of the suction side laminar separation bubble for a high-lift low pressure turbine blade by means of RANS and LES. In ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, pp. V02DT44A015–V02DT44A015. American Society of Mechanical Engineers.Google Scholar
Boiko, A. V., Grek, G. R., Dovgal, A. V. & Kozlov, V. V. 2002 The Origin of Turbulence in Near-wall Flows. Springer.Google Scholar
Bösch, F., Chikatamarla, S. S. & Karlin, I. 2015a Entropic multi-relaxation models for simulation of fluid turbulence. ESAIM: Proc. Surveys 52, 1–24.Google Scholar
Bösch, F., Chikatamarla, S. S. & Karlin, I. V. 2015b Entropic multirelaxation lattice Boltzmann models for turbulent flows. Phys. Rev. E 92 (4), 43309.Google ScholarPubMed
Boutilier, M. S. H. & Yarusevych, S. 2012a Separated shear layer transition over an airfoil at a low Reynolds number. Phys. Fluids 24 (8), 084105.Google Scholar
Boutilier, M. S. H. & Yarusevych, S. 2012b Parametric study of separation and transition characteristics over an airfoil at low Reynolds numbers. Exp. Fluids 52 (6), 1491–1506.Google Scholar
Burgmann, S., Dannemann, J. & Schröder, W. 2008 Time-resolved and volumetric PIV measurements of a transitional separation bubble on an SD7003 airfoil. Exp. Fluids 44 (4), 609–622.Google Scholar
Cadieux, F. & Domaradzki, J. A. 2015 Performance of subgrid-scale models in coarse large eddy simulations of a laminar separation bubble. Phys. Fluids 27 (4), 045112.Google Scholar
Cadieux, F., Domaradzki, J. A., Sayadi, T. & Bose, S. 2014 Direct numerical simulation and large eddy simulation of laminar separation bubbles at moderate Reynolds numbers. Trans. ASME J. Fluids Engng 136 (6), 60902.Google Scholar
Chen, H., Kandasamy, S., Orszag, S., Shock, R., Succi, S. & Yakhot, V. 2003 Extended Boltzmann kinetic equation for turbulent flows. Science 301 (5633), 633–636.CrossRefGoogle ScholarPubMed
Dorschner, B., Bösch, F., Chikatamarla, S. S., Boulouchos, K. & Karlin, I. V. 2016a Entropic multi-relaxation time lattice Boltzmann model for complex flows. J. Fluid Mech. 801, 623–651.Google Scholar
Dorschner, B., Chikatamarla, S. S., Bösch, F. & Karlin, I. V. 2015 Grad’s approximation for moving and stationary walls in entropic lattice Boltzmann simulations. J. Comput. Phys. 295, 340–354.Google Scholar
Dorschner, B., Chikatamarla, S. S. & Karlin, I. V.2016b Entropic lattice Boltzmann method for moving and deforming geometries in three dimensions. Phys. Rev. E (in press), arXiv:1608.04658.Google Scholar
Dorschner, B., Frapolli, N., Chikatamarla, S. S. & Karlin, I. V. 2016c Grid refinement for entropic lattice Boltzmann models. Phys. Rev. E 94, 053311.Google ScholarPubMed
Dovgal, A. V., Kozlov, V. V. & Michalke, A. 1994 Laminar boundary layer separation: instability and associated phenomena. Prog. Aerosp. Sci. 30 (1), 61–94.CrossRefGoogle Scholar
Eisenbach, S. & Friedrich, R. 2008 Large-eddy simulation of flow separation on an airfoil at a high angle of attack and Re = 105 using Cartesian grids. Theor. Comput. Fluid Dyn. 22 (3–4), 213–225.Google Scholar
Engber, M. & Fottner, L. 1996 The effect of incoming wakes on boundary layer transition of a highly loaded turbine cascade. AGARD CP 571, 21.Google Scholar
Fung, J. C. H., Hunt, J. C., Malik, N. A. & Perkins, R. J. 1992 Kinematic simulation of homogeneous turbulence by unsteady random Fourier modes. J. Fluid Mech. 236, 281–318.Google Scholar
Galbraith, M. C. & Visbal, M. R. 2008 Implicit large eddy simulation of low Reynolds number flow past the SD7003 airfoil. AIAA Paper 225, 1–17.Google Scholar
Gaster, M.1963 On the stability of parallel flows and the behaviour of separation bubbles. PhD thesis, Queen Mary, University of London.Google Scholar
Gaster, M. 1992 Stability of velocity profiles with reverse flow. In Instability, Transition, and Turbulence, pp. 212–215. Springer.Google Scholar
Gaster, M. 2006 Laminar separation bubbles. In Sixth IUTAM Symposium on Laminar-Turbulent Transition, pp. 1–13. Springer.Google Scholar
Gerakopulos, R., Boutilier, M. & Yarusevych, S. 2010 Aerodynamic characterization of a NACA 0018 airfoil at low Reynolds numbers. In 40th Fluid dynamics conference and Exhibit, p. 4629. American Institute of Aeronautics and Astronautics.Google Scholar
Hadzic, I. & Hanjalic, K. 2000 Separation-induced transition to turbulence: second-moment closure modelling. Flow Turbul. Combust. 63, 153–173.Google Scholar
Hain, R., Kähler, C. J. & Radespiel, R. 2009 Dynamics of laminar separation bubbles at low-Reynolds-number aerofoils. J. Fluid Mech. 630, 129–153.Google Scholar
Higuera, F. J. & Jimenez, J. 1989 Boltzmann approach to lattice gas simulations. Europhys. Lett. 9 (7), 663.Google Scholar
Higuera, F. J. & Succi, S. 1989 Simulating the flow around a circular cylinder with a lattice Boltzmann equation. Europhys. Lett. 8 (6), 517.Google Scholar
Higuera, F. J., Succi, S. & Benzi, R. 1989 Lattice gas dynamics with enhanced collisions. Europhys. Lett. 9 (4), 345.Google Scholar
Hilgenfeld, L., Stadtmüller, P. & Fottner, L. 2002 Experimental investigation of turbulence influence of wake passing on the boundary layer development of highly loaded turbine cascade blades. Flow Turbul. Combust. 69 (3–4), 229–247.Google Scholar
Ho, C.-M. & Huerre, P. 1984 Perturbed free shear layers. Annu. Rev. Fluid Mech. 16 (1), 365–422.Google Scholar
Hodson, H. 2000 Turbulence modelling for unsteady flows in axial turbine: turmunsflat. In Brite-Euram Project, Final Tech. Rep. CT96-1043, von Karman Institute, pp. 85–99.Google Scholar
Howard, R. J. A., Alam, M. & Sandham, N. D. 2000 Two-equation turbulence modelling of a transitional separation bubble. Flow Turbul. Combust. 63 (1), 175–191.Google Scholar
d’Humieres, D. 1992 Rarefied gas dynamics: theory and simulations. Prog. Aeronaut. Astronaut. 159, 450–458.Google Scholar
Jones, L. E. & Sandberg, R. D. 2011 Numerical analysis of tonal airfoil self-noise and acoustic feedback-loops. J. Sound Vib. 330 (25), 6137–6152.Google Scholar
Jones, L. E., Sandberg, R. D. & Sandham, N. D. 2008 Direct numerical simulations of forced and unforced separation bubbles on an airfoil at incidence. J. Fluid Mech. 602, 175–207.Google Scholar
Jones, L. E., Sandberg, R. D. & Sandham, N. D. 2010 Stability and receptivity characteristics of a laminar separation bubble on an aerofoil. J. Fluid Mech. 48 (2), 414–426.Google Scholar
Karlin, I. V., Bösch, F. & Chikatamarla, S. S. 2014 Gibbs’ principle for the lattice-kinetic theory of fluid dynamics. Phys. Rev. E 90 (3), 31302.Google Scholar
Karlin, I. V., Ferrante, A. & Öttinger, H. C. 1999 Perfect entropy functions of the lattice Boltzmann method. Europhys. Lett. 47 (2), 182–188.Google Scholar
Kurelek, J. W., Lambert, A. R. & Yarusevych, S. 2016 Coherent structures in the transition process of a laminar separation bubble. AIAA J. 54 (8), 1–15.Google Scholar
Lang, M., Rist, U. & Wagner, S. 2004 Investigations on controlled transition development in a laminar separation bubble by means of LDA and PIV. Exp. Fluids 36 (1), 43–52.Google Scholar
Latt, J. & Chopard, B. 2006 Lattice Boltzmann method with regularized pre-collision distribution functions. Maths Comput. Simul. 72 (2–6), 165–168.Google Scholar
Malaspinas, O. & Sagaut, P. 2012 Consistent subgrid scale modelling for lattice Boltzmann methods. J. Fluid Mech. 700, 514–542.CrossRefGoogle Scholar
Marxen, O., Lang, M., Rist, U. & Wagner, S. 2003 A combined experimental/numerical study of unsteady phenomena in a laminar separation bubble. Flow Turbul. Combust. 71 (1), 133–146.Google Scholar
Marxen, O. & Rist, U. 2010 Mean flow deformation in a laminar separation bubble: separation and stability characteristics. J. Fluid Mech. 660, 37–54.Google Scholar
Marxen, O., Rist, U. & Wagner, S. 2004 Effect of spanwise-modulated disturbances on transition in a separated boundary layer. AIAA J. 42 (5), 937–944.Google Scholar
Maucher, U.2002 Numerical investigations on the transition in the laminar separation bubble in an airfoil boundary layer. PhD thesis, University of Stuttgart.Google Scholar
Maucher, U., Rist, U. & Wagner, S. 1997 Secondary instabilities in a laminar separation bubble. In New results in Numerical and Experimental Fluid Mechanics, pp. 229–236. Vieweg+Teubner.Google Scholar
Maucher, U., Rist, U. & Wagner, S. 1999 Transitional structures in a laminar separation bubble. In New Results in Numerical and Experimental Fluid Mechanics II, pp. 307–314. Springer.Google Scholar
Mayle, R. E. 1991 The 1991 IGTI scholar lecture: the role of laminar-turbulent transition in gas turbine engines. Trans. ASME J. Turbomach. 113 (4), 509–536.Google Scholar
McAuliffe, B. R. & Yaras, M. I. 2005 Separation-bubble-transition measurements on a low-Re airfoil using particle image velocimetry. In ASME Turbo Expo 2005: Power for Land, Sea, and Air, pp. 1029–1038. American Society of Mechanical Engineers.Google Scholar
Michelassi, V., Wissink, J. G. & Rodi, W. 2003 Large-eddy simulation of flow around low-pressure turbine blade with incoming wakes. AIAA J. 41 (11), 2143–2156.Google Scholar
Michelassi, V., Wissink, J. & Rodi, W. 2002 Analysis of DNS and LES of flow in a low pressure turbine cascade with incoming wakes and comparison with experiments. Flow Turbul. Combust. 69 (3–4), 295–330.Google Scholar
Mittal, R., Venkatasubramanian, S. & Najjar, F. M. 2001 Large-eddy simulation of flow through a low-pressure turbine cascade. Mech. Engng 1–9.Google Scholar
Ol, M., McCauliffe, B., Hanff, E., Scholz, U. & Kaehler, C. 2005 Comparison of laminar separation bubble measurements on a low Reynolds number airfoil in three facilities. In 35th AIAA Fluid Dynamics Conference and Exhibit, p. 5149. American Institute for Aeronautics and Astronautics.Google Scholar
O’meara, M. & Mueller, T. 1987 Laminar separation bubble characteristics on an airfoil at low Reynolds numbers. AIAA J. 25 (8), 1033–1041.Google Scholar
Papanicolaou, E. L. & Rodi, W. 1999 Computation of separated-flow transition using a two-layer model of turbulence. Trans. ASME J. Turbomach. 121 (January 1999), 78–87.Google Scholar
Raverdy, B., Mary, I., Sagaut, P. & Liamis, N. 2003 High-resolution large-eddy simulation of flow around low-pressure turbine blade. AIAA J. 41 (3), 390–397.Google Scholar
Rist, U. & Maucher, U. 2002 Investigations of time-growing instabilities in laminar separation bubbles. Eur. J. Mech. (B/Fluids) 21 (5), 495–509.Google Scholar
Rist, U., Maucher, U. & Wagner, S. 1996 Direct numerical simulation of some fundamental problems related to transition in laminar separation bubbles. In Proceedings of the ECCOMAS Computational Fluid Dynamics Conference, pp. 319–325. Wiley.Google Scholar
Roberts, S. K. & Yaras, M. I. 2006 Large-eddy simulation of transition in a separation bubble. Trans. ASME J. Fluids Engng 128 (2), 232.Google Scholar
Rodi, W. 2006 DNS and LES of some engineering flows. Fluid Dyn. Res. 38 (2–3), 145–173.Google Scholar
Schlichting, H., Gersten, K., Krause, E., Oertel, H. & Mayes, K. 1960 Boundary-Layer Theory. vol. 7. Springer.Google Scholar
Schulte, V. & Hodson, H. 1994 Wake-separation bubble interaction in low pressure turbines. In 30th Joint Propulsion Conference and Exhibit, American Institute of Aeronautics and Astronautics.Google Scholar
Schulte, V. & Hodson, H. P. 1998 Unsteady wake-induced boundary layer transition in high lift LP turbines. Trans. ASME J. Turbomach. 120 (1), 28.Google Scholar
Sieverding, C.2000 Simulation of a wake-blade interaction. Tech. Rep., Brite EURAM Project TURMUNSFLAT, CT96-0143, 2000, Final Report.Google Scholar
Spalart, P. R. & Strelets, M. K. 2000 Mechanisms of transition and heat transfer in a separation bubble. J. Fluid Mech. 403, 329–349.Google Scholar
Stieger, R. D. & Hodson, H. P. 2003 The transition mechanism of highly-loaded LP turbine blades. ASME Conf. Proc. 2003 (36886), 779–788.Google Scholar
Succi, S. 2015 Lattice Boltzmann 2038. Europhys. Lett. 109 (5), 50001.Google Scholar
Tani, I. 1964 Low-speed flows involving bubble separations. Prog. Aerosp. Sci. 5, 70–103.Google Scholar
Visbal, M. R. 2009 High-fidelity simulation of transitional flows past a plunging airfoil. AIAA J. 47 (January), 2685–2697.CrossRefGoogle Scholar
Watmuff, J. H. 1999 Evolution of a wave packet into vortex loops in a laminar separation bubble. J. Fluid Mech. 397, 119–169.Google Scholar
Wilson, P. G. & Pauley, L. L. 1998 Two- and three-dimensional large-eddy simulations of a transitional separation bubble. Phys. Fluids 10 (11), 2932.Google Scholar
Wissink, J. & Rodi, W. 2004 DNS of a laminar separation bubble affected by free-stream disturbances. In Direct and Large-Eddy Simulation V, pp. 213–220. Springer.Google Scholar
Wu, X. & Durbin, P. A. 2001 Evidence of longitudinal vortices evolved from distorted wakes in a turbine passage. J. Fluid Mech. 446, 199–228.Google Scholar
Wu, X., Jacobs, R. G., Hunt, J. C. & Durbin, P. A. 1999 Simulation of boundary layer transition induced by periodically passing wakes. J. Fluid Mech. 398, 109–153.Google Scholar
Xu, T., Sullivan, P. & Paraschivoiu, M. 2010 Fast large-eddy simulation of low Reynolds number flows over a NACA0025. J. Aircraft 47 (1), 328–333.Google Scholar
Yang, Z. & Voke, P. R. 2001 Large-eddy simulation of boundary-layer separation and transition at a change of surface curvature. J. Fluid Mech. 439, 305–333.Google Scholar
Yarusevych, S., Kawall, J. G. & Sullivan, P. E. 2008 Separated-shear-layer development on an airfoil at low Reynolds numbers. AIAA J. 46 (12), 3060–3069.Google Scholar
Yarusevych, S., Sullivan, P. E. & Kawall, J. G. 2006 Coherent structures in an airfoil boundary layer and wake at low Reynolds numbers. Phys. Fluids 18 (4).Google Scholar
Yarusevych, S., Sullivan, P. E. & Kawall, J. G. 2009 On vortex shedding from an airfoil in low-Reynolds-number flows. J. Fluid Mech. 632, 245–271.CrossRefGoogle Scholar
Yuan, W., Khalid, M., Windte, J., Scholz, U. & Radespiel, R. 2005 An investigation of low-Reynolds-number flows past airfoils. In 23rd AIAA Applied Aerodynamics Conference (July 2015), pp. 1–19. American Institute for Aeronautics and Astronautics.Google Scholar
Zhang, W., Hain, R. & Kähler, C. J. 2008 Scanning PIV investigation of the laminar separation bubble on a SD7003 airfoil. Exp. Fluids 45 (4), 725–743.CrossRefGoogle Scholar
Zhang, W., Zou, Z., Qi, L., Ye, J. & Wang, L. 2015 Effects of freestream turbulence on separated boundary layer in a low-Re high-lift LP turbine blade. Comput. Fluids 109, 1–12.CrossRefGoogle Scholar
Zhou, Y. & Wang, Z. J. 2010 Implicit large eddy simulation of transitional flow over a SD7003 wing using high-order spectral difference method. In 40th Fluid Dynamics Conference and Exhibit, p. 2010. American Institute for Aeronautics and Astronautics.Google Scholar