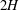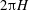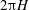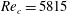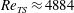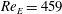1 Introduction
The application of ideas from dynamical systems theory to the turbulence transition in flows without linear instability of the laminar profile, such as pipe flow or plane Couette flow, have provided a framework in which many of the observed phenomena can be rationalized. This includes the sensitive dependence on initial conditions (Darbyshire & Mullin Reference Darbyshire and Mullin1995; Schmiegel & Eckhardt Reference Schmiegel and Eckhardt1997), the appearance of exact coherent states around which the turbulent state can form (Nagata Reference Nagata1990; Clever & Busse Reference Clever and Busse1997; Waleffe Reference Waleffe1998; Faisst & Eckhardt Reference Faisst and Eckhardt2003; Wedin & Kerswell Reference Wedin and Kerswell2004; Gibson, Halcrow & Cvitanović Reference Gibson, Halcrow and Cvitanović2009), the transience of the turbulent state (Brosa Reference Brosa1989; Bottin et al. Reference Bottin, Daviaud, Manneville and Dauchot1998; Hof et al. Reference Hof, Westerweel, Schneider and Eckhardt2006; Schneider & Eckhardt Reference Schneider and Eckhardt2008; Kreilos & Eckhardt Reference Kreilos and Eckhardt2012), or the complex spatio-temporal dynamics in large systems (Bottin et al. Reference Bottin, Daviaud, Manneville and Dauchot1998; Barkley & Tuckerman Reference Barkley and Tuckerman2005; Manneville Reference Manneville2009; Moxey & Barkley Reference Moxey and Barkley2010; Avila et al. Reference Avila, Moxey, de Lozar, Avila, Barkley and Hof2011). Extensions to open external flows, such as asymptotic suction boundary layers (Kreilos et al. Reference Kreilos, Veble, Schneider and Eckhardt2013; Khapko et al. Reference Khapko, Kreilos, Schlatter, Duguet, Eckhardt and Henningson2013, Reference Khapko, Duguet, Kreilos, Schlatter, Eckhardt and Henningson2014, Reference Khapko, Kreilos, Schlatter, Duguet, Eckhardt and Henningson2016) and developing boundary layers (Cherubini et al. Reference Cherubini, De Palma, Robinet and Bottaro2011a ; Duguet et al. Reference Duguet, Schlatter, Henningson and Eckhardt2012; Wedin et al. Reference Wedin, Bottaro, Hanifi and Zampogna2014), have been proposed.
Plane Poiseuille flow (PPF), the pressure-driven flow between parallel plates, shows a transition to turbulence near a Reynolds number of approximately 1000 (Carlson, Widnall & Peeters Reference Carlson, Widnall and Peeters1982; Lemoult, Aider & Wesfreid Reference Lemoult, Aider and Wesfreid2012; Tuckerman et al. Reference Tuckerman, Kreilos, Schrobsdorff, Schneider and Gibson2014). In the subcritical range the flow shows much of the transition phenomenology observed in other subcritical flows, such as plane Couette flow or pipe flow, but it also has a linear instability of the laminar profile at a Reynolds number of 5772 (Orszag Reference Orszag1971). This raises a question about the relation between the transition via an instability to the formation of Tollmien–Schlichting (TS) waves and the transition triggered by large-amplitude perturbations that do not need the linear instability (henceforth referred to as the ‘bypass’ transition) (Schmid & Henningson Reference Schmid and Henningson2001). For instance, one could imagine that the exact coherent structures related to the bypass transition are connected to the TS waves in some kind of subcritical bifurcation. That, however, would require a connection between the two very different flow structures: the exact coherent structures that are dominated by downstream vortices (Zammert & Eckhardt Reference Zammert and Eckhardt2014, Reference Zammert and Eckhardt2015), and the TS waves that are dominated by spanwise vortices.
Many studies of the transition to turbulence have focused on the identification of optimal perturbations that are distinguished by being the smallest ones that can trigger the transition (Farrell Reference Farrell1988; Butler & Farrell Reference Butler and Farrell1992; Duguet, Brandt & Larsson Reference Duguet, Brandt and Larsson2010; Cherubini et al. Reference Cherubini, De Palma, Robinet and Bottaro2011b ; Monokrousos et al. Reference Monokrousos, Bottaro, Brandt, Di Vita and Henningson2011; Pringle, Willis & Kerswell Reference Pringle, Willis and Kerswell2012; Duguet et al. Reference Duguet, Monokrousos, Brandt and Henningson2013). With a suitable choice of norm (for example, energy density or dissipation) this leads to an optimization problem that can be solved with suitable adjoint techniques (see Schmid (Reference Schmid2007) and Kerswell, Pringle & Willis (Reference Kerswell, Pringle and Willis2014) for reviews of the method and the connection to the dynamics in the state space of the system). In the presence of two possible routes to turbulence, via the Tollmien–Schlichting states and the bypass transition, one can expect that there are two different kinds of optimal perturbation, one for each route, but they have not been determined.
As an alternative to the determination of the optimal perturbations, we here use direct numerical simulations to map out the regions of initial conditions that follow one or the other path. Given the high dimensionality of the space, we can explore a subset of initial conditions only, and choose a plane that contains both transition states. Such explorations of the state space of a flow have been useful in the identification of the sensitive dependence on initial conditions for the transition (Schmiegel & Eckhardt Reference Schmiegel and Eckhardt1997; Faisst & Eckhardt Reference Faisst and Eckhardt2004), and in the exploration of the bifurcations (Kreilos & Eckhardt Reference Kreilos and Eckhardt2012; Kreilos, Eckhardt & Schneider Reference Kreilos, Eckhardt and Schneider2014).
We start with a description of the system and the bifurcations of the relevant coherent states in § 2. Afterwards, in § 3, we describe the exploration of the state space of the system, and continue with an description of the influence of the operating conditions in § 4. Conclusions are summarized in § 5.
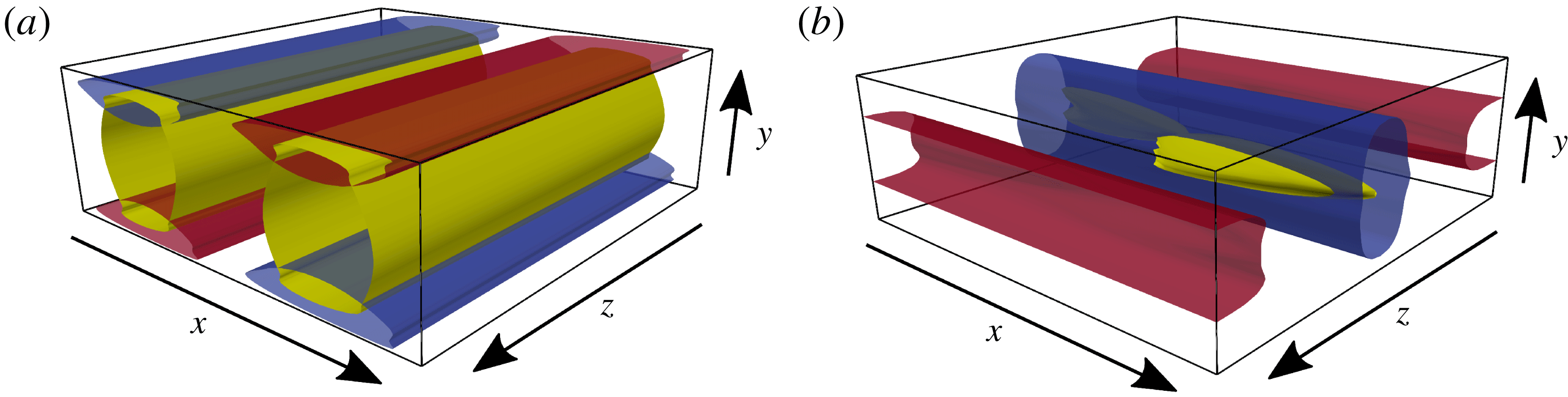
Figure 1. The exact coherent states for the transition to turbulence in plane Poiseuille flow. (a) Visualization of the Tollmien–Schlichting wave
![]() $TW_{TS}$
. The yellow surface indicates values of
$TW_{TS}$
. The yellow surface indicates values of
![]() $0.3Q_{max}$
for the
$0.3Q_{max}$
for the
![]() $Q$
-vortex criterion. The red and blue surfaces correspond to
$Q$
-vortex criterion. The red and blue surfaces correspond to
![]() $u=\pm 0.5u_{max}$
, respectively. (b) Visualization of the edge state
$u=\pm 0.5u_{max}$
, respectively. (b) Visualization of the edge state
![]() $TW_{E}$
for the bypass transition. As before, the yellow surface indicates values of
$TW_{E}$
for the bypass transition. As before, the yellow surface indicates values of
![]() $0.3Q_{max}$
for the
$0.3Q_{max}$
for the
![]() $Q$
-vortex criterion. The levels for the red and blue surfaces are now
$Q$
-vortex criterion. The levels for the red and blue surfaces are now
![]() $u=0.008$
and
$u=0.008$
and
![]() $u=-0.014$
, respectively.
$u=-0.014$
, respectively.
2 Plane Poiseuille flow and its coherent structures
To fix the geometry, let
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
be the downstream, normal and spanwise directions, and let the flow be bounded by parallel plates at
$z$
be the downstream, normal and spanwise directions, and let the flow be bounded by parallel plates at
![]() $y=\pm H$
. Dimensionless units are formed with the height
$y=\pm H$
. Dimensionless units are formed with the height
![]() $H$
and the centreline velocity
$H$
and the centreline velocity
![]() $U_{0}$
of the laminar parabolic profile so that the unit of time is
$U_{0}$
of the laminar parabolic profile so that the unit of time is
![]() $H/U_{0}$
and the Reynolds number becomes
$H/U_{0}$
and the Reynolds number becomes
![]() $Re=U_{0}H/\unicode[STIX]{x1D708}$
, with
$Re=U_{0}H/\unicode[STIX]{x1D708}$
, with
![]() $\unicode[STIX]{x1D708}$
the fluid viscosity. In these units the laminar profile becomes
$\unicode[STIX]{x1D708}$
the fluid viscosity. In these units the laminar profile becomes
![]() $\boldsymbol{u}_{0}=(1-y^{2})\boldsymbol{e}_{x}$
. The equations of motion, the incompressible Navier–Stokes equations, are solved using Channelflow (Gibson Reference Gibson2012), with a spatial resolution of
$\boldsymbol{u}_{0}=(1-y^{2})\boldsymbol{e}_{x}$
. The equations of motion, the incompressible Navier–Stokes equations, are solved using Channelflow (Gibson Reference Gibson2012), with a spatial resolution of
![]() $N_{x}=N_{z}=32$
and
$N_{x}=N_{z}=32$
and
![]() $N_{y}=65$
for a domain of length
$N_{y}=65$
for a domain of length
![]() $2\unicode[STIX]{x03C0}$
and width
$2\unicode[STIX]{x03C0}$
and width
![]() $2\unicode[STIX]{x03C0}$
and at fixed mass flux. The chosen resolution is sufficient to resolve the exact solutions and the transition process but under-resolved in the turbulent case. In the studied domain, the linear instability occurs at
$2\unicode[STIX]{x03C0}$
and at fixed mass flux. The chosen resolution is sufficient to resolve the exact solutions and the transition process but under-resolved in the turbulent case. In the studied domain, the linear instability occurs at
![]() $Re_{c}=5815$
, slightly higher than the value found by Orszag (Reference Orszag1971), on account of the slightly different domain size.
$Re_{c}=5815$
, slightly higher than the value found by Orszag (Reference Orszag1971), on account of the slightly different domain size.
The full velocity field
![]() $\boldsymbol{U}=\boldsymbol{u}_{0}+\boldsymbol{u}$
can be written as the sum of the laminar flow
$\boldsymbol{U}=\boldsymbol{u}_{0}+\boldsymbol{u}$
can be written as the sum of the laminar flow
![]() $\boldsymbol{u}_{0}$
and deviations
$\boldsymbol{u}_{0}$
and deviations
![]() $\boldsymbol{u}=(u,v,w)$
. In the following we always mean
$\boldsymbol{u}=(u,v,w)$
. In the following we always mean
![]() $\boldsymbol{u}$
when we refer to the velocity field. To characterize the size of perturbations we will use the root mean square (r.m.s.) velocity in
$\boldsymbol{u}$
when we refer to the velocity field. To characterize the size of perturbations we will use the root mean square (r.m.s.) velocity in
![]() $\boldsymbol{u}$
,
$\boldsymbol{u}$
,
or in one of the components, for example,
for the downstream component.
Tollmien–Schlichting (TS) waves are travelling waves formed by spanwise vortices. They appear in a subcritical bifurcation that extends down to
![]() $Re\approx 2610$
for a streamwise wavenumber of 1.36. The TS wave is independent of spanwise position
$Re\approx 2610$
for a streamwise wavenumber of 1.36. The TS wave is independent of spanwise position
![]() $z$
and consists of two spanwise vortices, as shown in figure 1(a).
$z$
and consists of two spanwise vortices, as shown in figure 1(a).
The Reynolds number range over which the transition to TS waves is subcritical depends on the domain size. For our domain (streamwise wavenumber of 1.0) the turning point is at
![]() $Re\approx 4685$
. A bifurcation diagram of this exact solution, referred to as
$Re\approx 4685$
. A bifurcation diagram of this exact solution, referred to as
![]() $TW_{TS}$
in the remainder of the paper, is shown in figure 2(a). The ordinate in the bifurcation diagram is the amplitude of the deviation from laminar flow (2.1). A study of the stability of the state in the full three-dimensional space shows that this lower branch state has only one unstable direction in the used computational domain for
$TW_{TS}$
in the remainder of the paper, is shown in figure 2(a). The ordinate in the bifurcation diagram is the amplitude of the deviation from laminar flow (2.1). A study of the stability of the state in the full three-dimensional space shows that this lower branch state has only one unstable direction in the used computational domain for
![]() $5727<Re<5815=Re_{c}$
. Thus, for these Reynolds numbers the state is an edge state whose stable manifold divides the state space in two parts (Skufca, Yorke & Eckhardt Reference Skufca, Yorke and Eckhardt2006). For lower
$5727<Re<5815=Re_{c}$
. Thus, for these Reynolds numbers the state is an edge state whose stable manifold divides the state space in two parts (Skufca, Yorke & Eckhardt Reference Skufca, Yorke and Eckhardt2006). For lower
![]() $Re$
, there are secondary bifurcations that add more unstable directions to the state. Specifically, near the turning point at
$Re$
, there are secondary bifurcations that add more unstable directions to the state. Specifically, near the turning point at
![]() $Re=4690$
, the lower branch has acquired approximately 350 unstable directions. Because of the high critical Reynolds numbers this state cannot explain the transition to turbulence observed in experiments at Reynolds numbers around 1000 (Carlson et al.
Reference Carlson, Widnall and Peeters1982; Nishioka & Asai Reference Nishioka and Asai1985; Lemoult et al.
Reference Lemoult, Aider and Wesfreid2012; Lemoult, Aider & Wesfreid Reference Lemoult, Aider and Wesfreid2013) or even lower (Sano & Tamai Reference Sano and Tamai2016).
$Re=4690$
, the lower branch has acquired approximately 350 unstable directions. Because of the high critical Reynolds numbers this state cannot explain the transition to turbulence observed in experiments at Reynolds numbers around 1000 (Carlson et al.
Reference Carlson, Widnall and Peeters1982; Nishioka & Asai Reference Nishioka and Asai1985; Lemoult et al.
Reference Lemoult, Aider and Wesfreid2012; Lemoult, Aider & Wesfreid Reference Lemoult, Aider and Wesfreid2013) or even lower (Sano & Tamai Reference Sano and Tamai2016).
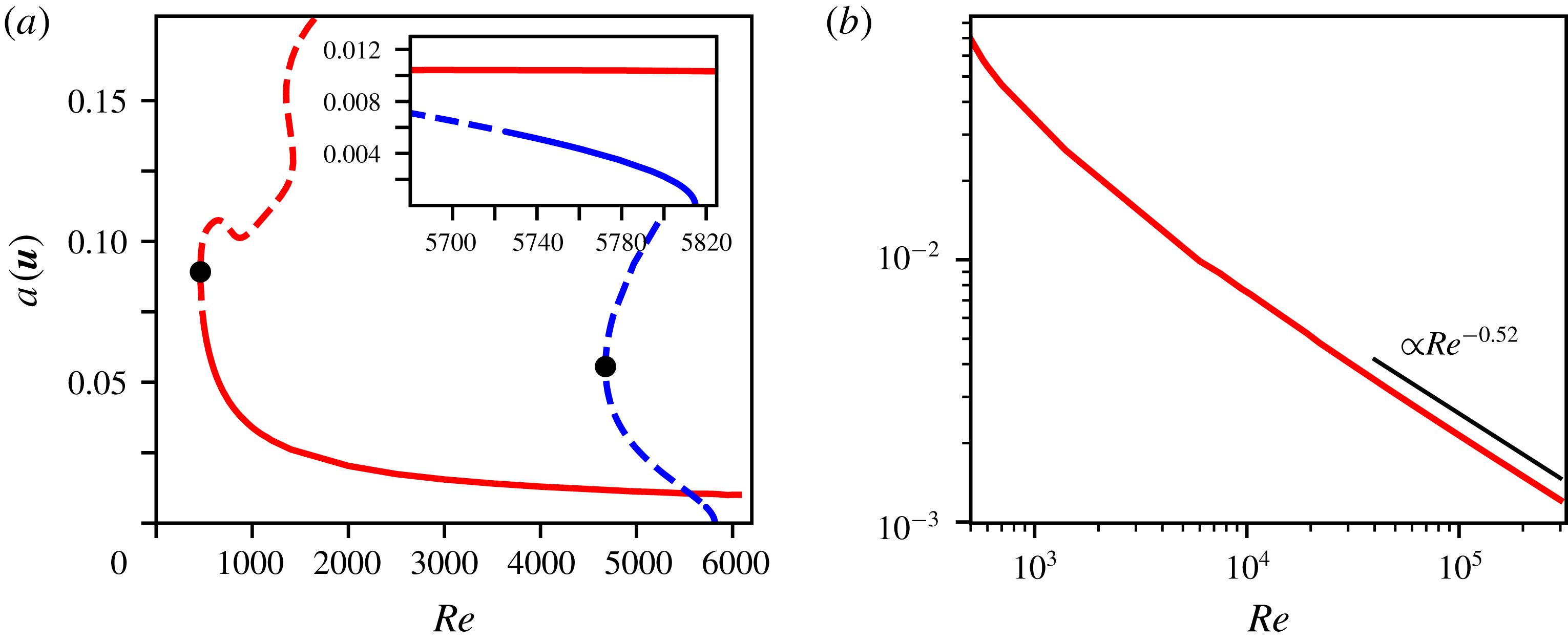
Figure 2. The bifurcation diagrams for
![]() $TW_{E}$
(red) and
$TW_{E}$
(red) and
![]() $TW_{TS}$
(blue) are shown in (a). A solid line is used if the travelling wave has just one unstable eigenvalue, while a dashed line is used when the wave has further unstable eigenvalues. The inset zooms in on the region where both waves have only one unstable eigenvalue. The bifurcation points of the waves are marked with black dots. In (b) the amplitude
$TW_{TS}$
(blue) are shown in (a). A solid line is used if the travelling wave has just one unstable eigenvalue, while a dashed line is used when the wave has further unstable eigenvalues. The inset zooms in on the region where both waves have only one unstable eigenvalue. The bifurcation points of the waves are marked with black dots. In (b) the amplitude
![]() $a(\boldsymbol{u})$
of
$a(\boldsymbol{u})$
of
![]() $TW_{E}$
is shown in a double-logarithmic plot, together with a power-law decay like
$TW_{E}$
is shown in a double-logarithmic plot, together with a power-law decay like
![]() $Re^{-0.52}$
for large
$Re^{-0.52}$
for large
![]() $Re$
.
$Re$
.
The states that are relevant to the bypass transition can be found using the method of edge tracking (Toh & Itano Reference Toh and Itano2003; Schneider, Eckhardt & Yorke Reference Schneider, Eckhardt and Yorke2007; Schneider et al.
Reference Schneider, Gibson, Lagha, De Lillo and Eckhardt2008). Starting from an arbitrary turbulent initial condition at
![]() $Re=1400$
, trajectories in the laminar–turbulent boundary that are followed with the edge-tracking algorithm converge to a travelling wave (Zammert & Eckhardt Reference Zammert and Eckhardt2014), which we referred to as
$Re=1400$
, trajectories in the laminar–turbulent boundary that are followed with the edge-tracking algorithm converge to a travelling wave (Zammert & Eckhardt Reference Zammert and Eckhardt2014), which we referred to as
![]() $TW_{E}$
in the following. After its initial identification, the state can be tracked easily to higher Reynolds numbers. The visualization in figure 1(b) shows that this state has a strong narrow upstream streak, a weaker but more extended downstream streak, and streamwise vortices. Moreover,
$TW_{E}$
in the following. After its initial identification, the state can be tracked easily to higher Reynolds numbers. The visualization in figure 1(b) shows that this state has a strong narrow upstream streak, a weaker but more extended downstream streak, and streamwise vortices. Moreover,
![]() $TW_{E}$
has a wall-normal reflection symmetry
$TW_{E}$
has a wall-normal reflection symmetry
a shift-and-reflect symmetry
and exists for a wide range in Reynolds numbers. It is created in a saddle-node bifurcation near
![]() $Re\approx 459$
(see the bifurcation diagram in figure 2
a); for other combinations of spanwise and streamwise wavelengths the state appears at an even lower Reynolds numbers of 319 (Zammert & Eckhardt Reference Zammert and Eckhardt2017).
$Re\approx 459$
(see the bifurcation diagram in figure 2
a); for other combinations of spanwise and streamwise wavelengths the state appears at an even lower Reynolds numbers of 319 (Zammert & Eckhardt Reference Zammert and Eckhardt2017).
The corresponding lower branch state can be continued to Reynolds numbers far above
![]() $3\times 10^{5}$
, and its amplitude decreases with increasing Reynolds number, as shown in figure 2(b). A fit to the amplitude for large Reynolds numbers gives a scaling like
$3\times 10^{5}$
, and its amplitude decreases with increasing Reynolds number, as shown in figure 2(b). A fit to the amplitude for large Reynolds numbers gives a scaling like
![]() $Re^{-0.52}$
, similar to that of the solution embedded in the edge of plane Couette flow (Itano et al.
Reference Itano, Akinaga, Generalis and Sugihara-Seki2013). A stability analysis of the lower branch of
$Re^{-0.52}$
, similar to that of the solution embedded in the edge of plane Couette flow (Itano et al.
Reference Itano, Akinaga, Generalis and Sugihara-Seki2013). A stability analysis of the lower branch of
![]() $TW_{E}$
shows that the travelling wave has one unstable eigenvalue for
$TW_{E}$
shows that the travelling wave has one unstable eigenvalue for
![]() $510<Re<5850$
. Therefore,
$510<Re<5850$
. Therefore,
![]() $TW_{E}$
is a second travelling wave with a stable manifold that can divide the state space into two disconnected parts. How the two edge states interact and divide up the state space will be discussed in § 3.
$TW_{E}$
is a second travelling wave with a stable manifold that can divide the state space into two disconnected parts. How the two edge states interact and divide up the state space will be discussed in § 3.
At
![]() $Re=510$
the lower branch undergoes a supercritical pitchfork bifurcation that breaks the
$Re=510$
the lower branch undergoes a supercritical pitchfork bifurcation that breaks the
![]() $s_{y}$
symmetry and adds a second unstable eigenvalue for
$s_{y}$
symmetry and adds a second unstable eigenvalue for
![]() $Re<510$
. The upper branch of the travelling wave has three unstable eigenvalues for
$Re<510$
. The upper branch of the travelling wave has three unstable eigenvalues for
![]() $Re<1000$
. Investigation of different systems which show subcritical turbulence revealed that bifurcations of exact solutions connected to the edge state of the system lead to the formation of a chaotic saddle that shows transient turbulence with exponential distributed lifetimes (Kreilos & Eckhardt Reference Kreilos and Eckhardt2012; Ritter, Mellibovsky & Avila Reference Ritter, Mellibovsky and Avila2016). In the present systems the formation of chaotic saddles cannot be studied in detail since it takes place in an unstable subspace. However, previous investigations in a symmetry-restricted system did show that the states follow such a sequence of bifurcations to the formation of a chaotic saddle (Zammert & Eckhardt Reference Zammert and Eckhardt2015, Reference Zammert and Eckhardt2017), so that we expect that also the states in the unstable subspace follow this phenomenology.
$Re<1000$
. Investigation of different systems which show subcritical turbulence revealed that bifurcations of exact solutions connected to the edge state of the system lead to the formation of a chaotic saddle that shows transient turbulence with exponential distributed lifetimes (Kreilos & Eckhardt Reference Kreilos and Eckhardt2012; Ritter, Mellibovsky & Avila Reference Ritter, Mellibovsky and Avila2016). In the present systems the formation of chaotic saddles cannot be studied in detail since it takes place in an unstable subspace. However, previous investigations in a symmetry-restricted system did show that the states follow such a sequence of bifurcations to the formation of a chaotic saddle (Zammert & Eckhardt Reference Zammert and Eckhardt2015, Reference Zammert and Eckhardt2017), so that we expect that also the states in the unstable subspace follow this phenomenology.
The edge state
![]() $TW_{E}$
discussed here is not identical to the travelling waves identified by Waleffe (Reference Waleffe2001) or Nagata & Deguchi (Reference Nagata and Deguchi2013), as they appear at considerably higher Reynolds numbers (even for their optimal wavenumbers) and are not edge states of the system.
$TW_{E}$
discussed here is not identical to the travelling waves identified by Waleffe (Reference Waleffe2001) or Nagata & Deguchi (Reference Nagata and Deguchi2013), as they appear at considerably higher Reynolds numbers (even for their optimal wavenumbers) and are not edge states of the system.
The two travelling waves described above are clearly related to the two different transition mechanisms that exist in the flow. For Reynolds numbers below the linear instability (here,
![]() $Re_{c}=5815$
), initial conditions that start close to
$Re_{c}=5815$
), initial conditions that start close to
![]() $TW_{E}$
in the state space will either decay or become turbulent without showing any approach to a TS wave: they will follow the bypass transition to turbulence. Initial conditions that start close to
$TW_{E}$
in the state space will either decay or become turbulent without showing any approach to a TS wave: they will follow the bypass transition to turbulence. Initial conditions that start close to
![]() $TW_{TS}$
can also either decay or swing up to turbulence, but they will first form TS waves. Above
$TW_{TS}$
can also either decay or swing up to turbulence, but they will first form TS waves. Above
![]() $Re_{c}$
all initial conditions will show a transition to turbulence, but it will still be possible to distinguish whether they follow the bypass or TS route to turbulence, as we will see.
$Re_{c}$
all initial conditions will show a transition to turbulence, but it will still be possible to distinguish whether they follow the bypass or TS route to turbulence, as we will see.
3 State space structure
In order to explore the arrangement of the different routes to turbulence in the space of initial conditions we pick initial conditions and integrate them until the flow either becomes turbulent or until it returns to the laminar profile. The initial conditions are taken in a two-dimensional slice of the high-dimensional space, spanned by two flow fields
![]() $\boldsymbol{u}_{1}$
and
$\boldsymbol{u}_{1}$
and
![]() $\boldsymbol{u}_{2}$
. The choice of the flow fields allows one to explore different cross-sections of state space. For the most part, we will use
$\boldsymbol{u}_{2}$
. The choice of the flow fields allows one to explore different cross-sections of state space. For the most part, we will use
![]() $\boldsymbol{u}_{1}$
and
$\boldsymbol{u}_{1}$
and
![]() $\boldsymbol{u}_{2}$
to be the travelling waves
$\boldsymbol{u}_{2}$
to be the travelling waves
![]() $TW_{E}$
and
$TW_{E}$
and
![]() $TW_{TS}$
, so that both states are part of the cross-section. The initial conditions are then parametrized by a mixing parameter
$TW_{TS}$
, so that both states are part of the cross-section. The initial conditions are then parametrized by a mixing parameter
![]() $\unicode[STIX]{x1D6FC}$
and an amplitude
$\unicode[STIX]{x1D6FC}$
and an amplitude
![]() $A$
, i.e.,
$A$
, i.e.,
For
![]() $\unicode[STIX]{x1D6FC}=0$
one explores the state space along velocity field
$\unicode[STIX]{x1D6FC}=0$
one explores the state space along velocity field
![]() $\boldsymbol{u}_{1}$
and for
$\boldsymbol{u}_{1}$
and for
![]() $\unicode[STIX]{x1D6FC}=1$
along velocity field
$\unicode[STIX]{x1D6FC}=1$
along velocity field
![]() $\boldsymbol{u}_{2}$
. If the upper and lower branch of
$\boldsymbol{u}_{2}$
. If the upper and lower branch of
![]() $TW_{E}$
are used to span such a slice, one finds that the regions in initial conditions that become turbulent have shapes that are similar to the ones in plane Couette flow (Kreilos & Eckhardt Reference Kreilos and Eckhardt2012; Zammert & Eckhardt Reference Zammert and Eckhardt2015).
$TW_{E}$
are used to span such a slice, one finds that the regions in initial conditions that become turbulent have shapes that are similar to the ones in plane Couette flow (Kreilos & Eckhardt Reference Kreilos and Eckhardt2012; Zammert & Eckhardt Reference Zammert and Eckhardt2015).

Figure 3. Visualizations of the velocity fields for perturbations with parameter
![]() $\unicode[STIX]{x1D6FC}=0.2$
, 0.4, 0.6 and 0.8 (a–d, respectively) at Reynolds number 5720. The states are scaled to have an amplitude
$\unicode[STIX]{x1D6FC}=0.2$
, 0.4, 0.6 and 0.8 (a–d, respectively) at Reynolds number 5720. The states are scaled to have an amplitude
![]() $A$
of 0.0105. The visualizations use iso-contours of the
$A$
of 0.0105. The visualizations use iso-contours of the
![]() $Q$
-vortex criterion for
$Q$
-vortex criterion for
![]() $Q=2\times 10^{-5}$
, shown in yellow. In addition, iso-surfaces for the streamwise velocity
$Q=2\times 10^{-5}$
, shown in yellow. In addition, iso-surfaces for the streamwise velocity
![]() $u=0.002$
and
$u=0.002$
and
![]() $u=-0.01$
are shown in red and blue, respectively.
$u=-0.01$
are shown in red and blue, respectively.

Figure 4. (a) Turbulence intensities
![]() $Tu$
and r.m.s.-velocities
$Tu$
and r.m.s.-velocities
![]() $\langle u\rangle$
,
$\langle u\rangle$
,
![]() $\langle v\rangle$
and
$\langle v\rangle$
and
![]() $\langle w\rangle$
and (b) mean profiles for the initial fields shown in figure 3 for different parameters
$\langle w\rangle$
and (b) mean profiles for the initial fields shown in figure 3 for different parameters
![]() $\unicode[STIX]{x1D6FC}$
at Reynolds number 5720, and turbulence intensity
$\unicode[STIX]{x1D6FC}$
at Reynolds number 5720, and turbulence intensity
![]() $Tu$
(red) in dependence on
$Tu$
(red) in dependence on
![]() $\unicode[STIX]{x1D6FC}$
. The streamwise, wall-normal and spanwise components are shown in blue, green and yellow, respectively. For
$\unicode[STIX]{x1D6FC}$
. The streamwise, wall-normal and spanwise components are shown in blue, green and yellow, respectively. For
![]() $\unicode[STIX]{x1D6FC}=0$
the contribution of the wall-normal component does not vanish but is only of order
$\unicode[STIX]{x1D6FC}=0$
the contribution of the wall-normal component does not vanish but is only of order
![]() $10^{-5}$
. (b) Mean streamwise velocity profiles (deviation from laminar) for different values of
$10^{-5}$
. (b) Mean streamwise velocity profiles (deviation from laminar) for different values of
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.

Figure 5. Two-dimensional slices of the state space for various Reynolds numbers. In (a–e), where
![]() $Re<Re_{c}=5815$
, the parameter
$Re<Re_{c}=5815$
, the parameter
![]() $\unicode[STIX]{x1D6FC}$
interpolates between the flow fields of both travelling waves, and both are indicated by white dots in the figures. In (f), where
$\unicode[STIX]{x1D6FC}$
interpolates between the flow fields of both travelling waves, and both are indicated by white dots in the figures. In (f), where
![]() $Re>Re_{c}$
the plane is spanned by the flow field of
$Re>Re_{c}$
the plane is spanned by the flow field of
![]() $TW_{E}$
and by the unstable TS mode of the laminar state. In all panels the colour indicates the time it takes to reach the turbulent states, up to a maximum integration time of 70 000 time units. Accordingly, initial conditions that do not become turbulent or return to the laminar state are indicated by dark blue. In (f) the dashed white line indicates the stable manifold of
$TW_{E}$
and by the unstable TS mode of the laminar state. In all panels the colour indicates the time it takes to reach the turbulent states, up to a maximum integration time of 70 000 time units. Accordingly, initial conditions that do not become turbulent or return to the laminar state are indicated by dark blue. In (f) the dashed white line indicates the stable manifold of
![]() $TW_{E}$
. The coloured triangles and dots in (d) mark initial conditions whose time evolution is shown in figure 6.
$TW_{E}$
. The coloured triangles and dots in (d) mark initial conditions whose time evolution is shown in figure 6.
Lower branch states are on the boundary between laminar flow and turbulence, so we begin by exploring the slice spanned by the lower branches of
![]() $TW_{E}$
and
$TW_{E}$
and
![]() $TW_{TS}$
. In figure 3, visualization for different values of
$TW_{TS}$
. In figure 3, visualization for different values of
![]() $\unicode[STIX]{x1D6FC}$
are shown. The plots illustrate how the topology of the initial flow state changes from a state dominated by streamwise streaks and vortices to a state where streaks and vortices are aligned perpendicular to the flow direction. As quantitative measures of the states, we use the r.m.s. velocity (2.2) of the individual velocity components, and the turbulent intensity
$\unicode[STIX]{x1D6FC}$
are shown. The plots illustrate how the topology of the initial flow state changes from a state dominated by streamwise streaks and vortices to a state where streaks and vortices are aligned perpendicular to the flow direction. As quantitative measures of the states, we use the r.m.s. velocity (2.2) of the individual velocity components, and the turbulent intensity
Figure 4(a) shows the dependence of these quantities on
![]() $\unicode[STIX]{x1D6FC}$
. For small values of
$\unicode[STIX]{x1D6FC}$
. For small values of
![]() $\unicode[STIX]{x1D6FC}$
the contribution of the streamwise component is much stronger than that of the other components, due to the strong low-speed streak contained in
$\unicode[STIX]{x1D6FC}$
the contribution of the streamwise component is much stronger than that of the other components, due to the strong low-speed streak contained in
![]() $TW_{E}$
. With increasing
$TW_{E}$
. With increasing
![]() $\unicode[STIX]{x1D6FC}$
the relative contribution of the wall-normal component becomes larger until for
$\unicode[STIX]{x1D6FC}$
the relative contribution of the wall-normal component becomes larger until for
![]() $\unicode[STIX]{x1D6FC}=1$
, where we have pure spanwise rolls, it is nearly as strong as the streamwise component. In figure 4(b), streamwise velocity profiles for different
$\unicode[STIX]{x1D6FC}=1$
, where we have pure spanwise rolls, it is nearly as strong as the streamwise component. In figure 4(b), streamwise velocity profiles for different
![]() $\unicode[STIX]{x1D6FC}$
are shown. For low
$\unicode[STIX]{x1D6FC}$
are shown. For low
![]() $\unicode[STIX]{x1D6FC}$
there is a pronounced minimum in the centre of the channel, which is related to the low-speed streak of
$\unicode[STIX]{x1D6FC}$
there is a pronounced minimum in the centre of the channel, which is related to the low-speed streak of
![]() $TW_{E}$
, and there are maxima close to the wall. When
$TW_{E}$
, and there are maxima close to the wall. When
![]() $\unicode[STIX]{x1D6FC}$
is increased the profile becomes nearly inverted. For large values of
$\unicode[STIX]{x1D6FC}$
is increased the profile becomes nearly inverted. For large values of
![]() $\unicode[STIX]{x1D6FC}$
there is a maximum in the centre of the channel, and minima close to the walls.
$\unicode[STIX]{x1D6FC}$
there is a maximum in the centre of the channel, and minima close to the walls.
We assign to each initial condition the time it takes to become turbulent, with an upper cutoff for initial conditions that either take longer or that never become turbulent because they return to the laminar profile. Colour-coded transition-time plots are shown in figure 5(a–e) for different Reynolds numbers below
![]() $Re_{c}$
. The boundary between initial conditions that relaminarize and those that become turbulent stands out clearly. They are formed by the stable manifold of the states and their crossings with the cross-section. The part of the laminar–turbulent boundary connected with
$Re_{c}$
. The boundary between initial conditions that relaminarize and those that become turbulent stands out clearly. They are formed by the stable manifold of the states and their crossings with the cross-section. The part of the laminar–turbulent boundary connected with
![]() $TW_{E}$
can be distinguished from that connected with
$TW_{E}$
can be distinguished from that connected with
![]() $TW_{TS}$
by the huge differences in transition times: for
$TW_{TS}$
by the huge differences in transition times: for
![]() $TW_{TS}$
, transition times are significantly longer and even exceed
$TW_{TS}$
, transition times are significantly longer and even exceed
![]() $2\times 10^{4}$
time units. The slow growth rates of TS waves has been known for a long time. An stability analysis of the base profile shows that there is an optimal Reynolds number around
$2\times 10^{4}$
time units. The slow growth rates of TS waves has been known for a long time. An stability analysis of the base profile shows that there is an optimal Reynolds number around
![]() $Re=40.000$
for which the largest growth rate is obtained. But even for this Reynolds number a growth by only a factor of 10 within 300 viscous time units is achieved (Bayly, Orszag & Herbert Reference Bayly, Orszag and Herbert1988).
$Re=40.000$
for which the largest growth rate is obtained. But even for this Reynolds number a growth by only a factor of 10 within 300 viscous time units is achieved (Bayly, Orszag & Herbert Reference Bayly, Orszag and Herbert1988).
The interaction between the two domains is rather intricate. For Reynolds number 5780, shown in figure 5(d), it seems that the borders do not cross, but rather wind around each other in a spiral shape down to very small scales. Although the wave
![]() $TW_{TS}$
has still only one unstable eigenvalue, the size of the structure that is directly connected to
$TW_{TS}$
has still only one unstable eigenvalue, the size of the structure that is directly connected to
![]() $TW_{TS}$
shrinks with decreasing
$TW_{TS}$
shrinks with decreasing
![]() $Re$
and is not visible in this kind of projection for
$Re$
and is not visible in this kind of projection for
![]() $Re<5727$
, where
$Re<5727$
, where
![]() $TW_{TS}$
has more than one unstable eigenvalue. In particular, a zoom of the area around
$TW_{TS}$
has more than one unstable eigenvalue. In particular, a zoom of the area around
![]() $TW_{TS}$
for
$TW_{TS}$
for
![]() $Re=5720$
, which is included as an inset in figure 5(a), shows that initial conditions which pass near
$Re=5720$
, which is included as an inset in figure 5(a), shows that initial conditions which pass near
![]() $TW_{TS}$
appear for
$TW_{TS}$
appear for
![]() $\unicode[STIX]{x1D6FC}=1$
only. Thus, the number of initial conditions in this projection that undergoes TS transition is of measure zero.
$\unicode[STIX]{x1D6FC}=1$
only. Thus, the number of initial conditions in this projection that undergoes TS transition is of measure zero.
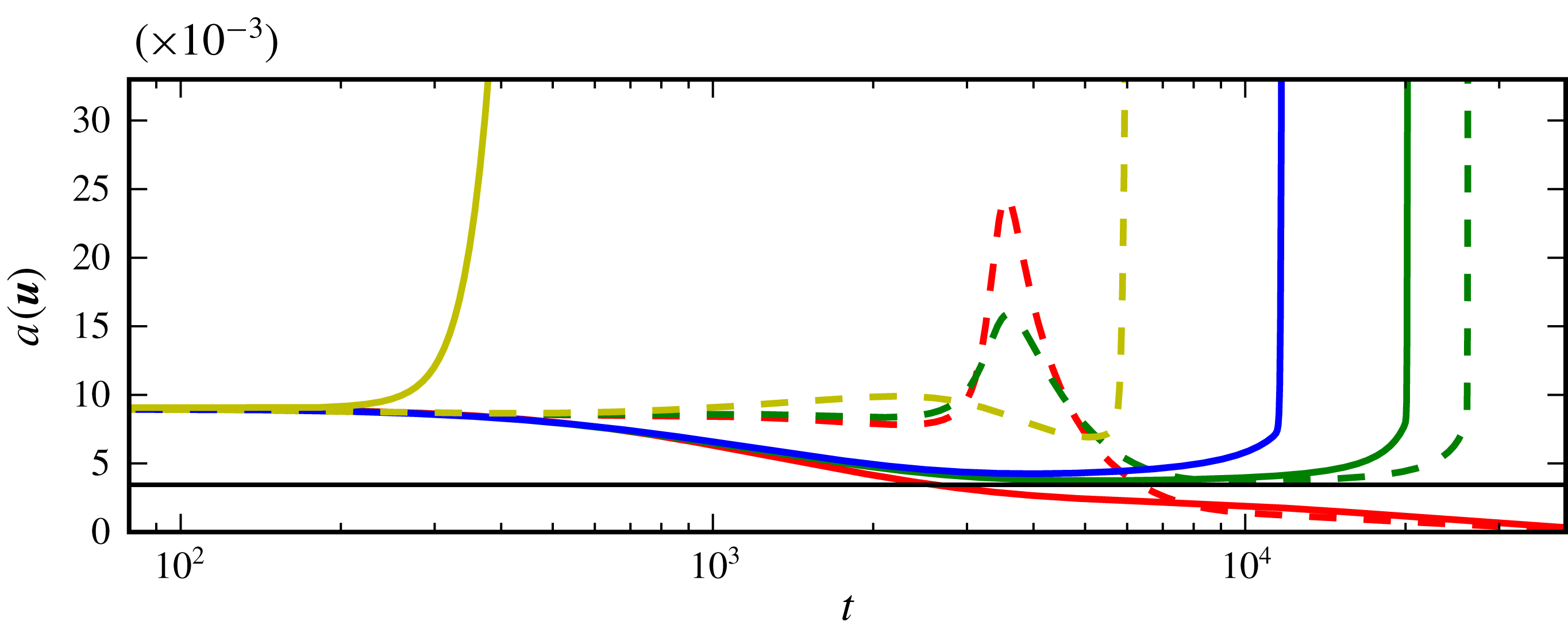
Figure 6. Time evolution of the velocity amplitude
![]() $a(\boldsymbol{u})$
for the initial conditions marked in figure 5(d) for
$a(\boldsymbol{u})$
for the initial conditions marked in figure 5(d) for
![]() $Re=5780$
. The initial conditions for the trajectories drawn with solid and dashed lines are marked in figure 5(b) with triangles and circles, respectively. The black line indicates the amplitude of the lower branch of the TS state
$Re=5780$
. The initial conditions for the trajectories drawn with solid and dashed lines are marked in figure 5(b) with triangles and circles, respectively. The black line indicates the amplitude of the lower branch of the TS state
![]() $TW_{TS}$
at
$TW_{TS}$
at
![]() $Re=5780$
. Some of the initial conditions that miss the bypass transition become turbulent nevertheless, because they are captured by the TS instability (for example, the full blue, and both green lines).
$Re=5780$
. Some of the initial conditions that miss the bypass transition become turbulent nevertheless, because they are captured by the TS instability (for example, the full blue, and both green lines).
In figure 6 the evolution of the amplitude for different initial conditions marked in figure 5(d) is shown. The green and blue lines are typical representatives of the slow TS transition. Starting with a three-dimensional initial condition, their amplitude decays and the two-dimensional TS wave
![]() $TW_{TS}$
, whose amplitude is marked by the black line, is approached.
$TW_{TS}$
, whose amplitude is marked by the black line, is approached.
Afterwards, they depart from
![]() $TW_{TS}$
again, which is a slow process because of the small growth rate. As commonly known, the transition in the case of the TS transition is eventually caused by secondary instabilities of the TS waves (Herbert Reference Herbert1988).
$TW_{TS}$
again, which is a slow process because of the small growth rate. As commonly known, the transition in the case of the TS transition is eventually caused by secondary instabilities of the TS waves (Herbert Reference Herbert1988).
The solid yellow line in figure 6 is an initial condition that undergoes bypass transition. It quickly swings up to higher amplitudes and does not approach the TS wave on its way to turbulence. The dashed yellow line is of an intermediate type. It takes a long time to become turbulent but it does not come very close to the TS wave. The relation between time evolution, transient amplification and final state is complicated and non-intuitive. For instance, the dashed red and green trajectories share a transient increase near
![]() $t\approx 4000$
, but differ in their final state: the red curve, with the higher maximum, eventually returns to the laminar profile, but the green curve, with the smaller maximum, approaches the TS level and eventually becomes turbulent following the TS route. Similarly, the red, blue and green continuous lines start with high amplitude slightly below the threshold for the bypass route. They all decay, but while the red initial conditions ends up on the decaying side of the TS wave, the green and blue cases eventually become turbulent via the TS route.
$t\approx 4000$
, but differ in their final state: the red curve, with the higher maximum, eventually returns to the laminar profile, but the green curve, with the smaller maximum, approaches the TS level and eventually becomes turbulent following the TS route. Similarly, the red, blue and green continuous lines start with high amplitude slightly below the threshold for the bypass route. They all decay, but while the red initial conditions ends up on the decaying side of the TS wave, the green and blue cases eventually become turbulent via the TS route.
For plane Couette flow it was found that a small chaotic saddle can appear inside of existing larger ones (Kreilos et al.
Reference Kreilos, Eckhardt and Schneider2014). There, trajectories that escape from the inner saddle are still captured by the outer saddle and thus they cannot decay directly. There is evidence that the appearance of TS transition in PPF follows a comparable but slightly different mechanism. At Reynolds number lower than 1000, the chaotic saddle related to bypass transition is created and subcritical turbulence exists. With increasing Reynolds number the chaotic saddle gets partly enclosed by the stable manifold of the TS wave, which above
![]() $Re=5727$
can separate two parts of the state space and therefore prevent trajectories in the interior from becoming laminar.
$Re=5727$
can separate two parts of the state space and therefore prevent trajectories in the interior from becoming laminar.
With increasing Reynolds number the number of initial conditions becoming turbulent increases. Finally, for
![]() $Re>Re_{c}$
, initial conditions that return to the laminar state no longer exist. Nevertheless, also in this supercritical regime a sudden change in the type of transition can be identified: when the amplitude increases and crosses the stable manifold of
$Re>Re_{c}$
, initial conditions that return to the laminar state no longer exist. Nevertheless, also in this supercritical regime a sudden change in the type of transition can be identified: when the amplitude increases and crosses the stable manifold of
![]() $TW_{E}$
, the transition time drops dramatically and turbulence is reached via the bypass route. In the state space visualization for
$TW_{E}$
, the transition time drops dramatically and turbulence is reached via the bypass route. In the state space visualization for
![]() $Re=5855$
, which is shown in figure 5(f), the change of the transition type presents itself in the rapid drop of the transition time with increasing
$Re=5855$
, which is shown in figure 5(f), the change of the transition type presents itself in the rapid drop of the transition time with increasing
![]() $A$
for
$A$
for
![]() $\unicode[STIX]{x1D6FC}$
values between 0 and 0.6.
$\unicode[STIX]{x1D6FC}$
values between 0 and 0.6.
In the supercritical range the stable manifold of the bypass edge state
![]() $TW_{E}$
separates initial conditions undergoing the quick bypass transition from initial conditions that become turbulent by TS transition. The state space picture at a higher Reynolds number of 6000 looks qualitatively similar to the one shown in figure 5(c), including the switch from TS to bypass transition when the stable manifold of
$TW_{E}$
separates initial conditions undergoing the quick bypass transition from initial conditions that become turbulent by TS transition. The state space picture at a higher Reynolds number of 6000 looks qualitatively similar to the one shown in figure 5(c), including the switch from TS to bypass transition when the stable manifold of
![]() $TW_{E}$
is crossed.
$TW_{E}$
is crossed.
4 State space for constant pressure gradient
Up to this point all results were obtained by simulations which keep the bulk velocity constant. Since previous studies showed differences between the system operating at constant bulk velocity and at constant pressure gradient (Barkley Reference Barkley1990; Soibelman & Meron Reference Soibelman and Meiron1991), we here analyse the changes in the state space structure when forces driving the flow are changed.
If the pressure gradient is fixed the Reynolds number
![]() $Re_{P}$
can be defined by using the centreline velocity of the laminar flow corresponding to the pressure gradient, together with the half-channel width and the viscosity. In dimensionless form the pressure gradient then is given by
$Re_{P}$
can be defined by using the centreline velocity of the laminar flow corresponding to the pressure gradient, together with the half-channel width and the viscosity. In dimensionless form the pressure gradient then is given by
![]() $\text{d}P/\text{d}x=-2/Re_{P}$
. This definition ensures that for the laminar base flow, the pressure- and bulk-based Reynolds numbers coincide.
$\text{d}P/\text{d}x=-2/Re_{P}$
. This definition ensures that for the laminar base flow, the pressure- and bulk-based Reynolds numbers coincide.
We chose a Reynolds number of 5780 for a comparison of two constraints. For this Reynolds number the state space structure shows the highest complexity for the case of constant bulk velocity. Using the same parametrization of initial conditions, we obtain the transition-time plot shown in figure 7. Although there are small differences from the case of constant bulk velocity – for example, the tongue-like structure connected to
![]() $TW_{TS}$
appears to be slightly thinner – the main features are unchanged.
$TW_{TS}$
appears to be slightly thinner – the main features are unchanged.
The relative stability to a change of the operating conditions can be rationalized by the large distance to the turning points of the solution branches. Lower branch states commonly differ only slightly between pressure and bulk Reynolds number if the distance to the turning point is large. However, these differences can become huge close to the turning point of the solution branch (e.g. Zammert Reference Zammert2015, chap. 3.2).
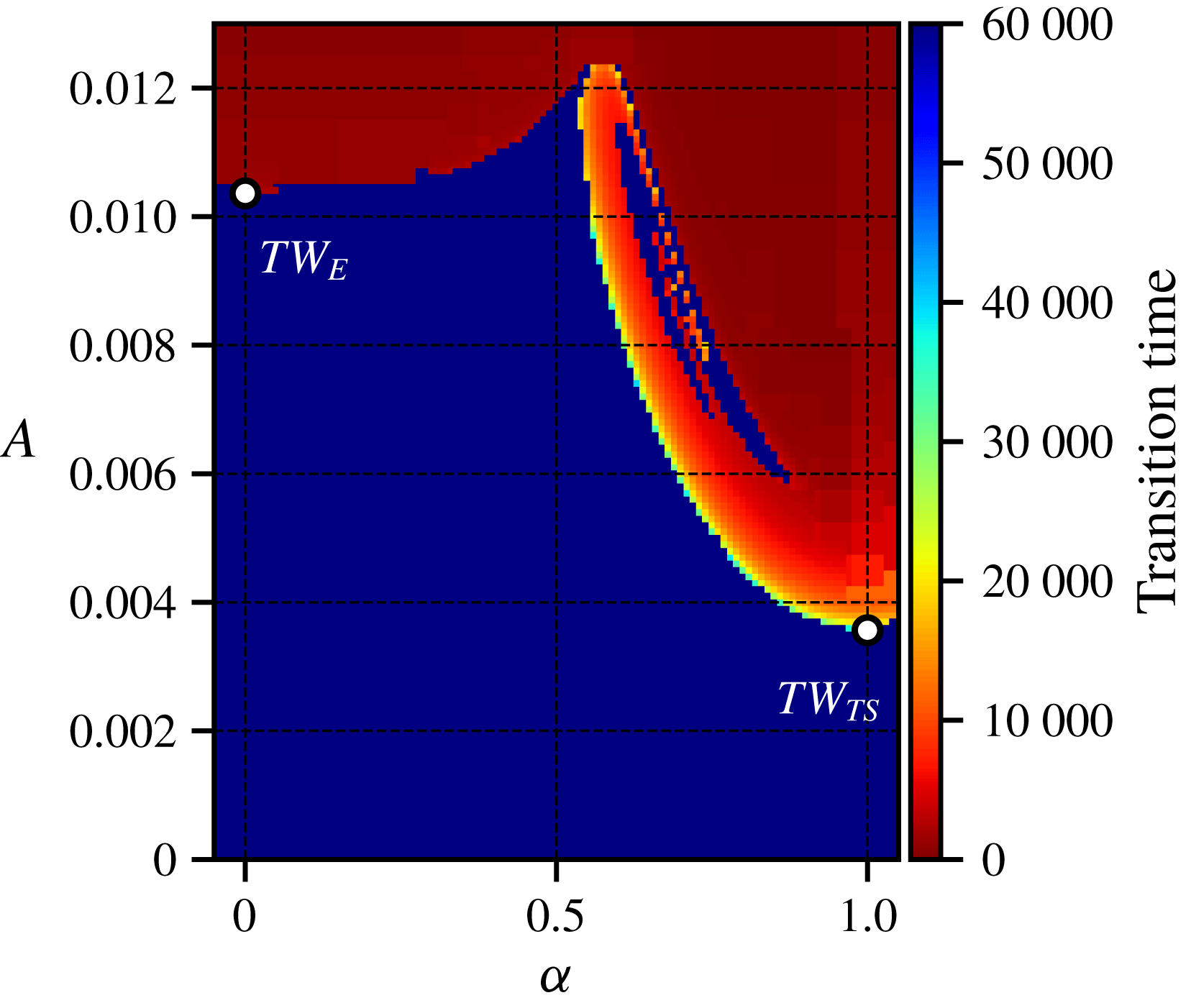
Figure 7. Two-dimensional slice of the state space for a pressure-based Reynolds number (
![]() $Re_{P}$
) of 5780.
$Re_{P}$
) of 5780.
These results show that organization of the state space depends only weakly on driving with constant pressure difference or constant bulk flow, and that the slices are similar. Furthermore, since the flow states used to generate the state space slice are also solutions for the case of constant bulk velocity, but for slightly different values of the bulk Reynolds number, the calculations suggest that the obtained state space slices are to some degree robust to small disturbances of the flow fields used to generate the slices.
5 Conclusions
We have explored the coexistence of two types of transition in subcritical plane Poiseuille flow connected with the existence of states dominated by streamwise and spanwise vortices (bypass and TS transition). Probing the state space by scanning initial conditions in two-dimensional cross-sections gave information on the sets of initial conditions that follow one or the other route to turbulence. The results show that the transition via TS waves initially occupies a tiny region of state space. As this region expands, it approaches the bypass-dominated regions, but a boundary between the two remains visible because of the very different times needed to reach turbulence. This extends to the parameter range where the laminar profile is unstable to the formation of TS waves. The investigated state
![]() $TW_{E}$
lies on the border between the two transition types also for Reynolds number far above the critical one. Since its amplitude scales approximately as
$TW_{E}$
lies on the border between the two transition types also for Reynolds number far above the critical one. Since its amplitude scales approximately as
![]() $Re^{-0.5}$
for high Reynolds numbers, the minimal threshold required to trigger bypass transition must decrease with this power or even faster.
$Re^{-0.5}$
for high Reynolds numbers, the minimal threshold required to trigger bypass transition must decrease with this power or even faster.
The results shown here are obtained for small domains, where the extensive numerical computations for very many initial conditions are feasible. For larger domains, the corresponding exact coherent structures are localized, as shown by Jiménez (Reference Jiménez1990) and Mellibovsky & Meseguer (Reference Mellibovsky and Meseguer2015) for TS waves and by Zammert & Eckhardt (Reference Zammert and Eckhardt2014) for the bypass transition. Since the bifurcation diagrams for the localized states are similar to that of the extended states, we anticipate a similar phenomenology also for localized perturbations in spatially extended states.
The methods presented here can also be used to explore the relation between bypass transition and TS waves in boundary layers (Duguet et al. Reference Duguet, Schlatter, Henningson and Eckhardt2012; Kreilos et al. Reference Kreilos, Khapko, Schlatter, Duguet, Henningson and Eckhardt2016). More generally, they can be applied to any kind of transition where two different paths compete: examples include shear-driven or convection-driven instabilities in thermal convection (Clever & Busse Reference Clever and Busse1992; Zammert, Fischer & Eckhardt Reference Zammert, Fischer and Eckhardt2016), the interaction between transitions driven by different symmetries (Faisst & Eckhardt Reference Faisst and Eckhardt2003; Wedin & Kerswell Reference Wedin and Kerswell2004; Schneider et al. Reference Schneider, Gibson, Lagha, De Lillo and Eckhardt2008), or the interaction between the established subcritical scenario and the recently discovered linear instability in Taylor–Couette flow with a rotating outer cylinder (Deguchi Reference Deguchi2017).
Acknowledgement
B.E. passed away on 7 August 2019 before finalization of the revision of this manuscript. He was a constant source of inspiring new ideas, an astute mind, a wonderful teacher and a good friend. He will be dearly missed.