Article contents
Transition to turbulence in shock-driven mixing: a Mach number study
Published online by Cambridge University Press: 21 November 2011
Abstract
Large-eddy simulations of single-shock-driven mixing suggest that, for sufficiently high incident Mach numbers, a two-gas mixing layer ultimately evolves to a late-time, fully developed turbulent flow, with Kolmogorov-like inertial subrange following a 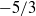 power law. After estimating the kinetic energy injected into the diffuse density layer during the initial shock–interface interaction, we propose a semi-empirical characterization of fully developed turbulence in such flows, based on scale separation, as a function of the initial parameter space, as
power law. After estimating the kinetic energy injected into the diffuse density layer during the initial shock–interface interaction, we propose a semi-empirical characterization of fully developed turbulence in such flows, based on scale separation, as a function of the initial parameter space, as 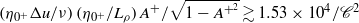 , which corresponds to late-time Taylor-scale Reynolds numbers
, which corresponds to late-time Taylor-scale Reynolds numbers 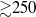 . In this expression,
. In this expression, 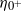 represents the post-shock perturbation amplitude,
represents the post-shock perturbation amplitude, 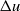 the change in interface velocity induced by the shock refraction,
the change in interface velocity induced by the shock refraction,  the characteristic kinematic viscosity of the mixture,
the characteristic kinematic viscosity of the mixture, 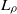 the inner diffuse thickness of the initial density profile,
the inner diffuse thickness of the initial density profile, 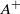 the post-shock Atwood ratio, and
the post-shock Atwood ratio, and 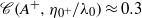 for the gas combination and post-shock perturbation amplitude considered. The initially perturbed interface separating air and SF6 (pre-shock Atwood ratio
for the gas combination and post-shock perturbation amplitude considered. The initially perturbed interface separating air and SF6 (pre-shock Atwood ratio 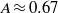 ) was impacted in a heavy–light configuration by a shock wave of Mach number
) was impacted in a heavy–light configuration by a shock wave of Mach number 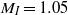 , 1.25, 1.56, 3.0 or 5.0, for which
, 1.25, 1.56, 3.0 or 5.0, for which 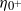 is fixed at about 25 % of the dominant wavelength
is fixed at about 25 % of the dominant wavelength 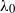 of an initial, Gaussian perturbation spectrum. Only partial isotropization of the flow (in the sense of turbulent kinetic energy and dissipation) is observed during the late-time evolution of the mixing zone. For all Mach numbers considered, the late-time flow resembles homogeneous decaying turbulence of Batchelor type, with a turbulent kinetic energy decay exponent
of an initial, Gaussian perturbation spectrum. Only partial isotropization of the flow (in the sense of turbulent kinetic energy and dissipation) is observed during the late-time evolution of the mixing zone. For all Mach numbers considered, the late-time flow resembles homogeneous decaying turbulence of Batchelor type, with a turbulent kinetic energy decay exponent 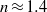 and large-scale (
and large-scale (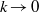 ) energy spectrum
) energy spectrum 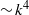 , and a molecular mixing fraction parameter,
, and a molecular mixing fraction parameter, 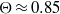 . An appropriate time scale characterizing the Taylor-scale Reynolds number decay, as well as the evolution of mixing parameters such as
. An appropriate time scale characterizing the Taylor-scale Reynolds number decay, as well as the evolution of mixing parameters such as 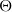 and the effective Atwood ratio
and the effective Atwood ratio 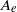 , seem to indicate the existence of low- and high-Mach-number regimes.
, seem to indicate the existence of low- and high-Mach-number regimes.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 59
- Cited by


