Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhao, Yongling
Lei, Chengwang
and
Patterson, John C.
2013.
Resonance of the thermal boundary layer adjacent to an isothermally heated vertical surface.
Journal of Fluid Mechanics,
Vol. 724,
Issue. ,
p.
305.
Xu, Feng
Patterson, John C.
and
Lei, Chengwang
2014.
An experimental study of the coupled thermal boundary layers adjacent to a partition in a differentially heated cavity.
Experimental Thermal and Fluid Science,
Vol. 54,
Issue. ,
p.
12.
Saha, Suvash C.
and
Gu, Y.T.
2014.
Transient air flow and heat transfer in a triangular enclosure with a conducting partition.
Applied Mathematical Modelling,
Vol. 38,
Issue. 15-16,
p.
3879.
XU, F.
YANG, Q.
and
YU, P.
2014.
NUMERICAL STUDIES OF TRANSITION FROM STEADY TO UNSTEADY COUPLED THERMAL BOUNDARY LAYERS.
International Journal of Computational Methods,
Vol. 11,
Issue. supp01,
p.
1344002.
Xu, Feng
2015.
Unsteady coupled thermal boundary layers induced by a fin on the partition of a differentially heated cavity.
International Communications in Heat and Mass Transfer,
Vol. 67,
Issue. ,
p.
59.
Hattori, T.
Patterson, J.C.
and
Lei, C.
2015.
Scaling and direct stability analyses of natural convection induced by absorption of solar radiation in a parallelepiped cavity.
International Journal of Thermal Sciences,
Vol. 88,
Issue. ,
p.
19.
Saha, Suvash C.
Gu, Y.T.
and
Khan, M.M.K.
2016.
Thermofluid Modeling for Energy Efficiency Applications.
p.
59.
Williamson, N.
Armfield, S.W.
Lin, Wenxian
and
Kirkpatrick, M.P.
2016.
Stability and Nusselt number scaling for inclined differentially heated cavity flow.
International Journal of Heat and Mass Transfer,
Vol. 97,
Issue. ,
p.
787.
Khatamifar, Mehdi
Lin, Wenxian
Armfield, S.W.
Holmes, David
and
Kirkpatrick, M.P.
2017.
Conjugate natural convection heat transfer in a partitioned differentially-heated square cavity.
International Communications in Heat and Mass Transfer,
Vol. 81,
Issue. ,
p.
92.
Zemani, Farah
and
Sabeur-Bendehina, Amina
2018.
Transient Natural Convection in Partitioned Enclosures.
Mechanics and Mechanical Engineering,
Vol. 22,
Issue. 4,
p.
1015.
Liu, Yang
Bian, Yongning
Zhao, Yongling
Zhang, Shuaikun
and
Suo, Qinghui
2019.
Scaling laws for the transient convective flow in a differentially and linearly heated rectangular cavity at Pr > 1.
Physics of Fluids,
Vol. 31,
Issue. 4,
Ke, Junhao
Williamson, N.
Armfield, S. W.
McBain, G. D.
and
Norris, S. E.
2019.
Stability of a temporally evolving natural convection boundary layer on an isothermal wall.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
p.
1163.
Ke, Junhao
Williamson, N.
Armfield, S. W.
Norris, S. E.
and
Komiya, A.
2020.
Law of the wall for a temporally evolving vertical natural convection boundary layer.
Journal of Fluid Mechanics,
Vol. 902,
Issue. ,
Wang, Haoyu
and
Lei, Chengwang
2020.
A numerical investigation of conjugate thermal boundary layers in a differentially heated partitioned cavity filled with different fluids.
Physics of Fluids,
Vol. 32,
Issue. 7,
Liu, Yang
2020.
Dynamics and scale analysis of the transient convective flow induced by cooling a Pr<1 fluid with linear thermal forcing.
International Journal of Heat and Mass Transfer,
Vol. 154,
Issue. ,
p.
119767.
Saha, Sumon
Barua, Sonkolon
Kushwaha, Balaram
Subedi, Sabir
Hasan, Mohammad N.
and
Saha, Suvash C.
2020.
Conjugate natural convection in a corrugated solid partitioned differentially heated square cavity.
Numerical Heat Transfer, Part A: Applications,
Vol. 78,
Issue. 10,
p.
541.
Ke, Junhao
Williamson, N.
Armfield, S.W.
Komiya, A.
and
Norris, S.E.
2021.
High Grashof number turbulent natural convection on an infinite vertical wall.
Journal of Fluid Mechanics,
Vol. 929,
Issue. ,
Khatamifar, Mehdi
Lin, Wenxian
and
Dong, Liqiang
2021.
Transient conjugate natural convection heat transfer in a differentially-heated square cavity with a partition of finite thickness and thermal conductivity.
Case Studies in Thermal Engineering,
Vol. 25,
Issue. ,
p.
100952.
Issakhov, Alibek
Sabyrkulova, Aidana
and
Abylkassymova, Aizhan
2024.
INFLUENCE OF TILT ANGLES AND DIFFERENT MODELS OF FLUID VISCOSITY ON COUPLED NATURAL CONVECTION IN A DIFFERENTIALLY HEATED CLOSED SQUARE CAVITY WITH A BAFFLE
.
p.
413.
Liu, Yang
and
Zhu, Yifeng
2024.
Instability of a vertical free convection boundary layer flow: Asymptotically from a perfectly flat one to a highly curved one.
Physical Review Fluids,
Vol. 9,
Issue. 10,
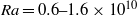 at Prandtl number
at Prandtl number 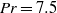 and at aspect ratios of
and at aspect ratios of 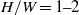 where
where 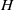 and
and 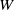 are the height and width of the cavity. It was found that the thermal coupling of the boundary layers on either side of the conducting partition causes the cavity flow to become absolutely unstable for a Rayleigh number at which otherwise similar non-partitioned cavity flow is steady but convectively unstable. Additionally, unlike the non-partitioned cavity, which eventually bifurcates to a multi-modal oscillatory regime, this bifurcation is manifested as a single mode oscillation with
are the height and width of the cavity. It was found that the thermal coupling of the boundary layers on either side of the conducting partition causes the cavity flow to become absolutely unstable for a Rayleigh number at which otherwise similar non-partitioned cavity flow is steady but convectively unstable. Additionally, unlike the non-partitioned cavity, which eventually bifurcates to a multi-modal oscillatory regime, this bifurcation is manifested as a single mode oscillation with 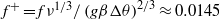 , where
, where 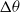 is the temperature difference between the hot and cold walls,
is the temperature difference between the hot and cold walls, 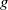 is the gravitational acceleration,
is the gravitational acceleration, 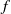 is the oscillation frequency and
is the oscillation frequency and  and
and 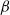 are the fluid viscosity and coefficient of thermal expansion respectively. The critical Rayleigh number for this transition occurs between
are the fluid viscosity and coefficient of thermal expansion respectively. The critical Rayleigh number for this transition occurs between 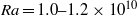 for
for 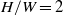 and
and 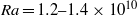 for
for 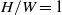 , indicating that the instability has an aspect ratio dependence.
, indicating that the instability has an aspect ratio dependence.