Hostname: page-component-f554764f5-nwwvg Total loading time: 0 Render date: 2025-04-20T16:20:57.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Transition of buoyancy-driven flow from an axisymmetric to non-axisymmetric vortex inside an evaporating sessile droplet

Published online by Cambridge University Press:  17 October 2024

Jialing Yu Open the ORCID record for Jialing Yu [Opens in a new window] ,
Zhenhai Pan Open the ORCID record for Zhenhai Pan [Opens in a new window]  and
Justin A. Weibel Open the ORCID record for Justin A. Weibel [Opens in a new window]
Jialing Yu
Affiliation:
School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China
Zhenhai Pan*
Affiliation:
School of Mechanical Engineering, Shanghai Institute of Technology, Shanghai 201418, PR China
Justin A. Weibel*
Affiliation:
School of Mechanical Engineering, Purdue University, West Lafayette, 47906 IN, USA
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

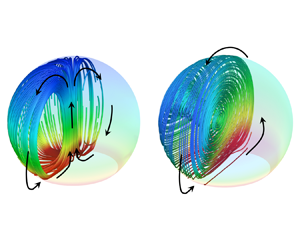
The internal flow within an evaporating sessile droplet has intriguing fluid mechanics important to various microfluidics applications. In the present study, a phenomenon is observed through numerical methods wherein the buoyancy-driven flow structure inside a droplet on a non-wetting substrate transitions from an axisymmetric toroidal vortex flow to a non-axisymmetric single vortex flow with increase in the substrate temperature. As the axisymmetric nature of the droplet flow field and evaporation characteristics are broken, the internal velocity accelerates significantly. The transition, which is attributed to a flow instability inside the droplet, is more prone to occur as the droplet volume or the contact angle increases. The onset of the flow transition is analysed as the amplification of a small perturbation, thereby establishing a correlation between the flow instability and the Rayleigh number (Ra). Specifically, when Ra exceeds some critical value, the onset of the flow transition is observed, which explains the effects of substrate temperature and droplet volume on the internal flow. Next, the influence of the droplet contact angle on the critical Ra was investigated, and the underlying reasons were analysed. Finally, we discuss the heat transfer efficiency within the droplet and analyse why the internal flow tends to transition to a non-axisymmetric flow pattern from an energy minimization perspective.

JFM classification

Convection: Buoyancy-driven instability Drops and Bubbles: Drops Phase change: Condensation/evaporation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 997 , 25 October 2024 , A47
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bennacer, R. & Sefiane, K. 2014 Vortices, dissipation and flow transition in volatile binary drops. J. Fluid Mech. 749, 649–665.CrossRefGoogle Scholar
Brutin, D. & Sefiane, K. 2022 Drying of Complex Fluid Drops: Fundamentals and Applications, vol. 14. Royal Society of Chemistry.CrossRefGoogle Scholar
Brutin, D., Sobac, B., Loquet, B. & Sampol, J. 2010 Pattern formation in drying drops of blood. J. Fluid Mech. 667, 85–95.CrossRefGoogle Scholar
Brutin, D. & Starov, V. 2018 Recent advances in droplet wetting and evaporation. Chem. Soc. Rev. 47 (2), 558–585.CrossRefGoogle Scholar
Carle, F., Semenov, S., Medale, M & Brutin, D. 2016 Contribution of convective transport to evaporation of sessile droplets: empirical model. Intl J. Therm. Sci. 101, 35–47.CrossRefGoogle Scholar
Carle, F., Sobac, B. & Brutin, D. 2012 Hydrothermal waves on ethanol droplets evaporating under terrestrial and reduced gravity levels. J. Fluid Mech. 712, 614–623.CrossRefGoogle Scholar
Cazabat, A.-M. & Guéna, G. 2010 Evaporation of macroscopic sessile droplets. Soft Matt. 6 (12), 2591–2612.CrossRefGoogle Scholar
Chandramohan, A., Dash, S., Weibel, J.A., Chen, X.M. & Garimella, S.V. 2016 Marangoni convection in evaporating organic liquid droplets on a nonwetting substrate. Langmuir 32 (19), 4729–4735.CrossRefGoogle Scholar
Chong, K.L. & Xia, K.-Q. 2016 Exploring the severely confined regime in Rayleigh–Bénard convection. J. Fluid Mech. 805, R4.CrossRefGoogle Scholar
Chong, K.L., Yang, Y., Huang, S.D., Zhong, J.Q., Stevens, R., Verzicco, R., Lohse, D. & Xia, K.Q. 2017 Confined Rayleigh–Benard, rotating Rayleigh–Benard, and double diffusive convection: a unifying view on turbulent transport enhancement through coherent structure manipulation. Phys. Rev. Lett. 119 (6), 064501.CrossRefGoogle Scholar
Dash, S., Chandramohan, A., Weibel, J.A. & Garimella, S.V. 2014 Buoyancy-induced on-the-spot mixing in droplets evaporating on nonwetting surfaces. Phys. Rev. E 90 (6), 062407.CrossRefGoogle Scholar
Dash, S. & Garimella, S.V. 2014 Droplet evaporation on heated hydrophobic and superhydrophobic surfaces. Phys. Rev. E 89 (4), 042402.CrossRefGoogle Scholar
Deegan, R.D., Bakajin, O., Dupont, T.F., Huber, G., Nagel, S.R. & Witten, T.A. 1997 Capillary flow as the cause of ring stains from dried liquid drops. Nature 389 (6653), 827–829.CrossRefGoogle Scholar
Diddens, C. 2017 Detailed finite element method modeling of evaporating multi-component droplets. J. Comput. Phys. 340, 670–687.CrossRefGoogle Scholar
Diddens, C., Li, Y.X. & Lohse, D. 2021 Competing Marangoni and Rayleigh convection in evaporating binary droplets. J. Fluid Mech. 914, A23.CrossRefGoogle Scholar
Dietrich, E., Wildeman, S., Visser, C.W., Hofhuis, K., Kooij, E., Stefan, Z., Harold, J.W. & Lohse, D. 2016 Role of natural convection in the dissolution of sessile droplets. J. Fluid Mech. 794, 45–67.CrossRefGoogle Scholar
Edwards, A.M.J., Atkinson, P.S., Cheung, C.S., Liang, H., Fairhurst, D.J. & Ouali, F.F. 2018 Density-driven flows in evaporating binary liquid droplets. Phys. Rev. Lett. 121 (18), 184501.CrossRefGoogle Scholar
van Gaalen, R.T., Wijshoff, H.M.A., Kuerten, J.G.M. & Diddens, C. 2022 Competition between thermal and surfactant-induced Marangoni flow in evaporating sessile droplets. J. Colloid Interface Sci. 622, 892–903.CrossRefGoogle Scholar
Gelderblom, H., Diddens, C. & Marin, A. 2022 Evaporation-driven liquid flow in sessile droplets. Soft Matt. 18 (45), 8535–8553.CrossRefGoogle Scholar
Hu, H. & Larson, R.G. 2005 Analysis of the effects of Marangoni stresses on the microflow in an evaporating sessile droplet. Langmuir 21 (9), 3972–3980.CrossRefGoogle Scholar
Hu, H. & Larson, R.G. 2006 Marangoni effect reverses coffee-ring depositions. J. Phys. Chem. B 110 (14), 7090–7094.CrossRefGoogle Scholar
Josyula, T., Mahapatra, P.S. & Pattamatta, A. 2022 Internal flow in evaporating water drops: dominance of Marangoni flow. Exp. Fluids 63 (2), 49.CrossRefGoogle Scholar
Kang, K.H., Leel, S.J., Lee, C.M. & Kang, I.S. 2004 Quantitative visualization of flow inside an evaporating droplet using the ray tracing method. Meas. Sci. Technol. 15 (6), 1104–1112.CrossRefGoogle Scholar
Li, Y.X., Diddens, C., Lv, P.Y., Wijshoff, H., Versluis, M. & Lohse, D. 2019 Gravitational effect in evaporating binary microdroplets. Phys. Rev. Lett. 122 (11), 114501.CrossRefGoogle Scholar
Linstrom, P.J. & Mallard, W.G. (Eds) 2023 NIST Chemistry WebBook, NIST Standard Reference Database Number 69. https://webbook.nist.gov/, National Institute of Standards and Technology.Google Scholar
Liu, H., Zeng, Z., Qiu, Z. & Yin, L. 2021 Linear stability analysis of Rayleigh–Bénard convection for cold water near its density maximum in a cylindrical container. Intl J. Heat Mass Transfer 173, 121240.CrossRefGoogle Scholar
Marangoni, C. 1865 Sull'espansione delle goccie d'un liquido galleggianti sulla superfice di altro liquido. Fratelli Fusi.Google Scholar
Masoudi, S. & Kuhlmann, H.C. 2017 Axisymmetric buoyant–thermocapillary flow in sessile and hanging droplets. J. Fluid Mech. 826, 1066–1095.CrossRefGoogle Scholar
Miele, E., Accardo, A., Falqui, A., Marini, M., Giugni, A., Leoncini, M., De Angelis, F., Krahne, R. & Di Fabrizio, E. 2015 Writing and functionalisation of suspended dna nanowires on superhydrophobic pillar arrays. Small 11 (1), 134–140.CrossRefGoogle Scholar
Nguyen, V.X. & Stebe, K.J. 2002 Patterning of small particles by a surfactant-enhanced Marangoni-Benard instability. Phys. Rev. Lett. 88 (16), 164501.CrossRefGoogle Scholar
Pan, Z. & Wang, H. 2013 Bénard–Marangoni instability on evaporating menisci in capillary channels. Intl J. Heat Mass Transfer 63, 239–248.CrossRefGoogle Scholar
Pan, Z.H., Dash, S., Weibel, J.A. & Garimella, S.V. 2013 Assessment of water droplet evaporation mechanisms on hydrophobic and superhydrophobic substrates. Langmuir 29 (51), 15831–15841.CrossRefGoogle Scholar
Pan, Z.H., Weibel, J.A. & Garimella, S.V. 2020 Transport mechanisms during water droplet evaporation on heated substrates of different wettability. Intl J. Heat Mass Transfer 152, 119524.CrossRefGoogle Scholar
Sáenz, P.J., Sefiane, K., Kim, J., Matar, O.K. & Valluri, P. 2015 Evaporation of sessile drops: a three-dimensional approach. J. Fluid Mech. 772, 705–739.CrossRefGoogle Scholar
Savino, R., Paterna, D. & Favaloro, N. 2002 Buoyancy and Marangoni effects in an evaporating drop. J. Thermophys. Heat Transfer 16 (4), 562–574.CrossRefGoogle Scholar
Sefiane, K., Christy, J.R.E., Duursma, G., Ebeling, J.C., Seewald, T. & Harmand, S. 2022 Flow and heat measurement within self-rewetting mixtures of 1-pentanol and water drops. Intl J. Therm. Sci. 176, 107532.CrossRefGoogle Scholar
Shen, L., Ren, J.H. & Duan, F. 2022 Linking nonisothermal interfacial temperature and flow field measurements at an evaporating droplet. Intl J. Heat Mass Transfer 183, 122141.CrossRefGoogle Scholar
Sobac, B. & Brutin, D. 2012 Thermocapillary instabilities in an evaporating drop deposited onto a heated substrate. Phys. Fluids 24 (3), 032103.CrossRefGoogle Scholar
Squires, T.M. & Quake, S.R. 2005 Microfluidics: fluid physics at the nanoliter scale. Rev. Mod. Phys. 77 (3), 977–1026.CrossRefGoogle Scholar
Tam, D., von Arnim, V., McKinley, G.H. & Hosoi, A.E. 2009 Marangoni convection in droplets on superhydrophobic surfaces. J. Fluid Mech. 624, 101–123.CrossRefGoogle Scholar
Thomson, J. 1855 XLII. On certain curious motions observable at the surfaces of wine and other alcoholic liquors. Lond. Edinb. Dubl. Phil. Mag. J. Sci. 10 (67), 330–333.CrossRefGoogle Scholar
Trouette, B., Chenier, E., Doumenc, F., Delcarte, C. & Guerrier, B. 2012 Transient Rayleigh–Benard-Marangoni solutal convection. Phys. Fluids 24 (7), 074108.CrossRefGoogle Scholar
Wang, D., Jiang, H., Liu, S., Zhu, X. & Sun, C. 2021 Effects of radius ratio on annular centrifugal Rayleigh–Bénard convection. J. Fluid Mech. 930, A19.CrossRefGoogle Scholar
Wang, Q., Verzicco, R., Lohse, D. & Shishkina, O. 2020 Multiple states in turbulent large-aspect-ratio thermal convection: what determines the number of convection rolls? Phys. Rev. Lett. 125 (7), 074501.CrossRefGoogle Scholar
Wanschura, M., Kuhlmann, H.C. & Rath, H.J. 1996 Three-dimensional instability of axisymmetric buoyant convection in cylinders heated from below. J. Fluid Mech. 326, 399–415.CrossRefGoogle Scholar
Wen, J.T., Ho, C.M. & Lillehoj, P.B. 2013 Coffee ring aptasensor for rapid protein detection. Langmuir 29 (26), 8440–8446.CrossRefGoogle Scholar
Wilson, S.K. & D'Ambrosio, H.-M. 2023 Evaporation of sessile droplets. Annu. Rev. Fluid Mech. 55 (1), 481–509.CrossRefGoogle Scholar
Yang, R., Chong, K.L., Wang, Q., Verzicco, R., Shishkina, O. & Lohse, D. 2020 Periodically modulated thermal convection. Phys. Rev. Lett. 125 (15), 154502.CrossRefGoogle Scholar
Yim, E., Bouillant, A. & Gallaire, F. 2021 Buoyancy-driven convection of droplets on hot nonwetting surfaces. Phys. Rev. E 103 (5), 053105.CrossRefGoogle Scholar
Zhu, J.L. & Shi, W.Y. 2021 Hydrothermal waves in sessile droplets evaporating at a constant contact angle mode. Intl J. Heat Mass Transfer 172, 121131.CrossRefGoogle Scholar
Zhu, J.L., Shi, W.Y. & Feng, L. 2019 Benard-Marangoni instability in sessile droplet evaporating at constant contact angle mode on heated substrate. Intl J. Heat Mass Transfer 134, 784–795.CrossRefGoogle Scholar
Supplementary material: File

Yu et al. supplementary movie

Transition Process of Internal Flow Patterns from Axisymmetric to Non-Axisymmetric in an Evaporating Sessile Droplet
Download Yu et al. supplementary movie(File)
File 9.9 MB