Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T13:19:53.787Z Has data issue: false hasContentIssue false
  • English
  • Français

Transient ventilation dynamics induced by heat sources of unequal strength

Published online by Cambridge University Press:  02 December 2013

Ajay B. Shrinivas  and
Gary R. Hunt
Ajay B. Shrinivas
Affiliation:
Department of Civil and Environmental Engineering, Imperial College London, London SW7 2AZ, UK
Gary R. Hunt*
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine theoretically the transient displacement flow and density stratification that develops within a ventilated box after two localized floor-level heat sources of unequal strengths are activated. The heat input is represented by two non-interacting turbulent axisymmetric plumes of constant buoyancy fluxes 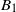${B}_{1} $ and 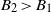${B}_{2} \gt {B}_{1} $. The box connects to an unbounded quiescent external environment of uniform density via openings at the top and base. A theoretical model is developed to predict the time evolution of the dimensionless depths 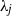${\lambda }_{j} $ and mean buoyancies 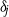${\delta }_{j} $ of the ‘intermediate’ 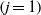$(j= 1)$ and ‘top’ 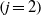$(j= 2)$ layers leading to steady state. The flow behaviour is classified in terms of a stratification parameter 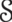, a dimensionless measure of the relative forcing strengths of the two buoyant layers that drive the flow. We find that 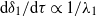$\mathrm{d} {\delta }_{1} / \mathrm{d} \tau \propto 1/ {\lambda }_{1} $ and 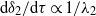$\mathrm{d} {\delta }_{2} / \mathrm{d} \tau \propto 1/ {\lambda }_{2} $, where $\tau $ is a dimensionless time. When 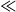$\hspace{0.167em} \hspace{0.167em} \ll \hspace{0.167em} \hspace{0.167em} $1, the intermediate layer is shallow (small 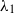${\lambda }_{1} $), whereas the top layer is relatively deep (large 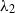${\lambda }_{2} $) and, in this limit, 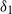${\delta }_{1} $ and 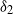${\delta }_{2} $ evolve on two characteristically different time scales. This produces a time lag and gives rise to a ‘thermal overshoot’, during which 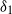${\delta }_{1} $ exceeds its steady value and attains a maximum during the transients; a flow feature we refer to, in the context of a ventilated room, as ‘localized overheating’. For a given source strength ratio 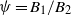$\psi = {B}_{1} / {B}_{2} $, we show that thermal overshoots are realized for dimensionless opening areas 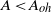$A\lt {A}_{oh} $ and are strongly dependent on the time history of the flow. We establish the region of 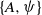$\{ A, \psi \} $ space where rapid development of 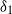${\delta }_{1} $ results in 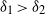${\delta }_{1} \gt {\delta }_{2} $, giving rise to a bulk overturning of the buoyant layers. Finally, some implications of these results, specifically to the ventilation of a room, are discussed.

JFM classification

Convection: Convection Convection: Plumes/thermals Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 738 , 10 January 2014 , pp. 34 - 64
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baines, W. D. 1975 Entrainment by a plume or jet at a density interface. J. Fluid Mech. 68, 309–320.Google Scholar
Baines, W. D. & Turner, J. S. 1969 Turbulent buoyant convection from a source in a confined region. J. Fluid Mech. 37, 51–80.Google Scholar
Barnett, J. S. 1991 The dynamics of buoyant releases in confined spaces. PhD thesis, DAMTP, University of Cambridge.Google Scholar
Bower, D. J., Caulfield, C. P., Fitzgerald, S. D. & Woods, A. W. 2008 Transient ventilation dynamics following a change in strength of a point source of heat. J. Fluid Mech. 614, 15–37.Google Scholar
Coomaraswamy, I. A. & Caulfield, C. P. 2011 Time-dependent ventilation flows driven by opposing wind and buoyancy. J. Fluid Mech. 672, 33–59.CrossRefGoogle Scholar
Cooper, P. & Linden, P. F. 1996 Natural ventilation of an enclosure containing two buoyancy sources. J. Fluid Mech. 311, 153–176.Google Scholar
Economidou, M. & Hunt, G. R. 2010 Transient flows in enclosures: a generalized approach for modelling the effects of geometry, heat gains and wind. Build. Environ. 45, 2607–2619.Google Scholar
Flynn, M. R. & Caulfield, C. P. 2006 Natural ventilation in interconnected chambers. J. Fluid Mech. 564, 139–158.Google Scholar
Holford, J. M. & Woods, A. W. 2007 On the thermal buffering of naturally ventilated buildings through internal thermal mass. J. Fluid Mech. 580, 3–29.Google Scholar
Hughes, G. O. & Griffiths, R. W. 2008 Horizontal convection. Annu. Rev. Fluid Mech. 40, 185–208.Google Scholar
Hunt, G. R. & Coffey, C. J. 2010 Emptying boxes – classifying transient natural ventilation flows. J. Fluid Mech. 646, 137–168.Google Scholar
Hunt, G. R. & Linden, P. F. 1998 Time-dependent displacement ventilation caused by variations in internal heat gains: application to a lecture theatre. In Proc. ROOMVENT ’98, the 6th Intl Conf. on Air Distribution in Rooms, Stockholm, Sweden (ed. Mundt, E. & Malmstrom, T. G.), pp. 203–210. KTH Stockholm.Google Scholar
Hunt, G. R. & Linden, P. F. 2001 Steady-state flows in an enclosure ventilated by buoyancy forces assisted by wind. J. Fluid Mech. 426, 355–386.Google Scholar
Kaye, N. B. & Hunt, G. R. 2004 Time-dependent flows in an emptying filling box. J. Fluid Mech. 520, 135–156.Google Scholar
Kaye, N. B. & Hunt, G. R. 2006 Weak fountains. J. Fluid Mech. 558, 319–328.Google Scholar
Kaye, N. B. & Hunt, G. R. 2007 Overturning in a filling box. J. Fluid Mech. 576, 297–323.Google Scholar
Kumagai, M. 1984 Turbulent buoyant convection from a source in a confined two-layered region. J. Fluid Mech. 147, 105–131.CrossRefGoogle Scholar
Lane-Serff, G. F. & Sandbach, S. D. 2012 Emptying non-adiabatic filling boxes: the effects of heat transfers on the fluid dynamics of natural ventilation. J. Fluid Mech. 701, 386–406.CrossRefGoogle Scholar
Lin, Y. J. P. & Linden, P. F. 2005 The entrainment due to a turbulent fountain at a density interface. J. Fluid Mech. 542, 25–52.CrossRefGoogle Scholar
Linden, P. F. & Cooper, P. 1996 Multiple sources of buoyancy in a naturally ventilated enclosure. J. Fluid Mech. 311, 177–192.Google Scholar
Linden, P. F., Lane-Serff, G. F. & Smeed, D. A. 1990 Emptying filling boxes: the fluid mechanics of natural ventilation. J. Fluid Mech. 212, 309–335.Google Scholar
Morton, B. R., Taylor, G. & Turner, J. S. 1956 Turbulent buoyant convection from a source in a confined region. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Scase, M. M., Caulfield, C. P., Dalziel, S. B. & Hunt, J. C. R. 2006 Time-dependent plumes and jets with decreasing source strengths. J. Fluid Mech. 563, 443–461.Google Scholar
Turner, J. S. 1986 Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 173, 431–471.Google Scholar
Wagner, A., Klebe, M. & Parker, C. 2007 Monitoring results of a naturally ventilated and passively cooled office building in Frankfurt, Germany. Intl J. Ventilation 6, 3–20.Google Scholar
Wong, A. B. D. & Griffiths, R. W. 1999 Stratification and convection produced by multiple turbulent plumes. Dyn. Atmos. Oceans 30, 101–123.Google Scholar
Wong, A. B. D., Griffiths, R. W. & Hughes, G. O. 2001 Shear layers driven by turbulent plumes. J. Fluid Mech. 434, 209–241.Google Scholar