Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T17:09:05.610Z Has data issue: false hasContentIssue false
  • English
  • Français

Transient nonlinear microrheology in hydrodynamically interacting colloidal dispersions: flow cessation

Published online by Cambridge University Press:  09 December 2019

Ritesh P. Mohanty  and
Roseanna N. Zia Open the ORCID record for Roseanna N. Zia [Opens in a new window]
Ritesh P. Mohanty
Affiliation:
Department of Chemical Engineering, Stanford University, Stanford, CA94305, USA
Roseanna N. Zia*
Affiliation:
Department of Chemical Engineering, Stanford University, Stanford, CA94305, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

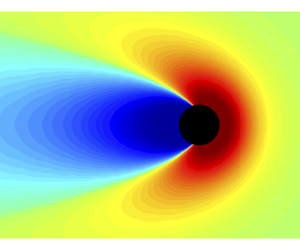
Relaxation of a colloidal dispersion following flow shutoff occurs over distinct time scales, providing a useful method for identifying microscopic forces that are otherwise difficult to detect. Active microrheology facilitates such interrogation for small-scale systems such as biological cells, where a Brownian probe is driven by an external force through the dispersion and its motion is tracked to infer flow properties. An interplay between external forces, Brownian motion, hydrodynamic interactions and interparticle forces deforms the microstructure surrounding the probe, which alters probe speed. Application of the Stokes drag law relates mean probe speed to the effective viscosity of the embedding medium. We present a micromechanical theoretical model for this relationship during nonlinear transient relaxation upon removal of the external force. Upon cessation, contributions to viscosity linear in the force vanish instantly, but hydrodynamics influences subsequent relaxation, as well as the pre-cessation structure that sets the initial condition. Stronger pre-cessation flow drives faster relaxation of both structure and rheology. Non-equilibrium entropic contributions persist after shutoff, decaying over time. Hydrodynamic interactions slow this relaxation by hindering relative Brownian and interparticle displacements. The dissipation of entropically stored energy produces a deterministic force that drives deterministic probe motion even after the external force is removed, giving a natural connection to the chemical potential. Using this idea, we show that probe back-travel gives a direct measure of the osmotic pressure and the time scale over which entropically stored energy is dissipated. Modelling a range of repulsions provides a platform for particle formulation tuned to desired transient response.

JFM classification

Complex Fluids: Colloids Multiphase and Particle-laden Flows: Particle/fluid flow Non-Newtonian Flows: Rheology
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , A14
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barnes, H. A. 1989 Shear-thickening (‘Dilatancy’) is suspensions of nonaggregating solid particles dispersed in Newtonian fluids. J. Rheol. 33, 329–366.CrossRefGoogle Scholar
Batchelor, G. K. 1976 Brownian diffusion of particles with hydrodynamic interaction. J. Fluid Mech. 74, 1–29.CrossRefGoogle Scholar
Batchelor, G. K. 1982 Sedimentation in a dilute polydisperse system of interacting spheres. Part 1. General theory. J. Fluid Mech. 119, 379–408.CrossRefGoogle Scholar
Bausch, A. R., Ziemann, F., Boulbitch, A. A., Jacobson, K. & Sackmann, E. 1998 Local measurements of viscoelastic parameters of adherent cell surfaces by magnetic bead rheometry. Biophys. J. 75, 2038–2049.CrossRefGoogle Scholar
Bedeaux, D. 1987 The effective viscosity for a suspension of spheres. J. Colloid Interface Sci. 118, 80–86.CrossRefGoogle Scholar
Bender, J. & Wagner, N. J. 1995 Optical measurement of the contributions of colloidal forces to the rheology of concentrated suspensions. J. Colloid Interface Sci. 172, 171–184.CrossRefGoogle Scholar
Bergenholtz, J., Brady, J. F. & Vicic, M. 2002 The non-Newtonian rheology of dilute colloidal suspensions. J. Fluid Mech. 456, 239–275.CrossRefGoogle Scholar
Bouchaud, J.-P. 2008 Anomalous relaxation in complex systems: from stretched to compressed exponentials. In Anomalous Transport: Foundations and Applications, Wiley-VCH.Google Scholar
Brady, J. F. 1993 The rheological behavior of concentrated colloidal dispersions. J. Chem. Phys. 99 (1), 567–581.CrossRefGoogle Scholar
Brady, J. F. 1994 Brownian motion, hydrodynamics, and the osmotic pressure. J. Fluid Mech. 272 (4), 3335–3341.Google Scholar
Brady, J. F. & Bossis, G. 1985 The rheology of concentrated suspensions of spheres in simple shear flow by numerical simulation. J. Fluid Mech. 155, 105–129.CrossRefGoogle Scholar
Brady, J. F. & Morris, J. F. 1997 Microstructure of strongly sheared suspensions and its impact on rheology and diffusion. J. Fluid Mech. 348, 103–139.CrossRefGoogle Scholar
Carpen, I. C. & Brady, J. F. 2005 Microrheology of colloidal dispersions by Brownian dynamics simulations. J. Rheol. 49, 1483–1502.CrossRefGoogle Scholar
Chu, H. C. W. & Zia, R. N. 2016 Active microrheology of hydrodynamically interacting colloids: normal stresses and entropic energy density. J. Rheol. 60, 755–781.CrossRefGoogle Scholar
Chu, H. C. W. & Zia, R. N. 2017 The non-Newtonian rheology of hydrodynamically interacting colloids via active, nonlinear microrheology. J. Rheol. 61, 551–574.CrossRefGoogle Scholar
Chu, H. C. W. & Zia, R. N. 2019 Toward a non-equilibrium Stokes-Einstein relation in colloidal dispersions. J. Colloid Interface Sci. 539, 388–399.CrossRefGoogle Scholar
Crocker, J. C. 1997 Measurement of the hydrodynamic corrections to the brownian motion of two colloidal spheres. J. Chem. Phys. 106, 2837–2840.CrossRefGoogle Scholar
Crocker, J. C., Matteo, J. A., Dinsmore, A. D. & Yodh, A. 1999 Entropic attraction and repulsion in binary colloids probed with a line optical tweezer. Phys. Rev. Lett. 82, 4352–4355.CrossRefGoogle Scholar
Crocker, J. C., Valentine, M. T., Weeks, E. R., Gisler, T., Kaplan, P. D., Yodh, A. G. & Weitz, D. A. 2000 Two-point microrheology of inhomogeneous soft materials. Phys. Rev. Lett. 85, 888–891.CrossRefGoogle ScholarPubMed
Davis, R. H. & Hill, N. A. 1992 Hydrodynamic diffusion of a sphere sedimenting through a dilute suspension of neutrally buoyant spheres. J. Fluid Mech. 236, 513–533.CrossRefGoogle Scholar
DePuit, R. J. & Squires, T. M. 2012 Micro-macro-discrepancies in nonlinear microrheology: I. Quantifying mechanisms in a suspension of Brownian ellipsoids. J. Phys.: Condens. Matter 24, 464106 (1–11).Google Scholar
D’Haene, P., Mewis, J. & Fuller, G. 1993 Scattering dichroism measurements of flow-induced structure of a shear thickening suspension. J. Colloid Interface Sci. 156, 350–358.CrossRefGoogle Scholar
Dolata, B. E. & Zia, R. N. 2018 Non-equilibrium pair interactions in colloidal dispersions. J. Fluid Mech. 836, 694–739.CrossRefGoogle Scholar
Foss, D. R.1999 Rheological behavior of colloidal suspensions: the effects of hydrodynamic interactions. PhD thesis, California Institute of Technology, Pasadena, CA.Google Scholar
Foss, D. R. & Brady, J. F. 2000a Brownian Dynamics simulation of hard-sphere colloidal dispersions. J. Rheol. 44, 629–651.CrossRefGoogle Scholar
Foss, D. R. & Brady, J. F. 2000b Structure, diffusion and rheology of Brownian suspensions by Stokesian dynamics simulation. J. Fluid Mech. 407, 167–200.CrossRefGoogle Scholar
Freundlich, H. & Sfifriz, W. 1923 Über die Elastizität von Solen und Gelen. Z. Phys. Chem. 104, 223–261.Google Scholar
Furst, E. M. 2005 Applications of laser tweezers in complex fluid rheology. Curr. Opin. Colloid Interface Sci. 10, 79–86.CrossRefGoogle Scholar
Gazuz, I., Puertas, A. M., Voigtmann, T. & Fuchs, M. 2009 Active and nonlinear microrheology in dense colloidal suspensions. Phys. Rev. Lett. 102, 248302.CrossRefGoogle ScholarPubMed
Gisler, T. & Weitz, D. A. 1998 Tracer microrheology in complex fluids. Curr. Opin. Colloid Interface Sci. 3, 586–592.CrossRefGoogle Scholar
Gisler, T. & Weitz, D. A. 1999 Scaling of the microrheology of semidilute F-actin solutions. Phys. Rev. Lett. 82, 1606–1610.CrossRefGoogle Scholar
Gnann, M. V., Gazuz, I., Puertas, A. M., Fuchs, M. & Voigtmann, T. 2011 Schematic models for active nonlinear microrheology. Soft Matt. 7, 1390–1396.CrossRefGoogle Scholar
Gomez-Solano, J. R. & Bechinger, C. 2015 Transient dynamics of a colloidal particle driven through a viscoelastic fluid. New J. Phys. 17, 103032.CrossRefGoogle Scholar
Guilford, W. H., Lantz, R. C. & Gore, R. W. 1995 Locomotive forces produced by single leukocytes in vivo and in vitro. Am. J. Physiol. Cell. Physiol. 268 (5), C1308–C1312.CrossRefGoogle ScholarPubMed
Habdas, P., Schaar, D., Levitt, A. C. & Weeks, E. R. 2004 Forced motion of a probe particle near the colloidal glass transition. Eur. Phys. Lett. 67, 477–483.CrossRefGoogle Scholar
Hoh, N. J.2013 Effects of particle size ratio on single particle motion in colloidal dispersions. PhD thesis, California Institute of Technology, Pasadena, CA.Google Scholar
Hoh, N. J. & Zia, R. N. 2015 Hydrodynamic diffusion in active microrheology of non-colloidal suspension: the role of interparticle forces. J. Fluid Mech. 785, 189–218.CrossRefGoogle Scholar
Hoh, N. J. & Zia, R. N. 2016a Force-induced diffusion in suspensions of hydrodynamically interacting colloids. J. Fluid Mech. 795, 739–783.CrossRefGoogle Scholar
Hoh, N. J. & Zia, R. N. 2016b The impact of probe size on measurements of diffusion in active microrheology. Lab on a Chip 16, 3114–3129.CrossRefGoogle Scholar
Huang, D. E. & Zia, R. N. 2019 Sticky, active microrheology. Part 1. Linear-response. J. Colloid Interface Sci. 554, 580–591.CrossRefGoogle ScholarPubMed
Jeffrey, D. J. & Onishi, Y. 1984 Calculation of the resistance and mobility functions of two unequal rigid spheres in low-Reynolds-number flow. J. Fluid Mech. 139, 261–290.CrossRefGoogle Scholar
Kaffashi, B., O’Brien, V. T., Mackay, M. E. & Underwood, S. M. 1997 Elastic-like and viscous-like components of the shear viscosity for nearly hard sphere, Brownian suspensions. J. Colloid Interface Sci. 187, 22–28.CrossRefGoogle ScholarPubMed
Khair, A. S. & Brady, J. F. 2005 ‘Microviscoelasticity’ of colloidal dispersions. J. Rheol. 49 (6), 1449–1481.CrossRefGoogle Scholar
Khair, A. S. & Brady, J. F. 2006 Single particle motion in colloidal dispersions: a simple model for active and nonlinear microrheology. J. Fluid Mech. 557, 73–117.CrossRefGoogle Scholar
Khair, A. S. & Brady, J. F. 2007 On the motion of two particles translating with equal velocities through a colloidal diaspersion. Proc. R. Soc. Lond. A 463, 223–240.CrossRefGoogle Scholar
Khair, A. S. & Brady, J. F. 2008 Microrheology of colloidal dispersions: shape matters. J. Rheol. 52, 165–196.CrossRefGoogle Scholar
Kim, S. & Karilla, S. J. 1991 Microhydrodynamics: Principles and Selected Applications. Butterworth-Heinemann.Google Scholar
de Kruif, C. G., van Lersel, E. M. F., Vrij, A. & Russel, W. B. 1985 Hard sphere colloidal dispersions: viscosity as a function of shear rate and volume fraction. J. Chem. Phys. 83, 4717–4725.CrossRefGoogle Scholar
Landrum, B. J., Russel, W. B. & Zia, R. N. 2016 Delayed yield in colloidal gels: creep, flow, and re-entrant solid regimes. J. Rheol. 60, 783–807.CrossRefGoogle Scholar
Lau, A. W. C., Hoffman, B. D., Davies, A., Crocker, J. C. & Lubensky, T. C. 2003 Microrheology, stress fluctuations, and active behavior of living cells. Phys. Rev. Lett. 91, 198101.CrossRefGoogle ScholarPubMed
Leitmann, S., Mandal, S., Fuchs, M., Puertas, A. M. & Franosch, T. 2018 Time-dependent active microrheology in dilute colloidal suspensions. Phys. Rev. Fluids 3, 103301.CrossRefGoogle Scholar
Levine, A. J. & Lubensky, T. C. 2000 One- and two- particle microrheology. Phys. Rev. Lett. 85, 1774–1778.CrossRefGoogle ScholarPubMed
Lionberger, R. A. & Russel, W. B. 1994 High frequency modulus of hard sphere colloids. J. Rheol. 38 (6), 1885–1908.CrossRefGoogle Scholar
Mackay, M. E. & Kaffashi, B. 1995 Stress jumps of charged colloidal suspensions, measurement of the elastic-like and viscous-like stress components. J. Colloid Interface Sci. 174, 117–123.CrossRefGoogle Scholar
Maranzano, B. J. & Wagner, N. J. 2002 Flow-small angle neutron scattering measurements of colloidal dispersion microstructure evolution through the shear thickening transition. J. Chem. Phys. 117, 10291–10302.CrossRefGoogle Scholar
Marenne, S., Morris, J., Foss, D. R. & Brady, J. F. 2017 Unsteady shear flows of colloidal hard-sphere suspensions by dynamic simulation. J. Rheol. 61, 477–501.CrossRefGoogle Scholar
Mason, T. G., Genevan, K., van Zanten, J. H., Wirtz, D. & Kuo, S. C. 1997 Particle tracking microrheology of complex fluids. Phys. Rev. Lett. 79, 3283–3285.CrossRefGoogle Scholar
Mohanty, R. P. & Zia, R. N. 2018 The impact of hydrodynamics on viscosity evolution in colloidal dispersions: transient, nonlinear microrheology. AIChE, Futures Issue 64, 3198–3214.CrossRefGoogle Scholar
Nazockdast, E. & Morris, J. F. 2016 Active microrheology of colloidal suspensions: simulation and Microstructural theory. J. Rheol. 60, 733–753.CrossRefGoogle Scholar
Russel, W. B. 1984 The Huggins coefficient as a means for characterizing suspended particles. J. Chem. Soc. Faraday Trans. 2 80, 31–41.CrossRefGoogle Scholar
Schultz, K. M. & Furst, E. M. 2011 High-throughput rheology in a microfluidic device. Lab on a Chip 11, 3802–3809.CrossRefGoogle Scholar
Shikata, T. & Pearson, D. S. 1994 Viscoelastic behavior of concentrated spherical suspensions. J. Rheol. 38 (3), 601–616.CrossRefGoogle Scholar
Squires, T. M. 2008 Nonlinear Microrheology: bulk Stresses versus Direct Interactions. Langmuir 24, 1147–1159.CrossRefGoogle ScholarPubMed
Squires, T. M. & Brady, J. F. 2005 A simple paradigm for active and nonlinear microrheology. Phys. Fluids 17 (7), 073101.CrossRefGoogle Scholar
Squires, T. M. & Mason, T. G. 2010 Fluid Mechanics of Microrheology. Annu. Rev. Fluid Mech. 42, 413–438.CrossRefGoogle Scholar
Sriram, I.2010 Active microrheology of colloidal suspensions. PhD thesis, University of Delaware.CrossRefGoogle Scholar
Sriram, I., DePuit, R., Squires, T. M. & Furst, E. M. 2009 Small amplitude active oscillatory microrheology of a colloidal suspension. J. Rheol. 53, 357–381.CrossRefGoogle Scholar
Sriram, I., Meyer, A. & Furst, E. M. 2010 Active microrheology of a colloidal suspension in the direct collision limit. Phys. Fluids 22, 062003.CrossRefGoogle Scholar
Su, Y., Swan, J. W. & Zia, R. N. 2017 Pair mobility functions for rigid spheres in concentrated colloidal dispersions: stresslet and straining motion couplings. J. Chem. Phys. 146, 124903.Google ScholarPubMed
Swan, J. W. & Zia, R. N. 2013 Active microrheology: fixed-velocity versus fixed-force. Phys. Fluids 25 (8), 083303.CrossRefGoogle Scholar
Swan, J. W., Zia, R. N. & Brady, J. F. 2014 Large amplitude oscillatory microrheology. J. Rheol. 58 (1), 1–41.CrossRefGoogle Scholar
Voigtmann, T. & Fuchs, M. 2013 Force-driven micro-rheology. The European Physical Journal Special Topics 222, 2819–2833.CrossRefGoogle Scholar
Watanabe, H., Yao, M.-L., Yamagishi, A., Osaki, K., Shitata, T., Niwa, H. & Morishima, Y. 1996 Nonlinear rheological behavior of a concentrated spherical silica suspension. Rheol. Acta 35, 433–445.CrossRefGoogle Scholar
van der Werff, J. C., de Kruif, C. G., Blom, C. & Mellema, J. 1989 Linear viscoelastic behavior of dense hard-sphere dispersions. Phys. Rev. A 39 (2), 795–807.CrossRefGoogle ScholarPubMed
Wilson, L. G., Harrison, A. W., Schfield, A. B., Arlt, J. & Poon, W. C. K. 2009 Passive and active microrheology of hard-sphere colloids. J. Phys. Chem. 113, 3806–3812.CrossRefGoogle ScholarPubMed
Wulfert, R., Seifert, U. & Speck, T. 2017 Nonequilibrium depletion interaction in active microrheology. Soft Matt. 13, 9093–9102.CrossRefGoogle Scholar
Zia, R. N. 2018 Active and passive microrheology: theory and simulation. Annu. Rev. Fluid Mech. 50, 371–405.CrossRefGoogle Scholar
Zia, R. N. & Brady, J. F. 2010 Single-particle motion in colloids: force-induced diffusion. J. Fluid Mech. 658, 188–210.CrossRefGoogle Scholar
Zia, R. N. & Brady, J. F. 2012 Microviscosity, microdiffusivity, and normal stresses in colloidal dispersions. J. Rheol. 56 (5), 1175–1208.CrossRefGoogle Scholar
Zia, R. N. & Brady, J. F. 2013 Stress development, relaxation, and memory in colloidal dispersions: transient nonlinear microrheology. J. Rheol. 57 (2), 457–492.CrossRefGoogle Scholar
Zia, R. N., Landrum, B. J. & Russel, W. B. 2014 A micro-mechanical study of coarsening and rheology of colloidal gels: cage building, cage hoping, and Smoluchowski’s ratchet. J. Rheol. 58, 1121–1157.CrossRefGoogle Scholar
Zia, R. N., Swan, J. W. & Su, Y. 2015 Pair mobility functions for rigid spheres in concentrated colloidal dispersions: force, torque, translation, and rotation. J. Chem. Phys. 143, 224901.Google ScholarPubMed
Ziemann, F., Radler, J. & Sackmann, E. 1994 Local measurements of viscoelastic moduli of entangled actin networks using an oscillating magnetic bead microrheometer. Biophys. J. 66, 2210–2216.CrossRefGoogle Scholar