Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Peñas-López, Pablo
Moreno Soto, Álvaro
Parrales, Miguel A.
van der Meer, Devaraj
Lohse, Detlef
and
Rodríguez-Rodríguez, Javier
2017.
The history effect on bubble growth and dissolution. Part 2. Experiments and simulations of a spherical bubble attached to a horizontal flat plate.
Journal of Fluid Mechanics,
Vol. 820,
Issue. ,
p.
479.
Dietrich, Erik
Rump, Maaike
Lv, Pengyu
Kooij, E. Stefan
Zandvliet, Harold J. W.
and
Lohse, Detlef
2017.
Segregation in dissolving binary-component sessile droplets.
Journal of Fluid Mechanics,
Vol. 812,
Issue. ,
p.
349.
Maheshwari, Shantanu
van der Hoef, Martin
Prosperetti, Andrea
and
Lohse, Detlef
2017.
Molecular dynamics study of multicomponent droplet dissolution in a sparingly miscible liquid.
Journal of Fluid Mechanics,
Vol. 833,
Issue. ,
p.
54.
Lohse, Detlef
2018.
Bubble puzzles: From fundamentals to applications.
Physical Review Fluids,
Vol. 3,
Issue. 11,
Enríquez, Óscar R.
Robles, Daniel
Peñas-López, Pablo
and
Rodríguez-Rodríguez, Javier
2019.
Shaky life of a water drop in an anise oil-rich environment.
Physical Review Fluids,
Vol. 4,
Issue. 10,
Tan, Huanshu
Diddens, Christian
Mohammed, Ali Akash
Li, Junyi
Versluis, Michel
Zhang, Xuehua
and
Lohse, Detlef
2019.
Microdroplet nucleation by dissolution of a multicomponent drop in a host liquid.
Journal of Fluid Mechanics,
Vol. 870,
Issue. ,
p.
217.
Lohse, Detlef
and
Zhang, Xuehua
2020.
Physicochemical hydrodynamics of droplets out of equilibrium.
Nature Reviews Physics,
Vol. 2,
Issue. 8,
p.
426.
Encarnación Escobar, José M.
Nieland, Jaap
van Houselt, Arie
Zhang, Xuehua
and
Lohse, Detlef
2020.
Marangoni puffs: dramatically enhanced dissolution of droplets with an entrapped bubble.
Soft Matter,
Vol. 16,
Issue. 18,
p.
4520.
Meng, Jia
You, Jae Bem
and
Zhang, Xuehua
2020.
Viscosity-Mediated Growth and Coalescence of Surface Nanodroplets.
The Journal of Physical Chemistry C,
Vol. 124,
Issue. 23,
p.
12476.
Chong, Kai Leong
Li, Yanshen
Ng, Chong Shen
Verzicco, Roberto
and
Lohse, Detlef
2020.
Convection-dominated dissolution for single and multiple immersed sessile droplets.
Journal of Fluid Mechanics,
Vol. 892,
Issue. ,
Lopez de la Cruz, Ricardo Arturo
Diddens, Christian
Zhang, Xuehua
and
Lohse, Detlef
2022.
Oscillatory droplet dissolution from competing Marangoni and gravitational flows.
Physical Review Fluids,
Vol. 7,
Issue. 9,
Zeng, Binglin
Wang, Yuliang
Diddens, Christian
Zandvliet, Harold J. W.
and
Lohse, Detlef
2022.
Droplet dissolution driven by emerging thermal gradients and Marangoni flow.
Physical Review Fluids,
Vol. 7,
Issue. 6,
Lee, You-An
Sun, Chao
Huisman, Sander G.
and
Lohse, Detlef
2022.
Micro-droplet nucleation through solvent exchange in a turbulent buoyant jet.
Journal of Fluid Mechanics,
Vol. 943,
Issue. ,
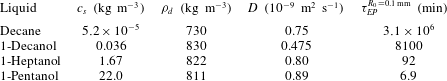
$25\,^{\circ }\text{C}$ and ambient pressure and the resulting Epstein–Plesset time scale
$\unicode[STIX]{x1D70F}_{EP}=R_{0}^{2}\unicode[STIX]{x1D70C}_{d}/(Dc_{s})$ for a
$R_{0}=0.1~\text{mm}$ droplet.





1 Introduction: the Epstein–Plesset droplet
When a droplet of liquid comes into contact with water, we tend to think only in two categories, ‘insoluble’ or ‘soluble’: e.g. an olive oil droplet is seen as insoluble, whereas an ethanol droplet is soluble and in fact perfectly miscible with water. However, the truth lies in the middle: solubility is a matter of time scales, and even heavy oil dissolves in clean water, provided one waits long enough. The dissolution dynamics of an isolated spherical droplet in a bulk liquid at rest was analytically calculated in a classical paper by Epstein & Plesset (Reference Epstein and Plesset1950), originally formulated for bubbles and later extended to droplets (Duncan & Needham Reference Duncan and Needham2006; Su & Needham Reference Su and Needham2013). The result of this exact calculation is that a droplet shrinks with a square-root behaviour in time on a time scale governed by $\unicode[STIX]{x1D70F}_{EP}=R_{0}^{2}\unicode[STIX]{x1D70C}_{d}/(Dc_{s})$
. Here,
$\unicode[STIX]{x1D70F}_{EP}=R_{0}^{2}\unicode[STIX]{x1D70C}_{d}/(Dc_{s})$
. Here,
 $c_{s}$
is the solubility of the solute in the solvent,
$c_{s}$
is the solubility of the solute in the solvent,
 $\unicode[STIX]{x1D70C}_{d}$
the droplet density,
$\unicode[STIX]{x1D70C}_{d}$
the droplet density,
 $D$
the diffusion constant and
$D$
the diffusion constant and
 $R_{0}$
the initial droplet radius. While the density and diffusivity of liquid solutes do not vary too much, their solubility in water can vary by many orders of magnitude, leading to huge lifetime differences between different drops of the same size (table 1). Here we assumed that the surrounding water far away from the droplet does not contain any solute. Once the solute concentration
$R_{0}$
the initial droplet radius. While the density and diffusivity of liquid solutes do not vary too much, their solubility in water can vary by many orders of magnitude, leading to huge lifetime differences between different drops of the same size (table 1). Here we assumed that the surrounding water far away from the droplet does not contain any solute. Once the solute concentration
 $c_{\infty }$
far away from the drop is non-zero, the dissolution is delayed (by a factor
$c_{\infty }$
far away from the drop is non-zero, the dissolution is delayed (by a factor
 $c_{s}/(c_{s}-c_{\infty })$
) and for positive oversaturation
$c_{s}/(c_{s}-c_{\infty })$
) and for positive oversaturation
 $\unicode[STIX]{x1D701}=c_{\infty }/c_{s}-1>0$
the droplet will even grow.
$\unicode[STIX]{x1D701}=c_{\infty }/c_{s}-1>0$
the droplet will even grow.
Table 1. Material properties of various liquids in water at $25\,^{\circ }\text{C}$
and ambient pressure and the resulting Epstein–Plesset time scale
$25\,^{\circ }\text{C}$
and ambient pressure and the resulting Epstein–Plesset time scale
 $\unicode[STIX]{x1D70F}_{EP}=R_{0}^{2}\unicode[STIX]{x1D70C}_{d}/(Dc_{s})$
for a
$\unicode[STIX]{x1D70F}_{EP}=R_{0}^{2}\unicode[STIX]{x1D70C}_{d}/(Dc_{s})$
for a
 $R_{0}=0.1~\text{mm}$
droplet.
$R_{0}=0.1~\text{mm}$
droplet.
The Epstein–Plesset problem can be seen as the ‘hydrogen atom’ of diffusive droplet or bubble dynamics, as it can be solved analytically. But just as an isolated hydrogen atom is rare and hard to realize and the relevant real world consists of larger atoms, molecules and solid-state matter, in real-world fluid dynamics problems we hardly ever have an isolated droplet or bubble in a bulk liquid at rest, but mutually interacting droplets and bubbles, droplets and bubbles at or close to interfaces, in turbulent flow and with surfactants, etc. Moreover, rather than a pure gas or liquid, we often have mixtures of several gases and liquids. Just as atomic, molecular, condensed matter and solid-state physics has had to deal with the ‘complications’ of the real world, this also holds for the physics of fluids, which has to deal with the above ‘complications’.
Here we will focus on the ‘complications’ arising for droplets of liquid mixtures. While the Epstein–Plesset theory can relatively straightforwardly be extended to bubbles consisting of gas mixtures, this does not hold for multicomponent droplets, not even when they are constituted of miscible liquids. Up to now various approximations have been used: Su & Needham (Reference Su and Needham2013) assumed that the instantaneous droplet–bulk interface composition of spherical droplets can be related to the droplet volumetric composition, i.e. for a two-component droplet with liquids $i=a,b$
, they assume
$i=a,b$
, they assume
 $V_{a}/V_{b}=A_{a}/A_{b}$
, where
$V_{a}/V_{b}=A_{a}/A_{b}$
, where
 $V_{i}/V$
and
$V_{i}/V$
and
 $A_{i}/A$
are the volume and area fractions of the total droplet volume
$A_{i}/A$
are the volume and area fractions of the total droplet volume
 $V$
and the total droplet interface
$V$
and the total droplet interface
 $A$
. Su & Needham (Reference Su and Needham2013) then calculated the dissolution rate of the individual components based on the total droplet radius, and multiplied this by the surface area fraction
$A$
. Su & Needham (Reference Su and Needham2013) then calculated the dissolution rate of the individual components based on the total droplet radius, and multiplied this by the surface area fraction
 $A_{i}/A$
occupied by the respective component. This approach is equivalent to the use of Raoult’s law to determine the partial gas pressures at the bulk side of the interface, in the sense that both approaches assume negligible interaction between the two components
$A_{i}/A$
occupied by the respective component. This approach is equivalent to the use of Raoult’s law to determine the partial gas pressures at the bulk side of the interface, in the sense that both approaches assume negligible interaction between the two components
 $a$
and
$a$
and
 $b$
, and a homogeneous mixture inside the droplet.
$b$
, and a homogeneous mixture inside the droplet.
2 Beyond Epstein–Plesset
In a recent paper, Chu & Prosperetti (Reference Chu and Prosperetti2016) have now provided a calculation of the dissolution (or growth) problem of a multicomponent droplet, revealing the limitation of the hitherto used approximations. They solve the diffusion equation with concentration boundary conditions at the (moving) droplet interface following from the requirement that the chemical potentials of each of the components have the same value in both phases (Landau & Lifshitz Reference Landau and Lifshitz1986), assuming thermodynamic equilibrium. Remarkably, these concentration boundary conditions lead to time-dependent concentrations at the droplet interface, resulting in a memory term for the mass flux through the interface, which does not exist for a droplet of a pure liquid. How serious are the deviations from the hitherto used approximations depends strongly on the solubilities and diffusivities of the components. For similar solubilities and diffusivities of the two droplet components, they can be serious, and Chu & Prosperetti (Reference Chu and Prosperetti2016) construct a case in which the two-component droplet grows, even though in the solution both constituents of the droplet have a concentration below their saturation concentration, i.e. $\unicode[STIX]{x1D701}_{i}<0$
for both
$\unicode[STIX]{x1D701}_{i}<0$
for both
 $i=a,b$
.
$i=a,b$
.
Chu & Prosperetti (Reference Chu and Prosperetti2016) performed their calculation for an immersed two-component spherical droplet in a still solvent, but they also sketched how to embody further ‘complications’ of the real world, namely to an immersed sessile droplet (to which an Epstein–Plesset type approach for the dissolution or growth can also be extended (Lohse & Zhang Reference Lohse and Zhang2015)) consisting of two components, to two-component droplets in a flow situation, and to droplets consisting of more than two components.
The pioneering calculations by Chu & Prosperetti (Reference Chu and Prosperetti2016) stimulated us to perform detailed experiments on dissolving sessile two-component droplets (Dietrich et al. Reference Dietrich, Rump, Lv, Kooij, Zandvliet and Lohse2016). As predicted by Chu & Prosperetti (Reference Chu and Prosperetti2016), we indeed find cases in which a segregation of the (miscible!) droplet components at the droplet interface can take place. Two snapshots of such an example are shown as confocal images of a dissolving pentanol/cyclohexane droplet in the figure by the title of this paper. Note that, for sessile droplets, due to the broken spherical symmetry, spatially inhomogeneous dissolution (or evaporation in air) may take place, also leading to segregation of the component in addition to Marangoni flow (Cazabat & Guéna Reference Cazabat and Guéna2010). Obviously, many more experiments should be done to quantitatively study the dissolution and growth of multicomponent droplets and to compare with the theory of Chu & Prosperetti (Reference Chu and Prosperetti2016).
3 Relevance
The results of Chu & Prosperetti (Reference Chu and Prosperetti2016) have tremendous relevance for various applications in chemical technology and analysis. Here I would like to highlight the process of liquid–liquid extraction. For chemical analysis such as chromatography, ever since the pioneering work of the Nobel Laureate Pregl (Reference Pregl1917) on microanalysis, there have been continuous efforts to further miniaturize the extraction process of the analyte and to optimize the extraction recovery and preconcentration factor. In the last two decades so-called single-drop microextraction (see e.g. the review of Jain & Verma (Reference Jain and Verma2011)) have become very popular for sample preparation of trace organic and inorganic analysis. The principle of this method is shown in figure 1. Here a solute A dissolved in water accumulates in the droplet of water-immiscible liquid B, due its higher solubility in B as compared to in water. After an equilibrium has been achieved, the droplet, which now consists of a mixture of A and B, is extracted with a syringe, in order to be further analysed by, for example, chromatography. Hitherto it has not been possible to calculate a priori the extraction recovery and the preconcentration factor. The work by Chu & Prosperetti (Reference Chu and Prosperetti2016) now offers opportunities to do so in the future in order to further optimize the microextraction process. Obviously, one then has to go beyond the case of still liquid and include the effect of turbulent mixing of the flow, which will accelerate the transfer of the analyte to the droplet.
Figure 1. Principle of single-drop microextraction: a solute A dissolved in water has higher solubility in the liquid B of the immersed droplet, which has very poor miscibility with water. Once A has accumulated in the drop B, it is extracted with the syringe.
The scale on which single-drop microextraction can be done remains limited, but this limitation is overcome in the modern technique of dispersive liquid–liquid microextraction, invented by Rezaee et al. (Reference Rezaee, Assadi, Hosseinia, Aghaee, Ahmadi and Berijani2006) and Rezaee, Yamini & Faraji (Reference Rezaee, Yamini and Faraji2010). Here, a mixture of two miscible liquids B and C (with low concentration of B) is put into water with the analyte A, with B being immiscible with water, but C being miscible. When poured into water, droplets of B will immediately nucleate. The liquid B is chosen such that the analyte A easily dissolved in it and it is heavier than water and liquid C. The final step is to centrifuge the dispersion and take out the A–B phase. Again, the work by Chu & Prosperetti (Reference Chu and Prosperetti2016) offers an approach towards a quantitative understanding of the fluid dynamics of such liquid–liquid microextraction processes, in the spirit of the famous book by Levich (Reference Levich1962).
Acknowledgements
The author is very grateful to A. Prosperetti and X. Zhang for various illuminating discussions. We thank E. Dietrich, P. Ly and coauthors for providing the figure by the title.