Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-25T04:55:21.409Z Has data issue: false hasContentIssue false
  • English
  • Français

Towards a finite-time singularity of the Navier–Stokes equations Part 1. Derivation and analysis of dynamical system

Published online by Cambridge University Press:  31 December 2018

H. K. Moffatt Open the ORCID record for H. K. Moffatt [Opens in a new window]  and
Yoshifumi Kimura
H. K. Moffatt*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
Yoshifumi Kimura
Affiliation:
Graduate School of Mathematics, Nagoya University, Furo-cho, Chikusa-ku, Nagoya 464-8602, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The evolution towards a finite-time singularity of the Navier–Stokes equations for flow of an incompressible fluid of kinematic viscosity $\unicode[STIX]{x1D708}$ is studied, starting from a finite-energy configuration of two vortex rings of circulation 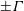$\pm \unicode[STIX]{x1D6E4}$ and radius 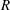$R$, symmetrically placed on two planes at angles 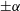$\pm \unicode[STIX]{x1D6FC}$ to a plane of symmetry $x=0$. The minimum separation of the vortices, 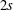$2s$, and the scale of the core cross-section, 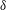$\unicode[STIX]{x1D6FF}$, are supposed to satisfy the initial inequalities 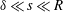$\unicode[STIX]{x1D6FF}\ll s\ll R$, and the vortex Reynolds number 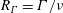$R_{\unicode[STIX]{x1D6E4}}=\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D708}$ is supposed very large. It is argued that in the subsequent evolution, the behaviour near the points of closest approach of the vortices (the ‘tipping points’) is determined solely by the curvature 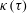$\unicode[STIX]{x1D705}(\unicode[STIX]{x1D70F})$ at the tipping points and by 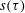$s(\unicode[STIX]{x1D70F})$ and 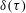$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70F})$, where 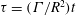$\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D6E4}/R^{2})t$ is a dimensionless time variable. The Biot–Savart law is used to obtain analytical expressions for the rate of change of these three variables, and a nonlinear dynamical system relating them is thereby obtained. The solution shows a finite-time singularity, but the Biot–Savart law breaks down just before this singularity is realised, when 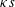$\unicode[STIX]{x1D705}s$ and 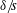$\unicode[STIX]{x1D6FF}/\!s$ become of order unity. The dynamical system admits ‘partial Leray scaling’ of just $s$ and $\unicode[STIX]{x1D705}$, and ultimately full Leray scaling of 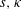$s,\unicode[STIX]{x1D705}$ and $\unicode[STIX]{x1D6FF}$, conditions for which are obtained. The tipping point trajectories are determined; these meet at the singularity point at a finite angle. An alternative model is briefly considered, in which the initial vortices are ovoidal in shape, approximately hyperbolic near the tipping points, for which there is no restriction on the initial value of the parameter $\unicode[STIX]{x1D705}$; however, it is still the circles of curvature at the tipping points that determine the local evolution, so the same dynamical system is obtained, with breakdown again of the Biot–Savart approach just before the incipient singularity is realised. The Euler flow situation (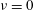$\unicode[STIX]{x1D708}=0$) is considered, and it is conjectured on the basis of the above dynamical system that a finite-time singularity can indeed occur in this case.

JFM classification

Vortex Flows: Vortex dynamics Vortex Flows: Vortex Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 861 , 25 February 2019 , pp. 930 - 967
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, A. I.(Eds) 1964 Handbook of Mathematical Functions, Dover.Google Scholar
Beale, J. T., Kato, T. & Majda, A. 1984 Remarks on the breakdown of smooth solutions for the 3D Euler equations. Commun. Math. Phys. 94, 61–66.Google Scholar
Bewley, G. P., Paoletti, M. S., Sreenivasan, K. R. & Lathrop, D. P. 2008 Characterization of reconnecting vortices in superfluid helium. Proc. Natl Acad. Sci. USA 105, 13707–13710.Google Scholar
Boué, L., Khomenko, D., L’vov, V. S. & Procaccia, I. 2013 Analytic solution of the approach of quantum vortices towards reconnection. Phys. Rev. Lett. 111, 145302.Google Scholar
Brenner, M. P., Hormoz, S. & Pumir, A. 2016 Potential singularity mechanism for the Euler equations. Phys. Rev. Fluids 1, 084503.Google Scholar
Bustamante, M. D. & Kerr, R. M. 2008 3D Euler about a 2D symmetry plane. Physica D 237 (14), 1912–1920.Google Scholar
Caffarelli, L., Kohn, R. & Nirenberg, L. 1982 Partial regularity of suitable weak solutions of the Navier–Stokes equations. Commun. Pure Appl. Maths 35, 771–831.Google Scholar
Constantin, P., Fefferman, C. & Majda, A. J. 1996 Geometric constraints on potentially singular solutions for the 3-D Euler equations. Commun. Part. Diff. Equ. 21 (3–4), 441146.Google Scholar
Deng, J., Hou, T. Y. & Yu, X. 2005 Geometric properties and nonblowup of 3D incompressible Euler flow. Commun. Part. Diff. Equ. 30 (1–2), 225–243.Google Scholar
Doering, C. R. 2009 The 3D Navier–Stokes problem. Annu. Rev. Fluid Mech. 41, 109–128.Google Scholar
Eggers, J. & Fontelos, M. A. 2015 Singularities: Formation, Structure, and Propagation. Cambridge University Press.Google Scholar
Escauriaza, L., Seregin, G. A. & Šverák, V. 2003 L 3, ∞ -solutions of the Navier–Stokes equations and backward uniqueness. Russian Math. Surveys 58, 211–261.Google Scholar
Fefferman, C. L. 2006 The Millennium Prize Problems, pp. 57–70. American Mathematical Society.Google Scholar
Foias, C., Hoang, L. & Saut, J.-C. 2018 Navier and Stokes meet Poincaré and Dulac. J. Appl. Anal. Comp. 8 (3), 727–763.Google Scholar
Foias, C. & Temam, R. 1989 Gevrey class regularity for the solutions of the Navier–Stokes equations. J. Funct. Anal. 87 (2), 359–369.Google Scholar
Habibah, U., Nakagawa, H. & Fukumoto, Y. 2018 Finite-thickness effect on speed of a counter-rotating vortex pair at high Reynolds numbers. Fluid Dyn. Res. 50, 031401.Google Scholar
Hormoz, S. & Brenner, M. P. 2012 Absence of singular stretching of interacting vortex filaments. J. Fluid Mech. 707, 191–204.Google Scholar
Hou, T. & Li, R. 2006 Dynamic depletion of vortex stretching and non-blowup of the 3-D incompressible Euler equations. J. Nonlinear Sci. 16, 639–664.Google Scholar
Hou, T. Y. & Li, R. 2008 Blowup or no blowup? The interplay between theory and numerics. Physica D 237 (14), 1937–1944.Google Scholar
Kerr, R. M. 2005a Velocity and scaling of collapsing Euler vortices. Phys. Fluids 17, 075103.Google Scholar
Kerr, R. M. 2005b Vortex collapse and turbulence. Fluid Dyn. Res. 36 (4), 249–260.Google Scholar
Kerr, R. M. & Hussain, F. 1989 Simulation of vortex reconnection. Physica D 37 (1), 474–484.Google Scholar
Kida, S., Takaoka, M. & Hussain, F. 1991 Collision of two vortex rings. J. Fluid Mech. 230, 583–646.Google Scholar
Kimura, Y. & Moffatt, H. K. 2018a Scaling properties towards vortex reconnection under the Biot–Savart law. Fluid Dyn. Res. 50, 011409.Google Scholar
Kimura, Y. & Moffatt, H. K. 2018b A tent model of vortex reconnection under Biot–Savart evolution. J. Fluid Mech. 834, R1.Google Scholar
Kleckner, D. & Irvine, W. T. M. 2013 Creation and dynamics of knotted vortices. Nat. Phys. 9 (4), 253–258.Google Scholar
Lemarié-Rieusset, P. G. 2016 The Navier–Stokes Problem in the XXIst Century. CRC Press, Taylor & Francis Group, Chapman & Hall.Google Scholar
Leray, J. 1934 Sur un liquide visqueux emplissant l’espace. Acta Math. 63, 193–248.Google Scholar
Lin, S. J. & Corcos, G. M. 1984 The mixing layer: deterministic models of a turbulent flow. Part 3. The effect of plane strain on the dynamics of streamwise vortices. J. Fluid Mech. 141, 139–178.Google Scholar
McKeown, R., Ostilla-Monico, R., Pumir, A., Brenner, M. P. & Rubinstein, S. M.2018 A cascade leading to the emergence of small structures in vortex ring collisions. Preprint, arXiv:1802.09973v2 [physics.flu-dyn].Google Scholar
Moffatt, H. K. 1969 The degree of knottedness of tangled vortex lines. J. Fluid Mech. 35, 117–129.Google Scholar
Moffatt, H. K. 2000 The interaction of skewed vortex pairs: a model for blow-up of the Navier–Stokes equations. J. Fluid Mech. 409, 51–68.Google Scholar
Moffatt, H. K., Kida, S. & Ohkitani, K. 1994 Stretched vortices – the sinews of turbulence; large-Reynolds-number asymptotics. J. Fluid Mech. 259, 241–264.Google Scholar
Moffatt, H. K. & Ricca, R. L. 1992 Helicity and the Călugăreanu invariant. Proc. R. Soc. Lond. A 439, 411–429.Google Scholar
Neu, J. 1984 The dynamics of stretched vortices. J. Fluid Mech. 143, 253–276.Google Scholar
Pierrehumbert, R. T. 1980 A family of steady, translating vortex pairs with distributed vorticity. J. Fluid Mech. 99, 129–144.Google Scholar
Pumir, A. & Siggia, E. D. 1987 Vortex dynamics and the existence of solutions to the Navier–Stokes equations. Phys. Fluids 30, 1606–1626.Google Scholar
Robinson, A. C. & Saffman, P. G. 1984 Stability and structure of stretched vortices. Stud. Appl. Maths 70 (2), 163–181.Google Scholar
Saffman, P. G. 1970 The velocity of viscous vortex rings. Stud. Appl. Maths 49, 371–380.Google Scholar
Saffman, P. G. & Tanveer, S. 1982 The touching pair of equal and opposite uniform vortices. Phys. Fluids 25, 1929–1930.Google Scholar
Scheeler, M. W., van Rees, W. M., Kedia, H., Kleckner, D. & Irvine, W. T. M. 2017 Complete measurement of helicity and its dynamics in vortex tubes. Science 357, 487–491.Google Scholar
Schwarz, K. W. 1985 Three-dimensional vortex dynamics in superfluid He4: line–line and line–boundary interactions. Phys. Rev. B 31 (9), 5782.Google Scholar
Seregin, G. & Šverák, V. 2002 Navier–Stokes equations with lower bounds on the pressure. Arch. Rat. Mech. Anal. 163, 65–86.Google Scholar
Siggia, E. D. 1985 Collapse and amplification of a vortex filament. Phys. Fluids 28, 794–805.Google Scholar
Siggia, E. D. & Pumir, A. 1985 Incipient singularities in the Navier–Stokes equations. Phys. Rev. Lett. 55, 1749–1752.Google Scholar
Sullivan, I. S., Niemela, J. J., Hershberger, R. E., Bolster, D. & Donnelly, R. J. 2008 Dynamics of thin vortex rings. J. Fluid Mech. 609, 319–347.Google Scholar
de Waele, A. T. A. M. & Aarts, R. G. K. M. 1994 Route to vortex reconnection. Phys. Rev. Lett. 72 (4), 482–485.Google Scholar

Moffatt and Kimura supplementary movie 1

Biot-Savart approach to a singularity, as described in the caption to figure 1.

Download Moffatt and Kimura supplementary movie 1(Video)
Video 10 MB