Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-29T05:19:06.737Z Has data issue: false hasContentIssue false
  • English
  • Français

Torque scaling at primary and secondary bifurcations in a Taylor–Couette flow of suspensions

Published online by Cambridge University Press:  22 February 2022

Masoud Moazzen Open the ORCID record for Masoud Moazzen [Opens in a new window] ,
Tom Lacassagne Open the ORCID record for Tom Lacassagne [Opens in a new window] ,
Vincent Thomy  and
S. Amir Bahrani Open the ORCID record for S. Amir Bahrani [Opens in a new window]
Masoud Moazzen
Affiliation:
IMT Nord Europe, Institut Mines Télécom, Univ. Lille, Center for Energy and Environment, F-59000Lille, France
Tom Lacassagne
Affiliation:
IMT Nord Europe, Institut Mines Télécom, Univ. Lille, Center for Energy and Environment, F-59000Lille, France
Vincent Thomy
Affiliation:
Univ. Lille, CNRS, Centrale Lille, Univ. Polytechnique Hauts-de-France, UMR 8520 - IEMN – Institut d'Electronique de Microélectronique et de Nanotechnologie, F-59000Lille, France
S. Amir Bahrani*
Affiliation:
IMT Nord Europe, Institut Mines Télécom, Univ. Lille, Center for Energy and Environment, F-59000Lille, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

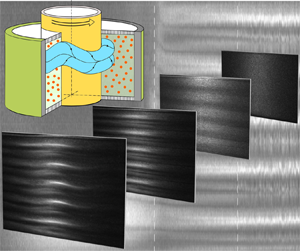
The Taylor–Couette flow of non-colloidal, neutrally buoyant spherical particle suspensions in the $\phi =0\,\%-28\,\%$ concentration range and (17–250) Reynolds number ($\mathcal {R})$ range is studied using synchronized flow visualization and torque measurements. Both methods are applied in ramp-up/down (acceleration/deceleration of the inner cylinder) experiments to detect the various flow structure states and bifurcation natures, their critical conditions and their lifetime in $\mathcal {R}$ range. Torque measurement allows us to discuss the evolution of the (pseudo) Nusselt number, $\mathcal {N}$, and friction coefficient with $\mathcal {R}$ or alternatively the Taylor number, Ta. Flow visualization brings additional information on the unsteady dynamics of flow states. For concentrations higher than $\phi =6\,\%$, two unsteady (spiral vortex flow, wavy vortex flow) and one steady (Taylor vortex flow) flow state are observed in both ramp-up/down experiments. Hysteretic behaviour is reported for some primary, secondary and tertiary bifurcations, which are thus found to be subcritical. A critical concentration is observed at $\phi =15\,\%$ for the range of $\mathcal {R}$ at which spiral vortex flow is encountered. Characteristic frequencies of unsteady flow state (spiral vortex flow, wavy vortex flow) for different suspension concentrations are evaluated. Finally, three hydrodynamic concentration subregimes are identified for the first time, with their distinct sets of concentration-dependent critical conditions, torque scaling exponents and friction coefficients.

JFM classification

Complex Fluids: Suspensions Instability: Instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 937 , 25 April 2022 , A2
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abcha, N., Latrache, N., Dumouchel, F. & Mutabazi, I. 2008 Qualitative relation between reflected light intensity by Kalliroscope flakes and velocity field in the Couette–Taylor flow system. Exp. Fluids 45 (1), 85–94.CrossRefGoogle Scholar
Akbarzadeh, K., Eskin, D., Ratulowski, J. & Taylor, S. 2012 Asphaltene deposition measurement and modeling for flow assurance of tubings and flow lines. In Energy and Fuels, vol. 26, pp. 495–510. American Chemical Society.CrossRefGoogle Scholar
Ali, M.E., Mitra, D., Schwille, J.A. & Lueptow, R.M. 2002 Hydrodynamic stability of a suspension in cylindrical Couette flow. Phys. Fluids 14 (3), 1236–1243.CrossRefGoogle Scholar
Alibenyahia, B., Lemaitre, C., Nouar, C. & Ait-Messaoudene, N. 2012 Revisiting the stability of circular Couette flow of shear-thinning fluids. J. Non-Newtonian Fluid Mech. 183–184, 37–51.CrossRefGoogle Scholar
Ancey, C. & Vollm, P. 2005 Rhéophysique des suspensions concentrées : cadre théorique et similitude. 17 ‘eme Congr‘es Français de Mécanique, 1–12.Google Scholar
Annesini, M.C., Marrelli, L., Piemonte, V. & Turchetti, L. 2017 Blood oxygenators and artificial lungs. In Artificial Organ Engineering, pp. 117–161. Springer.CrossRefGoogle Scholar
Bahrani, S.A. & Nouar, C. 2014 Intermittency in the transition to turbulence for a shear-thinning fluid in Hagen–Poiseuille flow. J. Appl. Fluid Mech. 7 (1), 1–6.Google Scholar
Baroudi, L., Majji, M.V. & Morris, J.F. 2020 Effect of inertial migration of particles on flow transitions of a suspension Taylor–Couette flow. Phys. Rev. Fluids 5 (11), 114303.CrossRefGoogle Scholar
Benjamin, T.B. 1978 Bifurcation phenomena in steady flows of a viscous fluid. Part I: theory. Proc. R. Soc. Lond. A 359 (1696), 1–26. The Royal Society London.Google Scholar
Blanc, F., Peters, F. & Lemaire, E. 2011 Experimental signature of the pair trajectories of rough spheres in the shear-induced microstructure in noncolloidal suspensions. Phys. Rev. Lett. 107 (20), 208302.CrossRefGoogle ScholarPubMed
Bödewadt, U.T. 1940 Die Drehströmung über festem Grunde. Z. Angew. Math. Mech. 20 (5), 241–253.CrossRefGoogle Scholar
Borrero-Echeverry, D., Crowley, C.J. & Riddick, T.P. 2018 Rheoscopic fluids in a post-Kalliroscope world. Phys. Fluids 30 (8), 087103.CrossRefGoogle Scholar
Burkhalter, J.E. & Koschmieder, E.L. 1973 Steady supercritical Taylor vortex flow. J. Fluid Mech. 58 (3), 547–560.CrossRefGoogle Scholar
Cagney, N. & Balabani, S. 2019 Taylor–Couette flow of shear-thinning fluids. Phys. Fluids 31 (5), 53102.CrossRefGoogle Scholar
Cliffe, K.A., Mullin, T. & Schaeffer, D. 2012 The onset of steady vortices in Taylor–Couette flow: the role of approximate symmetry. Phys. Fluids 24, 64102.CrossRefGoogle Scholar
Cole, J.A. 1976 Taylor-vortex instability and annulus-length effects. J. Fluid Mech. 75 (1), 1–15.CrossRefGoogle Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21 (3), 385–425.CrossRefGoogle Scholar
Couette, M 1890 Études sur le frottement des liquides. Ann. Chim. Phys. 21 (21), 433–510.Google Scholar
Czarny, O.A. 2003 Contribution to numerical study of rotating flows with walls. An application to the Taylor–Couette system. PhD thesis, Université de la Méditerranée – Aix-Marseille II.Google Scholar
Da Cunha, F.R. & Hinch, E.J. 1996 Shear-induced dispersion in a dilute suspension of rough spheres. J. Fluid Mech. 309, 211–223.CrossRefGoogle Scholar
Dash, A., Anantharaman, A., Greidanus, A. & Poelma, C. 2019 Simultaneous ultrasound imaging velocimetry (UIV) and flow visualization in Taylor–Couette flows: validation of UIV in single-phase flows. In Proceedings of the 13th International Symposium on Particle Image Velocimetry (ISPIV 2019), pp. 980–989. Universitat der Bundeswehr Munchen.Google Scholar
Dash, A., Anantharaman, A. & Poelma, C. 2020 Particle-laden Taylor–Couette flows: higher-order transitions and evidence for azimuthally localized wavy vortices. J. Fluid Mech. 903, A20.CrossRefGoogle Scholar
DiPrima, R.C., Eagles, P.M. & Ng, B.S. 1984 The effect of radius ratio on the stability of Couette flow and Taylor vortex flow. Phys. Fluids 27 (10), 2403–2411.CrossRefGoogle Scholar
Drazer, G., Koplik, J., Khusid, B. & Acrivos, A. 2002 Deterministic and stochastic behaviour of non-Brownian spheres in sheared suspensions. J. Fluid Mech. 460, 307–335.CrossRefGoogle Scholar
Dutcher, C.S. & Muller, S.J. 2009 Spatio-temporal mode dynamics and higher order transitions in high aspect ratio Newtonian Taylor–Couette flows. J. Fluid Mech. 641, 85–113.CrossRefGoogle Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2000 Scaling of global momentum transport in Taylor–Couette and pipe flow. Eur. Phys. J. B 18 (3), 541–544.CrossRefGoogle Scholar
Ekman, V.W. 1905 On the influence of the Earth's rotation on ocean-currents. Ark. Mat. Astr. Fys. 2 (11), 1–52.Google Scholar
Gebhardt, T. & Grossmann, S. 1993 The Taylor–Couette eigenvalue problem with independently rotating cylinders. Z. für Physik B Condens. Matter 90 (4), 475–490.CrossRefGoogle Scholar
Gillissen, J.J.J., Cagney, N., Lacassagne, T., Papadopoulou, A., Balabani, S. & Wilson, H.J. 2020 Taylor–Couette instability in disk suspensions: experimental observation and theory. Phys. Rev. Fluids 5 (8), 083302.CrossRefGoogle Scholar
Gillissen, J.J.J. & Wilson, H.J. 2019 Taylor–Couette instability in sphere suspensions. Phys. Rev. Fluids 4 (4), 043301.CrossRefGoogle Scholar
Giordano, R.L.C., Giordano, R.C. & Cooney, C.L. 2000 Performance of a continuous Taylor–Couette–Poiseuille vortex flow enzymic reactor with suspended particles. Process Biochem. 35 (10), 1093–1101.CrossRefGoogle Scholar
Grossmann, S., Lohse, D. & Sun, C. 2016 High-Reynolds number Taylor–Couette turbulence. Annu. Rev. Fluid Mech. 48 (1), 53–80.CrossRefGoogle Scholar
Guazzelli, É. & Pouliquen, O. 2018 Rheology of dense granular suspensions. J. Fluid Mech. 852, P11–P173.CrossRefGoogle Scholar
Halow, J.S. & Wills, G.B. 1970 Radial migration of spherical particles in Couette systems. AIChE J. 16 (2), 281–286.CrossRefGoogle Scholar
Han, M., Kim, C., Kim, M. & Lee, S. 1999 Particle migration in tube flow of suspensions. J. Rheol. 43 (5), 1157–1174.CrossRefGoogle Scholar
Heirman, G., Hendrickx, R., Vandewalle, L., Van Gemert, D., Feys, D., De Schutter, G., Desmet, B. & Vantomme, J. 2009 Integration approach of the Couette inverse problem of powder type self-compacting concrete in a wide-gap concentric cylinder rheometer. Part II. Influence of mineral additions and chemical admixtures on the shear thickening flow behaviour. Cement Concrete Res. 39 (3), 171–181.CrossRefGoogle Scholar
Hildebrandt, J.R. & Saxton, J.B. 1987 Use of Taylor vortices in protein processing to enhance membrane filtration performance. Bioprocess Engng Colloquium, pp. 93–96.Google Scholar
Kang, C. & Mirbod, P. 2021 Flow instability and transitions in Taylor–Couette flow of a semidilute non-colloidal suspension. J. Fluid Mech. 916, A12.CrossRefGoogle Scholar
Koh, C.J., Hookham, P. & Leal, L.G. 1994 An experimental investigation of concentrated suspension flows in a rectangular channel. J. Fluid Mech. 266 (115), 1–32.CrossRefGoogle Scholar
Krieger, I.M. & Dougherty, T.J. 1959 A mechanism for non-Newtonian flow in suspensions of rigid spheres. Trans. Soc. Rheol. 3 (1), 137–152.CrossRefGoogle Scholar
Lacassagne, T., Cagney, N. & Balabani, S. 2021 Shear-thinning mediation of elasto-inertial Taylor–Couette flow. J. Fluid Mech. 915, A91.CrossRefGoogle Scholar
Loisel, V., Abbas, M., Masbernat, O. & Climent, E. 2013 The effect of neutrally buoyant finite-size particles on channel flows in the laminar-turbulent transition regime. Phys. Fluids 25 (12), 123304.CrossRefGoogle Scholar
Lomholt, S. & Maxey, M.R. 2003 Force-coupling method for particulate two-phase flow: Stokes flow. J. Comput. Phys. 184 (2), 381–405.CrossRefGoogle Scholar
Majji, M.V., Banerjee, S. & Morris, J.F. 2018 Inertial flow transitions of a suspension in Taylor–Couette geometry. J. Fluid Mech. 835, 936–969.CrossRefGoogle Scholar
Majji, M.V. & Morris, J.F. 2018 Inertial migration of particles in Taylor–Couette flows. Phys. Fluids 30 (3), 033303.CrossRefGoogle Scholar
Mallock, A. 1896 III. Experiments on fluid viscosity. Phil. Trans. R. Soc. Lond. A 187, 41–56.Google Scholar
Matas, J.P., Morris, J.F. & Guazzelli, É. 2003 Transition to turbulence in particulate pipe flow. Phys. Rev. Lett. 90 (1), 4.CrossRefGoogle ScholarPubMed
Matas, J.P., Morris, J.F. & Guazzelli, É. 2009 Lateral force on a rigid sphere in large-inertia laminar pipe flow. J. Fluid Mech. 621, 59–67.CrossRefGoogle Scholar
Morris, J.F. 2009 A review of microstructure in concentrated suspensions and its implications for rheology and bulk flow. Rheol. Acta 48 (8), 909–923.CrossRefGoogle Scholar
Morris, J.F. & Boulay, F. 1999 Curvilinear flows of noncolloidal suspensions: the role of normal stresses. J. Rheol. 43 (5), 1213–1237.CrossRefGoogle Scholar
Mullin, T., Heise, M. & Pfister, G. 2017 Onset of cellular motion in Taylor–Couette flow. Phys. Rev. Fluids 2 (8), 081901.CrossRefGoogle Scholar
Nemri, M. 2013 Étude expérimentale et numérique du mélange et de la dispersion axiale dans une colonne à effet Taylor–Couette. PhD thesis. Institut National Polytechnique de Toulouse.Google Scholar
Peixinho, J. 2015 Fluid dynamics, instabilities, turbulence and complex fluids. Habilitation à diriger des recherches, Université du Havre.Google Scholar
Pfister, G. & Gerdts, U. 1981 Dynamics of Taylor wavy vortex flow. Phys. Lett. A 83 (1), 23–25.CrossRefGoogle Scholar
Ramesh, P. & Alam, M. 2020 Interpenetrating spiral vortices and other coexisting states in suspension Taylor–Couette flow. Phys. Rev. Fluids 5 (4), 042301.CrossRefGoogle Scholar
Ramesh, P., Bharadwaj, S. & Alam, M. 2019 Suspension Taylor–Couette flow: co-existence of stationary and travelling waves, and the characteristics of Taylor vortices and spirals. J. Fluid Mech. 870, 901–940.CrossRefGoogle Scholar
Rashedi, A., Ovarlez, G. & Hormozi, S. 2020 Engineered transparent emulsion to optically study particulate flows in yield stress fluids. Exp. Fluids 61 (2), 22.CrossRefGoogle Scholar
Rayleigh, Lord 1917 On the dynamics of revolving fluids. Proc. R. Soc. Lond. A 93 (648), 148–154.Google Scholar
Rebouças, R.B., Siqueira, I.R., de Souza Mendes, P.R. & Carvalho, M.S. 2016 On the pressure-driven flow of suspensions: particle migration in shear sensitive liquids. J. Non-Newtonian Fluid Mech. 234, 178–187.CrossRefGoogle Scholar
Savage, S.B. & McKeown, S. 1983 Shear stresses developed during rapid shear of concentrated suspensions of large spherical particles between concentric cylinders. J. Fluid Mech. 127, 453–472.CrossRefGoogle Scholar
Schlinker, A.C. 2017 Automated, spinning membrane filtration for preparation of mobilized leukapheresis products for CD34+ cell selection. Cell Gene Therapy Insights 3 (8), 623–637.CrossRefGoogle Scholar
Sczechowski, J.G., Koval, C.A. & Noble, R.D. 1995 A Taylor vortex reactor for heterogeneous photocatalysis. Chem. Engng Sci. 50 (20), 3163–3173.CrossRefGoogle Scholar
Stickel, J.J. & Powell, R.L. 2005 Fluid mechanics and rheology of dense suspensions. Ann. Rev. Fluid Mech. 37 (1), 129–149.CrossRefGoogle Scholar
Strogatz, S.H. 2018 Nonlinear Dynamics and Chaos. CRC.CrossRefGoogle Scholar
Taylor, G.I. 1923 VIII. Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. A 223 (605–615), 289–343.Google Scholar
Topayev, S., Nouar, C., Bernardin, D., Neveu, A. & Bahrani, S.A. 2019 Taylor-vortex flow in shear-thinning fluids. Phys. Rev. E 100 (2), 023117.CrossRefGoogle ScholarPubMed
Wali, K.C. 2001 Hydrodynamic and Hydromagnetic Stability. Dover.CrossRefGoogle Scholar