Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-24T01:39:43.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional vorticity, momentum and heat transport in a turbulent cylinder wake

Published online by Cambridge University Press:  09 November 2016

J. G. Chen ,
Y. Zhou ,
T. M. Zhou  and
R. A. Antonia
J. G. Chen
Affiliation:
Institute for Turbulence-Noise-Vibration Interactions and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055, China
Y. Zhou*
Affiliation:
Institute for Turbulence-Noise-Vibration Interactions and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055, China
T. M. Zhou
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
R. A. Antonia
Affiliation:
School of Engineering, University of Newcastle, NSW 2308, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The transport of momentum and heat in the turbulent intermediate wake of a circular cylinder is inherently three-dimensional (3-D). This work aims to gain new insight into the 3-D vorticity structure, momentum and heat transport in this flow. All three components of the velocity and vorticity vectors, along with the fluctuating temperature, are measured simultaneously, at nominally the same point in the flow, with a probe consisting of four X-wires and four cold wires. Measurements are made in the ($x$, 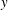$y$) or mean shear plane at 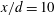$x/d=10$, 20 and 40 at a Reynolds number of 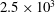$2.5\times 10^{3}$ based on the cylinder diameter $d$ and the free-stream velocity. A phase-averaging technique is developed to separate the large-scale coherent structures from the remainder of the flow. It is found that the effects of vorticity on heat transport at 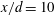$x/d=10$ and 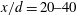$x/d=20{-}40$ are distinctly different. At 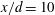$x/d=10$, both spanwise and streamwise vorticity components account significantly for the heat flux. At 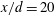$x/d=20$ and 40, the spanwise vortex rollers play a major role in inducing the coherent components of the heat flux vector, while the ribs are responsible for the small-scale heat diffusion out of the spanwise vortex rollers. The present data indicate that, if the spanwise-velocity-related terms are ignored, the estimated values of the production can have errors of approximately 22 % and 13 % respectively for the turbulent energy and temperature variance at 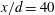$x/d=40$, and the errors are expected to further increase downstream. A conceptual model summarizing the 3-D features of the heat and momentum transports at 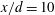$x/d=10$ is proposed. Compared with the previous two-dimensional model of Matsumura & Antonia (J. Fluid Mech., vol. 250, 1993, pp. 651–668) or MA, the new model provides a more detailed description of the role the rib-like structures undertake in transporting heat and momentum, and also underlines the importance of the upstream half of the spanwise vortex rollers, instead of only one quadrant of these rollers, as in the MA model, in diffusing heat out of the vortex.

JFM classification

Turbulent Flows: Turbulent convection Vortex Flows: Vortex Flows Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 809 , 25 December 2016 , pp. 135 - 167
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A., Browne, L. W. B., Bisset, D. K. & Fulachier, L. 1987 A description of the organized motion in the turbulent far wake of a cylinder at low Reynolds number. J. Fluid Mech. 184, 423–444.CrossRefGoogle Scholar
Antonia, R. A. & Mi, J. 1993 Temperature dissipation in a turbulent round jet. J. Fluid Mech. 250, 531–551.CrossRefGoogle Scholar
Antonia, R. A. & Mi, J. 1998 Approach towards self-preservation of turbulent cylinder and screen wakes. Exp. Therm. Fluid Sci. 17, 277–284.CrossRefGoogle Scholar
Antonia, R. A., Rajagopalan, S. & Zhu, Y. 1996 Scaling of mean square vorticity in turbulent flows. Exp. Fluids 20, 393–394.CrossRefGoogle Scholar
Antonia, R. A. & Smalley, R. J. 2000 Velocity and temperature scaling in a rough wall boundary layer. Phys. Rev. E 62, 640–646.Google Scholar
Bays-muchmore, B. & Ahmed, A. 1993 On streamwise vortices in turbulent wakes of cylinders. Phys. Fluids A 5, 387–392.CrossRefGoogle Scholar
Boirlaud, M., Couton, D. & Plourde, F. 2012 Direct numerical simulation of the turbulent wake behind a heated cylinder. Intl J. Heat Fluid Flow 38, 82–93.CrossRefGoogle Scholar
Brede, M., Eckelmann, H. & Rockwell, D. 1996 On secondary vortices in the cylinder wake. Phys. Fluids 8, 2117–2124.CrossRefGoogle Scholar
Cantwell, B. & Coles, D. 1983 An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J. Fluid Mech. 136, 321–374.CrossRefGoogle Scholar
Djenidi, L. & Antonia, R. A. 2009 Momentum and heat transport in a three-dimensional transitional wake of a heated square cylinder. J. Fluid Mech. 640, 109–129.CrossRefGoogle Scholar
Geng, C., He, G., Wang, Y., Xu, C., Lozano-Durán, A. & Wallace, J. M. 2015 Taylor’s hypothesis in turbulent channel flow considered using a transport equation analysis. Phys. Fluids 27, 25111.CrossRefGoogle Scholar
George, W. & Hussein, H. 1991 Locally axisymmetric turbulence. J. Fluid Mech. 233, 1–23.CrossRefGoogle Scholar
Hammache, M. & Gharib, M. 1991 An experimental study of the parallel and oblique vortex shedding from circular cylinders. J. Fluid Mech. 232, 567–590.CrossRefGoogle Scholar
Hayakawa, M. & Hussain, F. 1985 Eduction of coherent structures in the turbulent plane wake. In Proc. 5th Symp. Turb. Shear Flows, Cornell Univ., pp. 4.33–4.37.Google Scholar
Hayakawa, M. & Hussain, F. 1989 Three-dimensionality of organized structures in a plane turbulent wake. J. Fluid Mech. 206, 375–404.CrossRefGoogle Scholar
Huang, J. F., Zhou, Y. & Zhou, T. 2006 Three-dimensional wake structure measurement using a modified PIV technique. Exp. Fluids 40, 884–896.CrossRefGoogle Scholar
Hussain, A. 1983 Coherent structures – reality and myth. Phys. Fluids 26, 2816–2850.CrossRefGoogle Scholar
Hussain, A. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.CrossRefGoogle Scholar
Hussain, A. & Hayakawa, M. 1987 Eduction of large-scale organized structures in a turbulent plane wake. J. Fluid Mech. 180, 193–229.CrossRefGoogle Scholar
Jeong, J., Grinstein, F. F. & Hussain, F. 1994 Eduction of coherent structures in a numerically simulated plane wake. Appl. Sci. Res. 53, 227–236.CrossRefGoogle Scholar
Kiya, M. & Matsumura, M. 1988 Incoherent turbulence structure in the near wake of a normal plate. J. Fluid Mech. 190, 343–356.CrossRefGoogle Scholar
Kolar, V., Lyn, D. A. & Rodi, W. 1997 Ensemble-averaged measurements in the turbulent near wake of two side-by-side square cylinders. J. Fluid Mech. 346, 201–237.CrossRefGoogle Scholar
Lefeuvre, N., Thiesset, F., Djenidi, L. & Antonia, R. A. 2014 Statistics of the turbulent kinetic energy dissipation rate and its surrogates in a square cylinder wake flow. Phys. Fluids 26, 95104.CrossRefGoogle Scholar
Li, N., Balaras, E. & Wallace, J. M. 2010 Passive scalar transport in a turbulent mixing layer. Flow Turbul. Combust. 85, 1–24.CrossRefGoogle Scholar
Marasli, B., Nguyen, P. & Wallace, J. M. 1993 A calibration technique for multiple-sensor hot-wire probes and its application to vorticity measurements in the wake of a circular cylinder. Exp. Fluids 15, 209–218.CrossRefGoogle Scholar
Matsumura, M. & Antonia, R. A. 1993 Momentum and heat transport in the turbulent intermediate wake of a circular cylinder. J. Fluid Mech. 250, 651–668.CrossRefGoogle Scholar
Mi, J. & Antonia, R. A. 1996 Vorticity characteristics of the turbulent intermediate wake. Exp. Fluids 20, 383–392.CrossRefGoogle Scholar
Mi, J. & Antonia, R. A. 2010 Approach to local axisymmetry in a turbulent cylinder wake. Exp. Fluids 48, 933–947.CrossRefGoogle Scholar
Ong, L. & Wallace, J. 1996 The velocity field of the turbulent very near wake of a circular cylinder. Exp. Fluids 20, 441–453.CrossRefGoogle Scholar
Pope, S. B. 2001 Turbulent Flows. Cambridge University Press.Google Scholar
Scarano, F. & Poelma, C. 2009 Three-dimensional vorticity patterns of cylinder wakes. Exp. Fluids 47, 69–83.CrossRefGoogle Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT press.CrossRefGoogle Scholar
Williamson, C. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.CrossRefGoogle Scholar
Wu, J., Sheridan, J., Welsh, M. C. & Hourigan, K. 1996 Three-dimensional vortex structures in a cylinder wake. J. Fluid Mech. 312, 2954–2964.CrossRefGoogle Scholar
Zaman, K. & Hussain, A. 1981 Taylor hypothesis and large-scale coherent structures. J. Fluid Mech. 112, 379–396.CrossRefGoogle Scholar
Zdravkovich, M. M. 1997 Flow Around Circular Cylinders: Volume 1: Fundamentals. Oxford University Press.CrossRefGoogle Scholar
Zhang, H. J., Zhou, Y. & Antonia, R. A. 2000 Longitudinal and spanwise vortical structures in a turbulent near wake. Phys. Fluids 12, 2954–2964.CrossRefGoogle Scholar
Zhou, T., Zhou, Y., Yiu, M. W. & Chua, L. P. 2003 Three-dimensional vorticity in a turbulent cylinder wake. Exp. Fluids 35, 459–471.CrossRefGoogle Scholar
Zhou, Y. & Antonia, R. A. 1992 Convection velocity measurements in a cylinder wake. Exp. Fluids 13, 63–70.CrossRefGoogle Scholar
Zhou, Y. & Antonia, R. A. 1994 Critical points in a turbulent near wake. J. Fluid Mech. 275, 59–82.CrossRefGoogle Scholar
Zhou, Y. & Yiu, M. W. 2006 Flow structure, momentum and heat transport in a two-tandem-cylinder wake. J. Fluid Mech. 548, 17–48.CrossRefGoogle Scholar
Zhou, Y., Zhang, H. J. & Yiu, M. W. 2002 The turbulent wake of two side-by-side circular cylinders. J. Fluid Mech. 458, 303–332.CrossRefGoogle Scholar