Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T17:39:44.829Z Has data issue: false hasContentIssue false
  • English
  • Français

The three-dimensional structure of momentum transfer in turbulent channels

Published online by Cambridge University Press:  02 February 2012

Adrián Lozano-Durán ,
Oscar Flores  and
Javier Jiménez
Adrián Lozano-Durán*
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, 28040 Madrid, Spain
Oscar Flores
Affiliation:
Department Mechanical Engineering, University of Washington Seattle, WA 98195, USA
Javier Jiménez
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, 28040 Madrid, Spain Centre for Turbulence Research, Stanford University, Stanford, CA 94305, USA
*
† Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The quadrant analysis of the intense tangential Reynolds stress in plane turbulent channels is generalized to three-dimensional structures (Qs), with special emphasis on the logarithmic and outer layers. Wall-detached Qs are background stress fluctuations. They are small and isotropically oriented, and their contributions to the mean stress cancel. Wall-attached Qs are larger, and carry most of the mean Reynolds stresses. They form a family of roughly self-similar objects that become increasingly complex away from the wall, resembling the vortex clusters in del Álamo et al. (J. Fluid Mech., vol. 561, 2006, pp. 329–358). Individual Qs have fractal dimensions of the order of 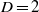, slightly fuller than the clusters. They can be described as ‘sponges of flakes’, while vortex clusters are ‘sponges of strings’. The number of attached Qs decays away from the wall, but the fraction of the stress that they carry is independent of their sizes. A substantial fraction of the stress resides in a few large objects extending beyond the centreline, reminiscent of the very large structures of several authors. The predominant logarithmic-layer structure is a side-by-side pair of a sweep (Q4) and an ejection (Q2), with an associated cluster, and shares dimensions and stresses with the conjectured attached eddies of Townsend (J. Fluid Mech., vol. 11, 1961, pp. 97–120). Those attached eddies tend to be aligned streamwise from each other, located near the side walls between the low- and high-velocity large-scale streaks, but that organization does not extend far enough to explain the very long structures in the centre of the channel.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 694 , 10 March 2012 , pp. 100 - 130
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.CrossRefGoogle Scholar
2. Adrian, R. J., Meinhart, C. D. & Tomkins, C. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
3. del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
4. del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.CrossRefGoogle Scholar
5. Antonia, R. A. & Atkinson, J. D. 1973 High-order moments of Reynolds shear stress fluctuations in a turbulent boundary layer. J. Fluid Mech. 58, 581–593.CrossRefGoogle Scholar
6. Antonia, R. A., Bisset, D. & Browne, L. 1990 Effect of Reynolds number on the topology of the organized motion in a turbulent boundary layer. J. Fluid Mech. 213, 267–286.CrossRefGoogle Scholar
7. Antonia, R. A. & Pearson, B. R. 1999 Low-order velocity structure functions in relatively high Reynolds number turbulence. Europhys. Lett. 48, 163–169.CrossRefGoogle Scholar
8. Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flow. Phil. Trans. R. Soc. A 365, 665–681.CrossRefGoogle Scholar
9. Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
10. Bermejo-Moreno, I. & Pullin, D. I. 2008 On the non-local geometry of turbulence. J. Fluid Mech. 603, 101–135.CrossRefGoogle Scholar
11. Blackburn, H. M., Mansour, N. N. & Cantwell, B. J. 1996 Topology of fine-scale motions in turbulent channel flow. J. Fluid Mech. 310, 269–292.CrossRefGoogle Scholar
12. Blackwelder, R. F. & Kaplan, R. E. 1976 On the wall structure of the turbulent boundary layer. J. Fluid Mech. 76, 89–112.Google Scholar
13. Bogard, D. G. & Tiederman, W. G. 1986 Burst detection with single-point velocity measurements. J. Fluid Mech. 162, 389–413.CrossRefGoogle Scholar
14. Corrsin, S. 1958 Local isotropy in turbulent shear flow. Res. Memo 58B11, NACA.Google Scholar
15. Dennis, D. J. C. & Nickels, T. B. 2011a Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1. Vortex packets. J. Fluid Mech. 673, 180–217.CrossRefGoogle Scholar
16. Dennis, D. J. C. & Nickels, T. B. 2011b Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures. J. Fluid Mech. 673, 218–244.CrossRefGoogle Scholar
17. Flores, O. & Jiménez, J. 2008 The structure of momentum transfer in turbulent channels. In Proceedings of Division Fluid Dynamics, pp. PA–08. American Physical Society.Google Scholar
18. Flores, O. & Jiménez, J. 2010a Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22, 071704.Google Scholar
19. Flores, O. & Jiménez, J. 2010b Log-layer dynamics in smooth and artificially rough turbulent channels. In IUTAM Symposium Physics of Turbulence over Rough Walls (ed. Nickels, T. ). pp. 93–98. Springer.CrossRefGoogle Scholar
20. Flores, O., Jiménez, J. & del Álamo, J. C. 2007 Vorticity organization in the outer layer of turbulent channels with disturbed walls. J. Fluid Mech. 591, 145–154.Google Scholar
21. Ganapathisubramani, B. 2008 Statistical structure of momentum sources and sinks in the outer region of a turbulent boundary layer. J. Fluid Mech. 606, 225–237.CrossRefGoogle Scholar
22. Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 33–46.Google Scholar
23. Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.CrossRefGoogle Scholar
24. Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to . Phys. Fluids 18, 011702.Google Scholar
25. Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 467–477.CrossRefGoogle Scholar
26. Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. A 365, 647–664.CrossRefGoogle ScholarPubMed
27. Hutchins, N., Monty, J. P., Ganapathisubramani, B., Ng, H. C. H. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.CrossRefGoogle Scholar
28. Jiménez, J. 1998 The largest scales of turbulence. In CTR Annals of Research Briefs, pp. 137–154. Stanford University.Google Scholar
29. Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.CrossRefGoogle Scholar
30. Jiménez, J., del Álamo, J. C. & Flores, O. 2004 The large-scale dynamics of near-wall turbulence. J. Fluid Mech. 505, 179–199.CrossRefGoogle Scholar
31. Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.Google Scholar
32. Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.CrossRefGoogle Scholar
33. Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.Google Scholar
34. Jiménez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.CrossRefGoogle Scholar
35. Kailas, S. V. & Narasimha, R. 1994 Similarity in vita-detected events in a nearly neutral atmospheric boundary layer. Proc. R. Soc. Lond. A 447, 211–222.Google Scholar
36. Katul, G., Poggi, D., Cava, D. & Finnigan, J. 2006 The relative importance of ejections and sweeps to momentum transfer in the atmospheric boundary layer. Boundary-Layer Meteorol. 120 (3), 367–375.Google Scholar
37. Kim, H. T., Kline, S. J. & Reynolds, W. C. 1971 The production of turbulence near a smooth wall in a turbulent boundary layer. J. Fluid Mech. 50, 133–160.CrossRefGoogle Scholar
38. Kim, J. 1985 Turbulence structures associated with the bursting event. Phys. Fluids 28, 52–58.Google Scholar
39. Kim, J., Moin, P. & Moser, R. D. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
40. Kim, K. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.Google Scholar
41. Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.CrossRefGoogle Scholar
42. Lee, S.-H. & Sung, H. J. 2011 Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 673, 80–120.Google Scholar
43. Lozano-Durán, A. & Jiménez, J. 2010 Time-resolved evolution of the wall-bounded vorticity cascade. In Proceedings of Division Fluid Dynamics, pp. EB–3. American Physical Society.Google Scholar
44. Lu, S. S. & Willmarth, W. W. 1973 Measurements of the structure of the Reynolds stress in a turbulent boundary layer. J. Fluid Mech. 60, 481–511.CrossRefGoogle Scholar
45. Meinhart, C. D. & Adrian, R. J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7, 694–696.CrossRefGoogle Scholar
46. Moisy, F. & Jiménez, J. 2004 Geometry and clustering of intense structures in isotropic turbulence. J. Fluid Mech. 513, 111–133.Google Scholar
47. Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to . Phys. Fluids 11, 943–945.CrossRefGoogle Scholar
48. Nagasoa, R. & Handler, R. A. 2003 Statistical analysis of coherent vortices near a free surface in a fully developed turbulence. Phys. Fluids 15 (2), 375–395.Google Scholar
49. Nakagawa, H. & Nezu, I. 1977 Prediction of the contributions to the Reynolds stress from bursting events in open-channel flows. J. Fluid Mech. 80, 99–128.Google Scholar
50. Narasimha, R., Kumar, S., Prabhu, A. & Kailas, S. V. 2007 Turbulent flux events in a nearly neutral atmospheric boundary layer. Phil. Trans. R. Soc. A 365 (1852), 841–858.CrossRefGoogle Scholar
51. Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
52. Raupach, M. R. 1981 Conditional statistics of Reynolds stress in rough-wall and smooth-wall turbulent boundary layers. J. Fluid Mech. 108, 363–382.CrossRefGoogle Scholar
53. Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601–639.CrossRefGoogle Scholar
54. Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary-layers at high Reynolds number. J. Fluid Mech. 268, 333–372.CrossRefGoogle Scholar
55. Spalart, P. R. 1988 Direct simulation of a turbulent boundary layer up to . J. Fluid Mech. 187, 61–98.CrossRefGoogle Scholar
56. Tanahashi, M., Kang, S., Miyamoto, T. & Shiokawa, S. 2004 Scaling law of fine scale eddies in turbulent channel flows up to . Intl J. Heat Fluid Flow 25, 331–341.Google Scholar
57. Tomkins, C. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
58. Townsend, A. A. 1961 Equilibrium layers and wall turbulence. J. Fluid Mech. 11, 97–120.CrossRefGoogle Scholar
59. Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
60. Van Atta, C. W. & Wyngaard, J. C. 1975 On higher-order spectra of turbulence. J. Fluid Mech. 72, 673–694.Google Scholar
61. Wallace, J. M., Eckelman, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54, 39–48.Google Scholar
62. Wark, C. E. & Nagib, H. M. 1991 Experimental investigation of coherent structures in turbulent boundary layers. J. Fluid Mech. 230, 183–208.Google Scholar
63. Willmarth, W. W. & Lu, S. S. 1972 Structure of the Reynolds stress near the wall. J. Fluid Mech. 55, 65–92.Google Scholar
64. Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar
Supplementary material: PDF

Lozano-Duran supplementary material

3D supplementary figure

Download Lozano-Duran supplementary material(PDF)
PDF 1.4 MB