Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T05:13:05.318Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional stability analysis for a salt-finger convecting layer

Published online by Cambridge University Press:  26 February 2018

Ting-Yueh Chang ,
Falin Chen Open the ORCID record for Falin Chen [Opens in a new window]  and
Min-Hsing Chang Open the ORCID record for Min-Hsing Chang [Opens in a new window]
Ting-Yueh Chang
Affiliation:
Institute of Applied Mechanics, National Taiwan University, Taipei, 106, Taiwan
Falin Chen*
Affiliation:
Institute of Applied Mechanics, National Taiwan University, Taipei, 106, Taiwan
Min-Hsing Chang
Affiliation:
Department of Mechanical Engineering, Tatung University, Taipei, 104, Taiwan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A three-dimensional linear stability analysis is carried out for a convecting layer in which both the temperature and solute distributions are linear in the horizontal direction. The three-dimensional results show that, for 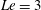$Le=3$ and 100, the most unstable mode occurs invariably as the longitudinal mode, a vortex roll with its axis perpendicular to the longitudinal plane, suggesting that the two-dimensional results are sufficient to illustrate the stability characteristics of the convecting layer. Two-dimensional results show that the stability boundaries of the transverse mode (a vortex roll with its axis perpendicular to the transverse plane) and the longitudinal modes are virtually overlapped in the regime dominated by thermal diffusion and the regime dominated by solute diffusion, while these two modes hold a significant difference in the regime the salt-finger instability prevails. More precisely, the instability area in terms of thermal Grashof number 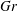$Gr$ and solute Grashof number 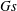$Gs$ is larger for the longitudinal mode than the transverse mode, implying that, under any circumstance, the longitudinal mode is always more unstable than the transverse mode.

JFM classification

Instability: Absolute/convective instability Convection: Buoyancy-driven instability Convection: Double diffusive convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 841 , 25 April 2018 , pp. 636 - 653
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bender, C. M. & Orszag, S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers. McGraw-Hill Book Co.Google Scholar
Biello, J. A. 1997 Aspects of double diffusion in a thin vertical slot. In Double Diffusive Processes, 1996 Summer Study Programme in Geophysical Fluid Dynamics, Woods Hole Oceanog. Inst. Tech. Rep., pp. 196–215. WHOI-97-10.Google Scholar
Chan, C. L., Chen, W. J. & Chen, C. F. 2002 Secondary motion in convection layers generated by lateral heating of a solute gradient. J. Fluid Mech. 455, 1–19.Google Scholar
Chen, C. F., Briggs, D. G. & Wirtz, R. A. 1971 Stability of thermal convection in a salinity gradient due to lateral heating. Intl J. Heat Mass Transfer 14, 57–65.Google Scholar
Chen, C. F. & Chan, C. L. 2010 Stability of buoyancy and surface tension driven convection in a horizontal double-diffusive fluid layer. Intl J. Heat Mass Transfer 53, 1563–1569.CrossRefGoogle Scholar
Chen, C. F. & Chen, F. 1997 Salt-finger convection generated by lateral heating of a solute gradient. J. Fluid Mech. 352, 161–176.Google Scholar
Dongarra, J. J., Straughan, B. & Walker, D. W. 1996 Chebyshev tau-qz algorithm methods for calculating spectra of hydrodynamic stability problems. Appl. Numer. Maths 22, 399–435.Google Scholar
Hart, J. E. 1972 Stability of thin non-rotating hadley circulation. J. Atmos. Sci. 29, 687–697.2.0.CO;2>CrossRefGoogle Scholar
Kerr, O. S. 1992 Two-dimensional instabilities of steady double-diffusive interleaving. J. Fluid Mech. 242, 99–116.Google Scholar
Kerr, O. S. 2000 Three-dimensional instabilities of steady double-diffusive interleaving. J. Fluid Mech. 418, 297–312.CrossRefGoogle Scholar
Kuo, H. P., Korpela, S. A., Chait, A. & Marcus, P. S. 1986 Stability of natural convection in a shallow cavity. In Eighth International Heat Transfer Conference, San Francisco, pp. 1539–1544. Hemisphere.Google Scholar
Malki-Epshtein, L., Phillips, O. M. & Huppert, H. E. 2004 The growth and structure of double-diffusive cells adjacent to a cooled sidewall in a salt-stratified environment. J. Fluid Mech. 518, 347–362.Google Scholar
Thorpe, S. A., Hutt, P. K. & Soulsby, R. 1969 The effects of horizontal gradients in thermohaline convection. J. Fluid Mech. 38, 375–400.CrossRefGoogle Scholar
Wirtz, R. A., Briggs, D. G. & Chen, C. F. 1972 Physical and numerical experiments on layered convection in a density-stratified fluid. Geophys. Fluid Dyn. 3, 265–288.Google Scholar