Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-08T22:04:33.794Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional Lagrangian Voronoï analysis for clustering of particles and bubbles in turbulence

Published online by Cambridge University Press:  06 January 2012

Yoshiyuki Tagawa ,
Julián Martínez Mercado ,
Vivek N. Prakash ,
Enrico Calzavarini ,
Chao Sun  and
Detlef Lohse
Yoshiyuki Tagawa*
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J.M. Burgers Center for Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands International Collaboration for Turbulence Research
Julián Martínez Mercado
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J.M. Burgers Center for Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands International Collaboration for Turbulence Research
Vivek N. Prakash
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J.M. Burgers Center for Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands International Collaboration for Turbulence Research
Enrico Calzavarini
Affiliation:
Laboratoire de Mécanique de Lille CNRS/UMR 8107, Université Lille 1 and Polytech’Lille, Cité Scientifique Av. P. Langevin, 59650 Villeneuve d’Ascq, France International Collaboration for Turbulence Research
Chao Sun*
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J.M. Burgers Center for Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands International Collaboration for Turbulence Research
Detlef Lohse*
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J.M. Burgers Center for Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands International Collaboration for Turbulence Research
*
†Email addresses for correspondence: [email protected], [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

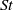Three-dimensional Voronoï analysis is used to quantify the clustering of inertial particles in homogeneous isotropic turbulence using data sets from numerics in the point particle limit and one experimental data set. We study the clustering behaviour at different density ratios, particle response times (i.e. Stokes numbers ) and two Taylor–Reynolds numbers ( 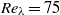and 180). The probability density functions (p.d.f.s) of the Voronoï cell volumes of light and heavy particles show different behaviour from that of randomly distributed particles, i.e. fluid tracers, implying that clustering is present. The standard deviation of the p.d.f. normalized by that of randomly distributed particles is used to quantify the clustering. The clustering for both light and heavy particles is stronger for higher 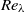. Light particles show maximum clustering for 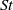around 1–2 for both Taylor–Reynolds numbers. The experimental data set shows reasonable agreement with the numerical results. The results are consistent with previous investigations employing other approaches to quantify the clustering. We also present the joint p.d.f.s of enstrophy and Voronoï volumes and their Lagrangian autocorrelations. The small Voronoï volumes of light particles correspond to regions of higher enstrophy than those of heavy particles, indicating that light particles cluster in higher vorticity regions. The Lagrangian temporal autocorrelation function of Voronoï volumes shows that the clustering of light particles lasts much longer than that of heavy or neutrally buoyant particles. Due to inertial effects arising from the density contrast with the surrounding liquid, light and heavy particles remain clustered for much longer times than the flow structures which cause the clustering.

JFM classification

Turbulent Flows: Homogeneous turbulence Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 693 , 25 February 2012 , pp. 201 - 215
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Aliseda, A., Cartellier, A., Hainaux, F. & Lasheras, J. C. 2002 Effect of preferential concentration on the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 468, 77–105.CrossRefGoogle Scholar
2. Bec, J., Biferale, L., Boffetta, G., Celani, A., Cencini, M., Lanotte, A., Musacchio, S. & Toschi, F. 2006 Acceleration statistics of heavy particles in turbulence. J. Fluid Mech. 550, 349–358.CrossRefGoogle Scholar
3. Benzi, R., Biferale, L., Calzavarini, E., Lohse, D. & Toschi, F. 2009 Velocity-gradient statistics along particle trajectories in turbulent flows: the refined similarity hypothesis in the Lagrangian frame. Phys. Rev. E 80 (6), 066318.CrossRefGoogle ScholarPubMed
4. Biferale, L., Scagliarini, A. & Toschi, F. 2010 On the measurement of vortex filament lifetime statistics in turbulence. Phys. Fluids 22, 065101.CrossRefGoogle Scholar
5. Bodenschatz, E., Malinowski, S. P., Shaw, R. A. & Stratmann, F. 2010 Can we understand clouds without turbulence? Science 327, 970–971.CrossRefGoogle ScholarPubMed
6. Calzavarini, E., van den Berg, T. H., Toschi, F. & Lohse, D. 2008a Quantifying microbubble clustering in turbulent flow from single-point measurements. Phys. Fluids 20, 040702.CrossRefGoogle Scholar
7. Calzavarini, E., Cencini, M., Lohse, D. & Toschi, F. 2008b Quantifying turbulence-induced segregation of inertial particles. Phys. Rev. Lett. 101, 084504.CrossRefGoogle ScholarPubMed
8. Calzavarini, E., Kerscher, M., Lohse, D. & Toschi, F. 2008c Dimensionality and morphology of particle and bubble clusters in turbulent flow. J. Fluid Mech. 607, 13–24.CrossRefGoogle Scholar
9. Chen, L., Goto, S. & Vassilicos, J. C. 2006 Turbulent clustering of stagnation points and inertial particles. J. Fluid Mech. 553, 143–154.CrossRefGoogle Scholar
10. Ferenc, J. S. & Néda, Z. 2007 On the size distribution of Poisson Voronoï cells. Physica A 385, 518–526.CrossRefGoogle Scholar
11. Fessler, J. R., Kulick, J. D. & Eaton, J. K. 1994 Preferential concentration of heavy particles in a turbulent channel flow. Phys. Fluids 6, 3742–3749.CrossRefGoogle Scholar
12. IJzermans, R. H. A., Reeks, M. W., Meneguz, E., Picciotto, M. & Soldati, A. 2009 Measuring segregation of inertial particles in turbulence by a full Lagrangian approach. Phys. Rev. E 80, 015302(R).CrossRefGoogle ScholarPubMed
13. Kerscher, M., Mecke, K., Schmalzing, J., Beisbart, C., Buchert, T. & Wagner, H. 2001 Morphological fluctuations of large-scale structure: the PSCz survey. Astron. Astrophys. 373, 1–11.CrossRefGoogle Scholar
14. Martinez Mercado, J., Chehata-Gomez, D., van Gils, D. P. M., Sun, C. & Lohse, D. 2010 On bubble clustering and energy spectra in pseudo-turbulence. J. Fluid Mech. 650, 287–306.CrossRefGoogle Scholar
15. Martinez Mercado, J., Prakash, V. N., Tagawa, Y., Sun, C. & Lohse, D. 2011 Lagrangian statistics of light particles in turbulence. Phys. Fluids (submitted), arXiv:1109.0188v1.Google Scholar
16. Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a non-uniform flow. Phys. Fluids 26, 883–889.CrossRefGoogle Scholar
17. Mazzitelli, I. M. & Lohse, D. 2004 Lagrangian statistics for fluid particles and bubbles in turbulence. New J. Phys. 6, 203.CrossRefGoogle Scholar
18. Mazzitelli, I. M., Lohse, D. & Toschi, F. 2003 On the relevance of the lift force in bubbly turbulence. J. Fluid Mech. 488, 283–313.CrossRefGoogle Scholar
19. Monchaux, R., Bourgoin, M. & Cartellier, A. 2010 Preferential concentration of heavy particles: a Voronoï analysis. Phys. Fluids 22, 103304.CrossRefGoogle Scholar
20. Okabe, A., Boots, B., Sugihara, K. & Chiu, S. N. 2000 Spatial Tesselations. Wiley.CrossRefGoogle Scholar
21. Pratsinis, S. E. & Vemury, S. 1996 Particle formation in gases: a review. Powder Technol. 88, 267–273.CrossRefGoogle Scholar
22. Saw, E. W., Shaw, R. A., Ayyalasomayajula, S., Chuang, P. Y. & Gylfason, A. 2008 Inertial clustering of particles in high-Reynolds-number turbulence. Phys. Rev. Lett. 100, 214501.CrossRefGoogle ScholarPubMed
23. Schmitt, F. G. & Seuront, L. 2008 Intermittent turbulence and copepod dynamics: increase in encounter rates through preferential concentration. J. Marine Syst. 70, 263–272.CrossRefGoogle Scholar
24. Toschi, F., Biferale, L., Calzavarini, E., Scagliarini, A. & Leveque, E. 2009 Lagrangian modelling and properties of particles with inertia. In Advances in Turbulence, XII, Proceedings of the 12th European Turbulence Conference (ETC-12), Marburg (D), Springer Proceedings in Physics.CrossRefGoogle Scholar
25. Toschi, F. & Bodenschatz, E. 2009 Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41, 375–404.CrossRefGoogle Scholar
26. van de Weygaert, R. & Icke, V. 1989 Fragmenting the universe. Part II. Voronoï vertices as Abell clusters. Astron. Astrophys. 213, 1–9.Google Scholar