Published online by Cambridge University Press: 03 June 2016
We investigate the early development of instabilities in the oscillatory viscous flow past cylinders with elliptic cross-sections using three-dimensional direct numerical simulations. This is a classical hydrodynamic problem for circular cylinders, but other configurations have received only marginal attention. Computed results for some different aspect ratios 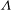 ${\it\Lambda}$ from 1 : 1 to 1 : 3, all with the major axis of the ellipse aligned in the main flow direction, show good qualitative agreement with Hall’s stability theory (J. Fluid Mech., vol. 146, 1984, pp. 347–367), which predicts a cusp-shaped curve for the onset of the primary instability. The three-dimensional flow structures for aspect ratios larger than 2 : 3 resemble those of a circular cylinder, whereas the elliptical cross-section with the lowest aspect ratio of 1 : 3 exhibits oblate rather than tubular three-dimensional flow structures as well as a pair of counter-rotating spanwise vortices which emerges near the tips of the ellipse. Contrary to a circular cylinder, instabilities for an elliptic cylinder with sufficiently high eccentricity emerge from four rather than two different locations in accordance with the Hall theory.
${\it\Lambda}$ from 1 : 1 to 1 : 3, all with the major axis of the ellipse aligned in the main flow direction, show good qualitative agreement with Hall’s stability theory (J. Fluid Mech., vol. 146, 1984, pp. 347–367), which predicts a cusp-shaped curve for the onset of the primary instability. The three-dimensional flow structures for aspect ratios larger than 2 : 3 resemble those of a circular cylinder, whereas the elliptical cross-section with the lowest aspect ratio of 1 : 3 exhibits oblate rather than tubular three-dimensional flow structures as well as a pair of counter-rotating spanwise vortices which emerges near the tips of the ellipse. Contrary to a circular cylinder, instabilities for an elliptic cylinder with sufficiently high eccentricity emerge from four rather than two different locations in accordance with the Hall theory.