Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T15:37:15.790Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional flow structures in laminar falling liquid films

Published online by Cambridge University Press:  04 March 2014

Georg F. Dietze Open the ORCID record for Georg F. Dietze [Opens in a new window] ,
W. Rohlfs ,
K. Nährich ,
R. Kneer  and
B. Scheid
Georg F. Dietze*
Affiliation:
Laboratoire FAST, CNRS, UPMC Université Paris 06, et Université Paris-Sud, Bâtiment 502, Campus Universitaire d’Orsay, 91405 Orsay, France
W. Rohlfs
Affiliation:
Institute of Heat and Mass Transfer, RWTH Aachen University, Aachen 52056, Germany
K. Nährich
Affiliation:
Institute of Heat and Mass Transfer, RWTH Aachen University, Aachen 52056, Germany
R. Kneer
Affiliation:
Institute of Heat and Mass Transfer, RWTH Aachen University, Aachen 52056, Germany
B. Scheid
Affiliation:
Laboratoire TIPs, Université Libre de Bruxelles, Bruxelles 1050, Belgium
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Full numerical simulations of the Navier–Stokes equations for four cases of vertically falling liquid films with three-dimensional surface waves have been performed. Flow conditions are based on several previous experimental studies where the streamwise and spanwise wavelengths were imposed, which we exploit by simulating periodic wave segments. The considered flows are laminar but approach conditions at which intermittent wave-induced turbulence has been observed elsewhere. Working liquids range from water to silicone oil and cover a large interval of the Kapitza number (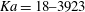$\textit {Ka}=18\mbox{--}3923$), which relates capillary to viscous forces. Simulations were performed on a supercomputer, using a finite-volume code and the volume of fluid and continuum surface force methods to account for the multiphase nature of the flow. Our results show that surface waves, consisting of large horseshoe-shaped wave humps concentrating most of the liquid and preceded by capillary ripples on a thin residual film, segregate the flow field into two regions: an inertia-dominated one in the large humps, where the local Reynolds number is up to five times larger than its mean value, and a visco-capillary region, where capillary and/or viscous forces dominate. In the inertial region, an intricate structure of different-scale vortices arises, which is more complicated than film thickness variations there suggest. Conversely, the flow in the visco-capillary region of large-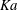$\textit {Ka} $ fluids is entirely governed by the local free-surface curvature through the action of capillary forces, which impose the pressure distribution in the liquid film. This results in flow separation zones underneath the capillary troughs and a spanwise cellular flow pattern in the region of capillary wave interference. In some cases, capillary waves bridge the large horseshoe humps in the spanwise direction, coupling the two aforementioned regions and leading the flow to oscillate between three- and two-dimensional wave patterns. This persists over long times, as we show by simulations with the low-dimensional model of Scheid et al. (J. Fluid Mech., vol. 562, 2006, pp. 183–222) after satisfactory comparison with our direct simulations at short times. The governing mechanism is connected to the bridging capillary waves, which drain liquid from the horseshoe humps, decreasing their amplitude and wave speed and causing them to retract in the streamwise direction. Overall, it is observed that spanwise flow structures (not accounted for in two-dimensional investigations) are particularly complex due to the absence of gravity in this direction.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Interfacial Flows (free surface): Thin films
Type
Papers
Information
Journal of Fluid Mechanics , Volume 743 , 25 March 2014 , pp. 75 - 123
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adomeit, P. & Renz, U. 2000 Hydrodynamics of three-dimensional waves in laminar falling films. Intl J. Multiphase Flow 26, 1183–1208.CrossRefGoogle Scholar
Alekseenko, S. V., Antipin, V. A., Guzanov, V. V., Kharlamov, S. M. & Markovich, D. M. 2005 Three-dimensional solitary waves on falling liquid film at low Reynolds numbers. Phys. Fluids 17, 121704.CrossRefGoogle Scholar
Alekseenko, S. V., Guzanov, V. V., Markovich, D. M. & Kharlamov, S. M. 2012 Specific features of a transition from the regular two-dimensional to three-dimensional waves on falling liquid films. Tech. Phys. Lett. 38 (8), 739–742.CrossRefGoogle Scholar
Alekseenko, S. V., Nakoryakov, V. E. & Pokusaev, B. G. 1994 Wave Flow of Liquid Films. Begell House.CrossRefGoogle Scholar
Boyd, J. P. 2001 Chebyshev and Fourier Spectral Methods. Courier Dover.Google Scholar
Brackbill, J. U., Kothe, D. B. & Zemach, C. 1992 A continuum method for modelling surface tension. J. Comput. Phys. 100, 335–354.CrossRefGoogle Scholar
Brauer, H. 1956 Strömung und Wärmebergang bei Rieselfilmen. VDI-Forschungsheft 457 (22), 1–40.Google Scholar
Brooke Benjamin, T. 1957 Wave formation in laminar flow down an inclined plane. J. Fluid Mech. 2, 554–574.CrossRefGoogle Scholar
Brooke Benjamin, T. 1961 The development of three-dimensional disturbances in an unstable film of liquid flowing down an inclined plane. J. Fluid Mech. 10, 401–419.CrossRefGoogle Scholar
Chang, H. C., Cheng, M., Demekhin, E. A. & Kopelevich, D. I. 1994 Secondary and tertiary excitation of three-dimensional patterns on a falling film. J. Fluid Mech. 270, 251–275.CrossRefGoogle Scholar
Chang, H. C., Demekhin, E. A. & Kalaidin, E. 1996a Simulation of noise-driven wave dynamics on a falling film. AIChE J. 42 (6), 1553–1568.CrossRefGoogle Scholar
Chang, H. C., Demekhin, E. A., Kalaidin, E. & Ye, Y. 1996b Coarsening dynamics of falling-film solitary waves. Phys. Rev. E 54 (2), 1467–1477.CrossRefGoogle ScholarPubMed
Chang, H. C., Demekhin, E. A. & Kopelevich, D. I. 1993 Nonlinear evolution of waves on a vertically falling film. J. Fluid Mech. 250, 433–480.CrossRefGoogle Scholar
Cheng, M. & Chang, H. C. 1995 Competition between subharmonic and sideband secondary instabilities on a falling film. Phys. Fluids 7 (1), 34–54.CrossRefGoogle Scholar
Cohen-Sabban, J., Gaillard-Groleas, J. & Crepin, P.-J. 2001 Quasi-confocal extended field surface sensing. In Optical Metrology Roadmap for the Semiconductor, Optical, and Data Storage Industries II (ed. Duparre, A. & Singh, B.), Proc. SPIE, vol. 4449, pp. 178–183. SPIE.CrossRefGoogle Scholar
Demekhin, E. A., Kalaidin, E. N., Kalliadasis, S. & Vlaskin, S. Yu. 2007a Three-dimensional localized coherent structures of surface turbulence. I. Scenarios of two-dimensional–three-dimensional transition. Phys. Fluids 19, 114103.Google Scholar
Demekhin, E. A., Kalaidin, E. N., Kalliadasis, S. & Vlaskin, S. Yu. 2007b Three-dimensional localized coherent structures of surface turbulence. II. Solitons. Phys. Fluids 19, 114104.Google Scholar
Demekhin, E. A., Kalaidin, E. N., Kalliadasis, S. & Vlaskin, S. Yu. 2010 Three-dimensional localized coherent structures of surface turbulence: model validation with experiments and further computations. Phys. Rev. E 82, 036322.CrossRefGoogle ScholarPubMed
Dietze, G. F., Al-Sibai, F. & Kneer, R. 2009 Experimental study of flow separation in laminar falling liquid films. J. Fluid Mech. 637, 73–104.CrossRefGoogle Scholar
Dietze, G. F., Leefken, A. & Kneer, R. 2008 Investigation of the back flow phenomenon in falling liquid films. J. Fluid Mech. 595, 435–459.CrossRefGoogle Scholar
Dietze, G. F. & Ruyer-Quil, C. 2013 Wavy liquid films in interaction with a confined laminar gas flow. J. Fluid Mech. 722, 348–393.CrossRefGoogle Scholar
Georgantaki, A., Vatteville, J., Vlachogiannis, M. & Bontozoglou, V. 2011 Measurements of liquid film flow as a function of fluid properties and channel width: evidence for surface-tension-induced long-range transverse coherence. Phys. Rev. E 84, 026325.CrossRefGoogle ScholarPubMed
Gjevik, B. 1970 Occurence of finite-amplitude surface waves on falling liquid films. Phys. Fluids 13 (8), 1918–1925.CrossRefGoogle Scholar
Hirt, C. W. & Nichols, B. D. 1981 Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 39, 201–225.CrossRefGoogle Scholar
Ishigai, S., Nakanisi, S., Koizumi, T. & Oyabu, Z. 1972 Hydrodynamics and heat transfer of vertically falling liquid films. Bull. JSME 15 (83), 594–601.CrossRefGoogle Scholar
Joo, S. W. & Davis, S. H. 1992 Instabilities of three-dimensional viscous falling films. J. Fluid Mech. 242, 529–547.CrossRefGoogle Scholar
Kalliadasis, S., Ruyer-Quil, C., Scheid, B. & Velarde, M. G. 2012 Falling Liquid Films. (Applied Mathematical Sciences) , vol. 176. Springer.CrossRefGoogle Scholar
Kapitza, P. L. 1948 Wave flow of thin layers of a viscous fluid. Zh. Eksp. Teor. Fiz. 3 (1), 3–28 (in Russian).Google Scholar
Kunugi, T. & Kino, C. 2005 DNS of falling film structure and heat transfer via MARS method. Comput. Struct. 83 (6–7), 455–462.CrossRefGoogle Scholar
Liu, J., Paul, J. D., Banilower, E. & Gollub, J. P. 1992 Film flow instabilities and spatiotemporal dynamics. In Proceedings of the First Experimental Chaos Conference (ed. Vohra, S., Spano, M., Schlesinger, M., Pecora, L. M. & Ditto, W.), pp. 225–239. World Scientific.Google Scholar
Liu, J., Paul, J. D. & Gollub, J. P. 1993 Measurements of the primary instabilities of film flows. J. Fluid Mech. 250, 69–101.CrossRefGoogle Scholar
Liu, J., Schneider, J. B. & Gollub, J. P. 1995 Three-dimensional instabilities of film flows. Phys. Fluids 7 (1), 55–67.CrossRefGoogle Scholar
Malamataris, N. A. & Balakotaiah, V. 2008 Flow structure underneath the large amplitude waves of a vertically falling film. AIChE J. 54 (7), 1725–1740.CrossRefGoogle Scholar
Malamataris, N. A., Vlachogiannis, M. & Bontozoglou, V. 2002 Solitary waves on inclined films: flow structure and binary interactions. Phys. Fluids 14 (3), 1082–1094.CrossRefGoogle Scholar
Manneville, P. 2004 Instabilities, Chaos and Turbulence. Imperial College Press.CrossRefGoogle Scholar
Miya, M., Woodmanee, D. E. & Hanratty, T. J. 1971 A model for roll waves in gas–liquid flow. Chem. Eng. Sci. 26, 1915–1931.CrossRefGoogle Scholar
Miyara, A. 1999 Numerical analysis on flow dynamics and heat transfer of falling liquid films with interfacial waves. Heat Mass Transfer 35, 298–306.CrossRefGoogle Scholar
Nave, J.-C.2004 Direct numerical simulation of liquid films. PhD thesis, University of California.Google Scholar
Nosoko, P., Yoshimura, P. N., Nagata, T. & Oyakawa, K. 1996 Characteristics of two-dimensional waves on a falling liquid film. Chem. Eng. Sci. 51 (5), 725–732.CrossRefGoogle Scholar
Nusselt, W. 1923 Der Wärmeaustausch am Berieselungskühler. Zeitschrift des VDI 67, 206–210.Google Scholar
Park, C. D. & Nosoko, T. 2003 Three-dimensional wave dynamics on a falling film and associated mass transfer. AIChE J. 49 (11), 2715–2727.CrossRefGoogle Scholar
Petviashvili, V. I. & Tsvelodub, D. Y. 1978 Horseshoe-shaped solitons on a flowing viscous film of fluid. Sov. Phys. Dokl. 23, 117–118.Google Scholar
Pollak, T., Haas, A. & Aksel, N. 2011 Side wall effects on the instability of thin gravity-driven films – from long-wave to short-wave instability. Phys. Fluids 23, 094110.CrossRefGoogle Scholar
Popinet, S. 2009 An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 228, 5838–5866.CrossRefGoogle Scholar
Pradas, M., Kalliadasis, S., Nguyen, P.-K. & Bontozoglou, V. 2013 Bound-state formation in interfacial turbulence: direct numerical simulations and theory. J. Fluid Mech. 716, R2.CrossRefGoogle Scholar
Pradas, M., Kalliadasis, S. & Tseluiko, D. 2012 Binary interactions of solitary pulses in falling liquid films. IMA J. Appl. Maths 77 (3), 408–419.CrossRefGoogle Scholar
Pradas, M., Tseluiko, D. & Kalliadasis, S. 2011 Rigorous coherent-structure theory for falling liquid films: viscous dispersion effects on bound-state formation and self-organization. Phys. Fluids 23, 044104.CrossRefGoogle Scholar
Press, W., Teukolsky, S., Vetterling, W. & Flannery, B. 1992 Numerical Recipes in C – The Art of Scientific Computing. Cambridge University Press.Google Scholar
Prosperetti, A. & Tryggvason, G.(Eds.) 2007 Computational Methods for Multiphase Flow. Cambridge University Press.CrossRefGoogle Scholar
Rohlfs, W., Dietze, G. F., Haustein, H., Tsvelodub, O. & Kneer, R. 2012 Experimental investigation into three-dimensional wavy liquid films under the influence of electrostatic forces. Exp. Fluids 53 (4), 1045–1056.CrossRefGoogle Scholar
Rusche, H.2002 Computational fluid dynamics of dispersed two-phase flows at high phase fractions. PhD thesis, Imperial College, University of London.Google Scholar
Ruyer-Quil, C. & Manneville, P. 2000 Improved modeling of flows down inclined planes. Eur. Phys. J. B 15 (2), 357–369.CrossRefGoogle Scholar
Ruyer-Quil, C. & Manneville, P. 2002 Further accuracy and convergence results on the modeling of flows down inclined planes by weighted-residual approximations. Phys. Fluids 14 (1), 170–183.CrossRefGoogle Scholar
Scheid, B., Kalliadasis, S., Ruyer-Quil, C. & Colinet, P. 2008a Interaction of three-dimensional hydrodynamic and thermocapillary instabilities in film flows. Phys. Rev. E 78, 066311.CrossRefGoogle ScholarPubMed
Scheid, B., Kalliadasis, S., Ruyer-Quil, C. & Colinet, P. 2008b Spontaneous channeling of solitary pulses in heated film flows. Europhys. Lett. 84 (6), 64002.CrossRefGoogle Scholar
Scheid, B., Ruyer-Quil, C. & Manneville, P. 2006 Wave patterns in film flows: modelling and three-dimensional waves. J. Fluid Mech. 562, 183–222.CrossRefGoogle Scholar
Shkadov, V. Ya. 1967 Wave flow regimes of a thin layer of viscous fluid subject to gravity. Fluid Dyn. 2 (1), 29–34.CrossRefGoogle Scholar
Squire, H. B. 1933 On the stability for three-dimensional disturbances of viscous fluid flow between parallel walls. Proc. R. Soc. Lond. A 142, 621–628.Google Scholar
Tailby, S. R. & Portalski, S. 1962 The determination of the wavelength on a vertical film of liquid flowing down a hydrodynamically smooth plate. Chem. Engng Res. Des. 40, 114–122.Google Scholar
Trifonov, Y. Y. 1990 Bifurcations of two-dimensional into three-dimensional wave regimes for a vertically flowing liquid film. Fluid Dyn. 25 (5), 741–745.CrossRefGoogle Scholar
Trifonov, Y. Y. 2012 Stability and bifurcations of the wavy film flow down a vertical plate: the results of integral approaches and full-scale computations. Fluid Dyn. Res. 44 (5), 031418.CrossRefGoogle Scholar
Vlachogiannis, M., Samandas, A., Leontidis, V. & Bontozoglou, V. 2010 Effect of channel width on the primary instability of inclined film flow. J. Fluid Mech. 22, 012106.Google Scholar
Youngs, D. L. 1982 Time-dependent multi-material flow with large fluid distortion. In Numerical Methods for Fluid Dynamics (ed. Morton, K. W. & Baines, M. J.), pp. 273–285. Academic Press.Google Scholar

Dietze et al. supplementary movie

DNS of case 1 (first line in tables 1-3 of manuscript): Re tgt=41, ftgt=19 Hz, Ka =3923, L=20 mm, W =10 mm. Time evolution of the velocity field projected onto a horizontal slice at the position of the trailing main wave hump.

Download Dietze et al. supplementary movie(Video)
Video 5 MB

Dietze et al. supplementary movie

DNS of case 1 (first line in tables 1-3 of manuscript): Retgt=41, ftgt=19 Hz, Ka=3923, L=20 mm, W=10 mm. Time evolution of the liquid-gas interface.

Download Dietze et al. supplementary movie(Video)
Video 2.4 MB

Dietze et al. supplementary movie

WRIBL model simulation of case 1 (first line in tables 1-3 of manuscript): Re tgt=41, f tgt=19 Hz, Ka. =3923, L=20 mm, W =10 mm. Time evolution of the liquid-gas interface.

Download Dietze et al. supplementary movie(Video)
Video 21 MB

Dietze et al. supplementary movie

DNS of case 2 (second line in tables 1-3 of manuscript): Retgt=59, f tgt=17 Hz, Ka =3923, L=25 mm, W =10 mm. Time evolution of the velocity field projected onto a horizontal slice at the position of the trailing main wave hump.

Download Dietze et al. supplementary movie(Video)
Video 7.2 MB

Dietze et al. supplementary movie

DNS of case 2 (second line in tables 1-3 of manuscript): Retgt=59, ftgt=17 Hz, Ka=3923, L=25 mm, W=10 mm. Time evolution of the liquid-gas interface.

Download Dietze et al. supplementary movie(Video)
Video 1.5 MB

Dietze et al. supplementary movie

WRIBL model simulation of case 2 (second line in tables 1-3 of manuscript): Re tgt=59, f tgt=17 Hz, Ka =3923, L=25 mm, W =10 mm. Time evolution of the liquid-gas interface.

Download Dietze et al. supplementary movie(Video)
Video 21.4 MB

Dietze et al. supplementary movie

DNS of case 3 (third line in tables 1-3 of manuscript): Retgt=15, ftgt=16 Hz, Ka=509.5, L=20.7 mm, W=10.35 mm. Time evolution of the liquid-gas interface.

Download Dietze et al. supplementary movie(Video)
Video 2.3 MB

Dietze et al. supplementary movie

WRIBL model simulation of case 3 (third line in tables 1-3 of manuscript) on a domain spanning two wavelengths in streamwise and spanwise directions: Re tgt=15, f tgt=16 Hz, Ka =509.5, L=20.7 mm, W=10.35 mm. Time evolution of film thickness contours (white: wave hump; black: wave trough).

Download Dietze et al. supplementary movie(Video)
Video 14 MB

Dietze et al. supplementary movie

WRIBL model simulation of case 3 (third line in tables 1-3 of manuscript): Re tgt=15, f tgt=16 Hz, Ka =509.5, L=20.7 mm, W =10.35 mm. Time evolution of the liquid-gas interface.

Download Dietze et al. supplementary movie(Video)
Video 9.4 MB

Dietze et al. supplementary movie

DNS of case 4 (fourth line in tables 1-3 of manuscript): Retgt=6, ftgt=17 Hz, Ka=17.8, L=22 mm, W=15 mm. Time evolution of the liquid-gas interface.

Download Dietze et al. supplementary movie(Video)
Video 1.1 MB

Dietze et al. supplementary movie

WRIBL model simulation of case 4 (fourth line in tables 1-3 of manuscript) on a domain spanning two wavelengths in streamwise and spanwise directions: Re tgt=6, f tgt=17 Hz, Ka=17.8, L=22 mm, W=15 mm. Time evolution of film thickness contours (white: wave hump; black: wave trough).

Download Dietze et al. supplementary movie(Video)
Video 13.7 MB

Dietze et al. supplementary movie

WRIBL model simulation of case 4 (fourth line in tables 1-3 of manuscript): Re tgt=6, f tgt=17 Hz, Ka=17.8, L=22 mm, W=15 mm. Time evolution of the liquid-gas interface.

Download Dietze et al. supplementary movie(Video)
Video 8.2 MB