Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T18:47:23.849Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional characteristics of the jet flows induced by a pitching plate in a quiescent fluid

Published online by Cambridge University Press:  28 January 2020

Navid Dehdari Ebrahimi Open the ORCID record for Navid Dehdari Ebrahimi [Opens in a new window] ,
Jeff D. Eldredge Open the ORCID record for Jeff D. Eldredge [Opens in a new window]  and
Y. Sungtaek Ju
Navid Dehdari Ebrahimi*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, Los Angeles, CA 90095, USA
Jeff D. Eldredge
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, Los Angeles, CA 90095, USA
Y. Sungtaek Ju*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, Los Angeles, CA 90095, USA
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

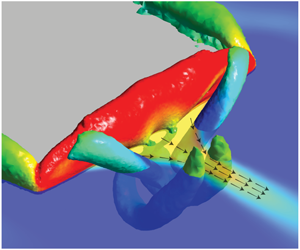
Jet flows induced by pitching cantilever plates provide a power-efficient solution for fluid acceleration and cooling enhancement. In such applications, the time-averaged (mean) properties of the induced jet flows are of great importance. We report a combined experimental and numerical study on the three-dimensional (3-D) characteristics of the mean jet downstream of a harmonically pitching cantilever plate in a quiescent fluid. These characteristics are then correlated with the transient 3-D vortex structures emanated from the trailing and side edges. Our particle image velocimetry and 3-D numerical simulations reveal that the mean induced jet has two distinct regions – a shrinking region immediately downstream of the trailing edge followed by an abrupt expansion region – separated by a necking point. We investigate the transient 3-D wake vortex evolution downstream of the plate to help elucidate the physics underlying the geometry of the mean jet. Our observations suggest that the breakdown of the shed vortex structure and reorientation of the consequent substructures are the primary factors governing the shape of the jet. These factors in turn are controlled primarily by the plate width and the amplitude of the oscillations. The results presented in this study improve our understanding of the complicated 3-D geometry of the induced mean jet in oscillating plates and facilitate optimal design of devices that operate based on this principle, such as piezoelectric fans.

JFM classification

Vortex Flows: Vortex dynamics Wakes/Jets: Jets Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 887 , 25 March 2020 , A25
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdelnour, K., Mancia, E., Peterson, S. D. & Porfiri, M. 2009 Hydrodynamics of underwater propulsors based on ionic polymer–metal composites: a numerical study. Smart Mater. Struct. 18 (8), 085006.CrossRefGoogle Scholar
Agarwal, A., Nolan, K. P., Stafford, J. & Jeffers, N. 2017 Visualization of three-dimensional structures shed by an oscillating beam. J. Fluids Struct. 70, 450–463.CrossRefGoogle Scholar
Asadzade, M. & Shamloo, A. 2017 Design and simulation of a novel bipolar plate based on lung-shaped bio-inspired flow pattern for pem fuel cell. Intl J. Energy Res. 41 (12), 1730–1739.CrossRefGoogle Scholar
Bidakhvidi, M. A., Shirzadeh, R., Steenackers, G. & Vanlanduit, S. 2013 Experimental study of the flow field induced by a resonating piezoelectric flapping wing. Exp. Fluids 54 (11), 1619.CrossRefGoogle Scholar
Bohl, D. G. & Koochesfahani, M. M. 2009 Mtv measurements of the vortical field in the wake of an airfoil oscillating at high reduced frequency. J. Fluid Mech. 620, 63–88.CrossRefGoogle Scholar
Buchholz, J. H. J.2006 The flowfield and performance of a low aspect ratio unsteady propulsor. PhD thesis, Princeton University.Google Scholar
Buchholz, J. H. J., Clark, R. P. & Smits, A. J. 2008 Thrust performance of unsteady propulsors using a novel measurement system, and corresponding wake patterns. Exp. Fluids 45 (3), 461–472.CrossRefGoogle ScholarPubMed
Buchholz, J. H. J. & Smits, A. J. 2005 Wake of a low aspect ratio pitching plate. Phys. Fluids 17 (9), 091102.CrossRefGoogle Scholar
Buchholz, J. H. J. & Smits, A. J. 2006 On the evolution of the wake structure produced by a low-aspect-ratio pitching panel. J. Fluid Mech. 546, 433–443.CrossRefGoogle Scholar
Buchholz, J. H. J. & Smits, A. J. 2008 The wake structure and thrust performance of a rigid low-aspect-ratio pitching panel. J. Fluid Mech. 603, 331–365.CrossRefGoogle ScholarPubMed
Choi, M., Cierpka, C. & Kim, Y.-H. 2012 Vortex formation by a vibrating cantilever. J. Fluids Struct. 31, 67–78.CrossRefGoogle Scholar
Cleaver, D. J., Wang, Z. & Gursul, I. 2012 Bifurcating flows of plunging aerofoils at high Strouhal numbers. J. Fluid Mech. 708, 349–376.CrossRefGoogle Scholar
Dewey, P. A., Boschitsch, B. M., Moored, K. W., Stone, H. A. & Smits, A. J. 2013 Scaling laws for the thrust production of flexible pitching panels. J. Fluid Mech. 732, 29–46.CrossRefGoogle Scholar
Eastman, A., Kiefer, J. & Kimber, M. 2012 Thrust measurements and flow field analysis of a piezoelectrically actuated oscillating cantilever. Exp. Fluids 53 (5), 1533–1543.CrossRefGoogle Scholar
Eastman, A. & Kimber, M. L. 2014 Aerodynamic damping of sidewall bounded oscillating cantilevers. J. Fluids Struct. 51, 148–160.CrossRefGoogle Scholar
Ebrahimi, N. D., Eldredge, J. D. & Ju, Y. S. 2019 Wake vortex regimes of a pitching cantilever plate in quiescent air and their correlation with mean flow generation. J. Fluids Struct. 84, 408–420.CrossRefGoogle Scholar
Ebrahimi, N. D., Wang, Y. & Ju, Y. S. 2018a Mechanisms of power dissipation in piezoelectric fans and their correlation with convective heat transfer performance. Sensors Actuators A 272, 242–252.CrossRefGoogle Scholar
Ebrahimi, N. D., Zeng, Z. & Ju, Y. S. 2018b Vortex propagation in air flows generated by piezoelectric fans and their correlation with fan cooling power efficiency. In International Heat Transfer Conference Digital Library. Begel House Inc.Google Scholar
Garcia, D. 2010 Robust smoothing of gridded data in one and higher dimensions with missing values. Comput. Stat. Data Analysis 54 (4), 1167–1178.CrossRefGoogle ScholarPubMed
Godoy-Diana, R., Marais, C., Aider, J.-L. & Wesfreid, J. E. 2009 A model for the symmetry breaking of the reverse Bénard–von Kármán vortex street produced by a flapping foil. J. Fluid Mech. 622, 23–32.CrossRefGoogle Scholar
Gravish, N., Peters, J. M., Combes, S. A. & Wood, R. J. 2015 Collective flow enhancement by tandem flapping wings. Phys. Rev. Lett. 115 (18), 188101.CrossRefGoogle ScholarPubMed
Green, M. A., Rowley, C. W. & Smits, A. J. 2011 The unsteady three-dimensional wake produced by a trapezoidal pitching panel. J. Fluid Mech. 685, 117–145.CrossRefGoogle Scholar
Green, M. A. & Smits, A. J. 2008 Effects of three-dimensionality on thrust production by a pitching panel. J. Fluid Mech. 615, 211–220.CrossRefGoogle ScholarPubMed
Hales, A. & Jiang, X. 2018 A review of piezoelectric fans for low energy cooling of power electronics. Appl. Energy 215, 321–337.CrossRefGoogle Scholar
Heathcote, S., Martin, D. & Gursul, I. 2004 Flexible flapping airfoil propulsion at zero freestream velocity. AIAA J. 42 (11), 2196–2204.CrossRefGoogle Scholar
Hussain, F. & Husain, H. S. 1989 Elliptic jets. Part 1. Characteristics of unexcited and excited jets. J. Fluid Mech. 208, 257–320.CrossRefGoogle Scholar
Jafari, P., Masoudi, A., Irajizad, P., Nazari, M., Kashyap, V., Eslami, B. & Ghasemi, H. 2018 Evaporation mass flux: a predictive model and experiments. Langmuir 34 (39), 11676–11684.CrossRefGoogle ScholarPubMed
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Jian, D. & Shao, X.-M. 2006 Hydrodynamics in a diamond-shaped fish school. J. Hydrodyn. B 18 (3), 438–442.Google Scholar
Khalid, M. S. U., Akhtar, I. & Dong, H. 2016 Hydrodynamics of a tandem fish school with asynchronous undulation of individuals. J. Fluids Struct. 66, 19–35.CrossRefGoogle Scholar
Kim, Y.-H., Cierpka, C. & Wereley, S. T. 2011 Flow field around a vibrating cantilever: coherent structure eduction by continuous wavelet transform and proper orthogonal decomposition. J. Fluid Mech. 669, 584–606.CrossRefGoogle Scholar
Kim, Y.-H., Wereley, S. T. & Chun, C.-H. 2004 Phase-resolved flow field produced by a vibrating cantilever plate between two endplates. Phys. Fluids 16 (1), 145–162.CrossRefGoogle Scholar
King, J. T. & Green, M. A. 2019 Experimental study of the three-dimensional wakes produced by trapezoidal panels with varying trailing edge geometry and pitching amplitude. In AIAA Scitech 2019 Forum, p. 1380.Google Scholar
Koochesfahani, M. M. 1989 Vortical patterns in the wake of an oscillating airfoil. AIAA J. 27 (9), 1200–1205.CrossRefGoogle Scholar
Koshigoe, S., Gutmark, E., Schadow, K. C. & Tubis, A. 1989 Initial development of noncircular jets leading to axis switching. AIAA J. 27 (4), 411–419.CrossRefGoogle Scholar
Krebs, F., Silva, F., Sciamarella, D. & Artana, G. 2012 A three-dimensional study of the glottal jet. Exp. Fluids 52 (5), 1133–1147.CrossRefGoogle Scholar
Krothapalli, A., Baganoff, D. & Karamcheti, K. 1981 On the mixing of a rectangular jet. J. Fluid Mech. 107, 201–220.CrossRefGoogle Scholar
Lighthill, M. J. 1971 Large-amplitude elongated-body theory of fish locomotion. Proc. R. Soc. Lond. B 179 (1055), 125–138.Google Scholar
Nazari, M., Masoudi, A., Jafari, P., Irajizad, P., Kashyap, V. & Ghasemi, H. 2018 Ultrahigh evaporative heat fluxes in nanoconfined geometries. Langmuir 35 (1), 78–85.CrossRefGoogle ScholarPubMed
Oh, M. H., Park, S. H., Kim, Y.-H. & Choi, M. 2018 3d flow structure around a piezoelectrically oscillating flat plate. Eur. J. Mech. (B/Fluids) 67, 249–258.CrossRefGoogle Scholar
Oh, M. H., Seo, J., Kim, Y.-H. & Choi, M. 2019 Endwall effects on 3d flow around a piezoelectric fan. Eur. J. Mech. (B/Fluids) 75, 339–351.CrossRefGoogle Scholar
Peterson, S. D., Porfiri, M. & Rovardi, A. 2009 A particle image velocimetry study of vibrating ionic polymer metal composites in aqueous environments. IEEE/ASME Trans. Mechatronics 14 (4), 474–483.CrossRefGoogle Scholar
Prince, C., Lin, W., Lin, J., Peterson, S. D. & Porfiri, M. 2010 Temporally-resolved hydrodynamics in the vicinity of a vibrating ionic polymer metal composite. J. Appl. Phys. 107 (9), 094908.CrossRefGoogle Scholar
Raspa, V., Ramananarivo, S., Thiria, B. & Godoy-Diana, R. 2014 Vortex-induced drag and the role of aspect ratio in undulatory swimmers. Phys. Fluids 26 (4), 041701.CrossRefGoogle Scholar
Schnipper, T., Andersen, A. & Bohr, T. 2009 Vortex wakes of a flapping foil. J. Fluid Mech. 633, 411–423.CrossRefGoogle Scholar
Shinde, S. Y. & Arakeri, J. H. 2014 Flexibility in flapping foil suppresses meandering of induced jet in absence of free stream. J. Fluid Mech. 757, 231–250.CrossRefGoogle Scholar
Shrestha, B., Ahsan, S. N. & Aureli, M. 2018 Experimental study of oscillating plates in viscous fluids: qualitative and quantitative analysis of the flow physics and hydrodynamic forces. Phys. Fluids 30 (1), 013102.CrossRefGoogle Scholar
Stafford, J. & Jeffers, N. 2017 Aerodynamic performance of a vibrating piezoelectric blade under varied operational and confinement states. IEEE Trans. Compon. Packag. Manufacturing Technol. 7 (5), 751–761.CrossRefGoogle Scholar
Taira, K. & Colonius, T. I. M. 2009 Three-dimensional flows around low-aspect-ratio flat-plate wings at low Reynolds numbers. J. Fluid Mech. 623, 187–207.CrossRefGoogle Scholar
Thielicke, W. 2014 The Flapping Flight of Birds: Analysis and Application. University of Groningen.Google Scholar
Thielicke, W. & Stamhuis, E. 2014 PIVlab – towards user-friendly, affordable and accurate digital particle image velocimetry in MATLAB. J. Open Res. Softw. 2 (1), e30; doi:http://doi.org/10.5334/jors.bl.CrossRefGoogle Scholar
Williamson, C. H. K. & Govardhan, R. 2008 A brief review of recent results in vortex-induced vibrations. J. Wind Engng Ind. Aerodyn. 96 (6–7), 713–735.CrossRefGoogle Scholar
Yuan, C., Liu, G., Ren, Y. & Dong, H. 2015 Propulsive performance and vortex interactions of multiple tandem foils pitching in line. In 45th AIAA Fluid Dynamics Conference, p. 3220.Google Scholar
Zaman, K. B. M. Q. 1996 Axis switching and spreading of an asymmetric jet: the role of coherent structure dynamics. J. Fluid Mech. 316, 1–27.CrossRefGoogle Scholar