Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T22:26:25.133Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional buoyancy-driven flow along a fractured boundary

Published online by Cambridge University Press:  09 July 2013

Adrian Farcas  and
Andrew W. Woods
Adrian Farcas
Affiliation:
BP Institute for Multiphase Flow, University of Cambridge, Madingly Road, Cambridge CB3 0EZ, UK
Andrew W. Woods*
Affiliation:
BP Institute for Multiphase Flow, University of Cambridge, Madingly Road, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe the steady motion of a buoyant fluid migrating through a porous layer along a plane, inclined boundary from a localized well. We first describe the transition from an approximately radially spreading current near the source, to a flow which runs upslope, as it spreads in the cross-slope direction. Using the model, we predict the maximum injection rate for which, near the source, the flow does not fully flood the porous layer. We then account for the presence of a fracture on the boundary through which some of the flow can drain upwards, and calculate how the current is partitioned between the fraction that drains and the remainder which continues running upslope. The fraction that drains increases with the permeability of the fracture and also with the distance from the source, as the flow slows and has more time to drain. We introduce new scalings and some asymptotic solutions to describe both the flow near the fracture and the three-dimensional surface of the injected fluid as it spreads upslope. We extend the model to the case of multiple fractures, so that the current eventually drains away as it flows over successive fractures. We calculate the shape of the region that is invaded by the buoyant fluid and we show that this flow, draining through a series of discrete fractures, may be approximated by a flow that continuously drains through its upper boundary. The effective small uniform permeability of this upper boundary is given by 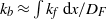${k}_{b} \approx \int \nolimits {k}_{f} \hspace{0.167em} \mathrm{d} x/ {D}_{F} $, where 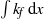$\int \nolimits {k}_{f} \hspace{0.167em} \mathrm{d} x$ is the integral of permeability across the width of the fracture and 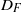${D}_{F} $ is the inter-fracture spacing. Finally, we discuss the relevance of the work for CO2 sequestration and we compare some simple predictions of the plume shape, volume and volume flux derived from our model with data from the Sleipner project, Norway for the plume of CO2 which developed in Horizon 1.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents Low-Reynolds-number flows: Low-Reynolds-number flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 728 , 10 August 2013 , pp. 279 - 305
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barenblatt, G. I. 1996 Scaling, Self-Similarity, and Intermediate Asymptotics. Cambridge University Press.Google Scholar
Bear, J. 1971 An Introduction to Flow in Porous Media. Wiley.Google Scholar
Bennion, B. & Bachu, S. 2006 The impact of interfacial tension and pore-size distribution/capillary pressure character on ${\mathrm{CO} }_{2} $ relative permeability at reservoir conditions in ${\mathrm{CO} }_{2} $ brine systems. SPE 99325. SPE/DOE Symposium on Improved Oil Recovery. Soc. of Petrol. Engrs.Google Scholar
Bickle, M., Chadwick, A., Huppert, H. E., Hallworth, M. & Lyle, S. 2007 Modelling carbon dioxide accumulation at Sleipner: implications for underground carbon storage. Earth Planet. Sci. Lett. 255, 164–176.CrossRefGoogle Scholar
Boait, F. C., White, N. J., Bickle, M. J., Chadwick, R. A., Neufeld, J. A. & Huppert, H. E. 2012 Spatial and temporal evolution of injected ${\mathrm{CO} }_{2} $ at the Sleipner field, North Sea. J. Geophys. Res. 117, B03309.Google Scholar
Chadwick, R. A., Arts, R. & Eiken, O. 2005 $\mathrm{4D} $ seismic imaging of a ${\mathrm{CO} }_{2} $ plume. In Petroleum Geology: North-West Europe and Global Perspectives, Proceedings of the 6th Petroleum Geology Conference (ed. A. G. Dore & B. A. Vining), pp. 1385–1399. Geological Society.Google Scholar
Dagan, G. & Neuman, S. P. (Eds) 1997 Subsurface Flow and Transport: A Stochastic Approach. Cambridge University Press.Google Scholar
Evans, J. P., Forster, C. B. & Goddard, J. V. 1997 Permeability of fault-related rocks, and implications for hydraulic structure of fault zones. J. Struct. Geol. 19, 1393–1404.CrossRefGoogle Scholar
Farcas, A. & Woods, A. W. 2009 The effect of drainage on the capillary retention of ${\mathrm{CO} }_{2} $ in a layered permeable rock. J. Fluid Mech. 618, 349–359.Google Scholar
Golding, M. J., Neufeld, J. A., Hesse, M. A. & Huppert, H. E. 2011 Two-phase gravity currents in porous media. J. Fluid Mech. 678, 248–270.Google Scholar
Gunn, I. & Woods, A. W. 2011 On the flow of buoyant fluid injected into a confined, inclined aquifer. J. Fluid Mech. 672, 109–129.Google Scholar
Hesse, M. A., Orr, F. M. Jr & Tchelepi, H. A. 2008 Gravity currents with residual trapping. J. Fluid Mech. 611, 35–60.Google Scholar
Hesse, M. A., Tchelepi, H. A., Cantwell, B. J. & Orr, F. M. Jr 2007 Gravity currents in horizontal porous layers: transition from early to late self-similarity. J. Fluid Mech. 577, 363–383.Google Scholar
Hesse, M. A., Tchelepi, H. A. & Orr, F. M. Jr 2006 Scaling analysis of the migration of ${\mathrm{CO} }_{2} $ in aquifers. SPE 102796. SPE Annual Technicl Conference and Exhibition, San Antonio. San Antonio.CrossRefGoogle Scholar
Homsy, G. M. 1987 Viscous fingering in porous media.. Annu. Rev. Fluid Mech. 19, 271–311.Google Scholar
Huppert, H. E. & Woods, A. W. 1995 Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69.Google Scholar
Juanes, R., Spiteri, E. J., Orr, F. M. Jr & Blunt, M. J. 2006 Impact of relative permeability hysteresis on geological ${\mathrm{CO} }_{2} $ storage. Water Resour. Res. 42, W12418.CrossRefGoogle Scholar
Lister, J. R. 1992 Viscous flows down an inclined plane from point and line sources. J. Fluid Mech. 242, 631–653.Google Scholar
de Loubens, R. & Ramakrishnan, T. 2011 Analysis and computation of gravity-induced migration in porous media. J. Fluid Mech. 675, 60–86.Google Scholar
Lovoll, G., Meheust, Y., Maloy, K. J., Aker, E. & Schmittbuhl, J. 2005 Competition of gravity, capillary and viscous forces, during drainage in a two-dimensional porous medium, a pore scale study. Energy 30, 861–872.Google Scholar
Lyle, S., Huppert, H. E., Hallworth, M., Bickle, M. & Chadwick, A. 2005 Axisymmetric gravity currents in a porous medium. J. Fluid Mech. 543, 293–302.CrossRefGoogle Scholar
Mitchell, V. & Woods, A. W. 2006 Gravity driven flow in confined aquifers. J. Fluid Mech. 566, 345–355.Google Scholar
Neufeld, J. A. & Huppert, H. E. 2009 Modelling carbon dioxide sequestration in layered strata. J. Fluid Mech. 625, 353–370.Google Scholar
Neufeld, J. A., Vella, D. & Huppert, H. E. 2009 The effect of a fissure on storage in a porous medium. J. Fluid Mech. 639, 239–259.Google Scholar
Neufeld, J. A., Vella, D., Huppert, H. E. & Lister, J. R. 2011 Leakage from gravity currents in a porous medium. Part 1. A localized sink. J. Fluid Mech. 666, 391–413.Google Scholar
Nordbotten, J. M. & Celia, M. A. 2006 Similarity solutions for fluid injection into confined aquifers. J. Fluid Mech. 561, 307–327.Google Scholar
Obi, E.-O. I. & Blunt, M. J. 2006 Streamline-based simulation of carbon dioxide storage in a North Sea aquifer. Water Resour. Res. 42, W03414.Google Scholar
Phillips, O. M. 1991 Flow and Reactions in Permeable Rocks. Cambridge University Press.Google Scholar
Pritchard, D. 2007 Gravity currents over fractured substrates in a porous medium. J. Fluid Mech. 584, 415–431.Google Scholar
Pritchard, D., Hogg, A. J. & Woods, A. W. 2001 On the slow draining of a gravity current moving through a layered permeable medium. J. Fluid Mech. 444, 23–47.Google Scholar
Pruess, K., Xu, T., Apps, J. A. & Garcia, J. 2003 Numerical modelling of aquifer disposal of ${\mathrm{CO} }_{2} $ . SPE J. 49–60.Google Scholar
Riaz, A., Hesse, M., Tchelepi, H. & Orr, F. M. Jr 2006 Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 548, 87–111.Google Scholar
Vella, D. & Huppert, H. E. 2006 Gravity currents in a porous medium at an inclined plane. J. Fluid Mech. 555, 353–362.Google Scholar
Vella, D., Neufeld, J. A., Huppert, H. E. & Lister, J. R. 2011 Leakage from gravity currents in a porous medium. Part 2. A line sink. J. Fluid Mech. 666, 414–427.Google Scholar
Verdon, J. & Woods, A. W. 2007 Gravity-driven reacting flows in a confined porous aquifer. J. Fluid Mech. 588, 29–41.Google Scholar
Woods, A. W. 1999 Liquid and vapour flow in superheated rock. Annu. Rev. Fluid Mech. 31, 171–199.Google Scholar
Woods, A. W. & Espie, T. 2012 Controls on the dissolution of ${\mathrm{CO} }_{2} $ plumes in structural traps in deep saline aquifers. Geophys Res. Lett. 39, L08401.Google Scholar
Woods, A. W. & Farcas, A. 2009 Capillary entry pressure and the leakage of gravity currents through a sloping layered permeable rock. J. Fluid Mech. 618, 361–379.Google Scholar
Woods, A. W. & Norris, S. 2010 On the role of caprock and fracture zones in dispersing gas plumes in the subsurface. Water Resour. Res. 46, W08522.Google Scholar
Yortsos, Y. C. 1995 A theoretical analysis of vertical flow equilibrium. Trans. Porous Med. 18, 107–129.CrossRefGoogle Scholar
Yortsos, Y. C. & Hickernell, F. J. 1989 Linear stability of immiscible displacement in porous media. SIAM J. Appl. Maths 49, 730–748.Google Scholar