Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Moll, R.
Garaud, P.
Mankovich, C.
and
Fortney, J. J.
2017.
Double-diffusive Erosion of the Core of Jupiter.
The Astrophysical Journal,
Vol. 849,
Issue. 1,
p.
24.
Taylor, J. R.
and
Zhou, Q.
2017.
A multi-parameter criterion for layer formation in a stratified shear flow using sorted buoyancy coordinates.
Journal of Fluid Mechanics,
Vol. 823,
Issue. ,
Garaud, P.
2017.
The formation of diffusive staircases.
Journal of Fluid Mechanics,
Vol. 812,
Issue. ,
p.
1.
Begeman, Carolyn Branecky
Tulaczyk, Slawek M.
Marsh, Oliver J.
Mikucki, Jill A.
Stanton, Timothy P.
Hodson, Timothy O.
Siegfried, Matthew R.
Powell, Ross D.
Christianson, Knut
and
King, Matt A.
2018.
Ocean Stratification and Low Melt Rates at the Ross Ice Shelf Grounding Zone.
Journal of Geophysical Research: Oceans,
Vol. 123,
Issue. 10,
p.
7438.
Garaud, Pascale
2018.
Double-Diffusive Convection at Low Prandtl Number.
Annual Review of Fluid Mechanics,
Vol. 50,
Issue. 1,
p.
275.
Brown, Justin M.
and
Radko, Timour
2019.
Initiation of diffusive layering by time-dependent shear.
Journal of Fluid Mechanics,
Vol. 858,
Issue. ,
p.
588.
Monville, R
Vidal, J
Cébron, D
and
Schaeffer, N
2019.
Rotating double-diffusive convection in stably stratified planetary cores.
Geophysical Journal International,
Vol. 219,
Issue. Supplement_1,
p.
S195.
Zaussinger, Florian
and
Kupka, Friedrich
2019.
Layer formation in double-diffusive convection over resting and moving heated plates.
Theoretical and Computational Fluid Dynamics,
Vol. 33,
Issue. 3-4,
p.
383.
Shibley, N. C.
and
Timmermans, M.‐L.
2019.
The Formation of Double‐Diffusive Layers in a Weakly Turbulent Environment.
Journal of Geophysical Research: Oceans,
Vol. 124,
Issue. 3,
p.
1445.
Radko, Timour
2019.
Thermohaline layering on the microscale.
Journal of Fluid Mechanics,
Vol. 862,
Issue. ,
p.
672.
Radko, Timour
and
Lewis, David
2019.
The age of a wake.
Physics of Fluids,
Vol. 31,
Issue. 7,
Radko, Timour
2019.
Instabilities of a Time-Dependent Shear Flow.
Journal of Physical Oceanography,
Vol. 49,
Issue. 9,
p.
2377.
Radko, Timour
2019.
Thermohaline‐Shear Instability.
Geophysical Research Letters,
Vol. 46,
Issue. 2,
p.
822.
Kupka, Friedrich
Zaussinger, Florian
Fabbian, Damian
and
Krüger, Daniel
2020.
The ANTARES code: recent developments and applications.
Journal of Physics: Conference Series,
Vol. 1623,
Issue. 1,
p.
012016.
Burin, M. J.
Sommeria, J.
and
Viboud, S.
2020.
Instabilities and layering of a heated laboratory anticyclone.
Physical Review Fluids,
Vol. 5,
Issue. 6,
Peltier, W. Richard
Ma, Yuchen
and
Chandan, Deepak
2020.
The KPP Trigger of Rapid AMOC Intensification in the Nonlinear Dansgaard‐Oeschger Relaxation Oscillation.
Journal of Geophysical Research: Oceans,
Vol. 125,
Issue. 5,
Garaud, P.
2021.
Journey to the center of stars: The realm of low Prandtl number fluid dynamics.
Physical Review Fluids,
Vol. 6,
Issue. 3,
Brown, Justin M.
and
Radko, Timour
2021.
ROME: A Pseudo‐Spectral Algorithm for Time‐Dependent Shear Flows in Stratified Environments.
Journal of Advances in Modeling Earth Systems,
Vol. 13,
Issue. 11,
Ma, Yuchen
and
Peltier, W. R.
2021.
Gamma instability in an inhomogeneous environment and salt-fingering staircase trapping: Determining the step size.
Physical Review Fluids,
Vol. 6,
Issue. 3,
Chang, Eonho
and
Garaud, Pascale
2021.
Modelling coexisting GSF and shear instabilities in rotating stars.
Monthly Notices of the Royal Astronomical Society,
Vol. 506,
Issue. 4,
p.
4914.
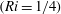 $(Ri=1/4)$ by up to four orders of magnitude. Direct numerical simulations indicate that these instabilities transform the initially linear density stratification into a series of well-defined horizontal layers. It is hypothesized that the combined thermohaline–shear instabilities could be ultimately responsible for the widespread occurrence of thermohaline staircases in diffusively stable regions of the World Ocean.
$(Ri=1/4)$ by up to four orders of magnitude. Direct numerical simulations indicate that these instabilities transform the initially linear density stratification into a series of well-defined horizontal layers. It is hypothesized that the combined thermohaline–shear instabilities could be ultimately responsible for the widespread occurrence of thermohaline staircases in diffusively stable regions of the World Ocean.


