Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T19:34:32.406Z Has data issue: false hasContentIssue false
  • English
  • Français

Thermoconvective instabilities of a non-uniform Joule-heated liquid enclosed in a rectangular cavity

Published online by Cambridge University Press:  23 March 2018

Franck Pigeonneau Open the ORCID record for Franck Pigeonneau [Opens in a new window] ,
Alexandre Cornet  and
Fredéric Lopépé
Franck Pigeonneau*
Affiliation:
MINES ParisTech, PSL Research University, CEMEF – Centre de mise en forme des matériaux, CNRS UMR 7635, CS 10207, 1 rue Claude Daunesse, 06904 Sophia Antipolis CEDEX, France
Alexandre Cornet
Affiliation:
Ecole normale supérieure Paris-Saclay, Université Paris-Saclay, 61 avenue du President Wilson, 94230 Cachan, France
Fredéric Lopépé
Affiliation:
ISOVER Saint-Gobain CRIR – BP 10019, 60291 Rantigny CEDEX, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Natural convection produced by a non-uniform internal heat source is studied numerically. Our investigation is limited to a two-dimensional enclosure with an aspect ratio equal to two. The energy source is Joule dissipation produced by an electric potential applied through two electrodes corresponding to a fraction of the vertical walls. The system of conservative equations of mass, momentum, energy and electric potential is solved assuming the Boussinesq approximation with a discontinuous Galerkin finite element method integrated over time. Three parameters are involved in the problem: the Rayleigh number 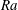$Ra$, the Prandtl number 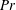$Pr$ and the electrode length 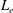$L_{e}$ normalized by the enclosure height. The numerical method has been validated in a case where electrodes have the same length as the vertical walls, leading to a uniform source term. The threshold of convection is established above a critical Rayleigh number, 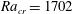$Ra_{cr}=1702$. Due to asymmetric boundary conditions on thermal field, the onset of convection is characterized by a transcritical bifurcation. Reduction of the size of the electrodes (from bottom up) leads to disappearance of the convection threshold. As soon as the electrode length is smaller than the cavity height, convection occurs even for small Rayleigh numbers below the critical value determined previously. At moderate Rayleigh number, the flow structure is mainly composed of a left clockwise rotation cell and a right anticlockwise rotation cell symmetrically spreading around the vertical middle axis of the enclosure. Numerical simulations have been performed for a specific 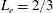$L_{e}=2/3$ with 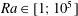$Ra\in [1;10^{5}]$ and 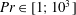$Pr\in [1;10^{3}]$. Four kinds of flow solutions are established, characterized by a two-cell symmetric steady-state structure with down-flow in the middle of the cavity for the first one. A first instability occurs for which a critical Rayleigh number depends strongly on the Prandtl number when 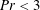$Pr<3$. The flow structure becomes asymmetric with only one steady-state cell. A second instability occurs above a second critical Rayleigh number that is quasiconstant when 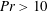$Pr>10$. The flow above the second critical Rayleigh number becomes periodic in time, showing that the onset of unsteadiness is similar to the Hopf bifurcation. When 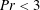$Pr<3$, a fourth steady-state solution is established when the Rayleigh number is larger than the second critical value, characterized by a steady-state structure with up-flow in the middle of the cavity.

JFM classification

Convection: Buoyancy-driven instability Convection: Convection in cavities
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 843 , 25 May 2018 , pp. 601 - 636
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1954 Heat transfer by free convection across a closed cavity between vertical boundaries at different temperatures. Q. Appl. Maths 12, 209–233.Google Scholar
Bergeon, A., Henry, D., Behadid, H. & Tuckerman, L. S. 1998 Marangoni convection in binary mixtures with Soret effect. J. Fluid Mech. 375, 143–177.Google Scholar
Chiu-Webster, S., Hinch, E. J. & Lister, J. R. 2008 Very viscous horizontal convection. J. Fluid Mech. 611, 395–426.Google Scholar
Choudhary, M. K. 1986 A three-dimensional mathematical model for flow and heat transfer in electrical glass furnaces. IEEE Trans. Ind. Appl. IA‐22 (5), 912–921.Google Scholar
Curran, R. L. 1971 Use of mathematical modeling in determining the effects of electrode configuration on convection currents in an electric glass melter. IEEE Trans. Ind. Applics. IGA‐7 (1), 116–129.Google Scholar
Curran, R. L. 1973 Mathematical model of an electric glass furnace: effects of glass color and resistivity. IEEE Trans. Ind. Applics. IA‐9 (3), 348–357.Google Scholar
Di Pietro, D. A. & Ern, A. 2012 Mathematical Aspects of Discontinuous Galerkin Methods. Springer.Google Scholar
Emara, A. A. & Kulacki, F. A. 1980 A numerical investigation of thermal convection in a heat-generating fluid layer. Trans. ASME J. Heat Transfer 102 (3), 531–537.Google Scholar
Flesselles, J.-M. & Pigeonneau, F. 2004 Kinematic regimes of convection at high Prandtl number in a shallow cavity. C. R. Méc. 332, 783–788.Google Scholar
Goluskin, D. 2016 Internally Heated Convection and Rayleigh–Bénard Convection. Springer.Google Scholar
Gopalakrishnan, S., Thess, A., Weidmann, G. & Lange, U. 2010 Chaotic mixing in a Joule-heated glass melt. Phys. Fluids 22 (1), 013101.Google Scholar
Gramberg, H. J. J., Howell, P. D. & Ockendon, J. R. 2007 Convection by a horizontal thermal gradient. J. Fluid Mech. 586, 41–57.Google Scholar
Joseph, D. D. 1976 Stability of Fluid Motions II. Springer.Google Scholar
Krishnamurti, R. 1973 Some further studies on the transition to turbulent convection. J. Fluid Mech. 60 (2), 285–303.Google Scholar
Kulacki, F. A. & Goldstein, R. J. 1975 Hydrodynamic instability in fluid layers with uniform volumetric energy sources. Appl. Sci. Res. 31 (2), 81–109.Google Scholar
Manneville, P. 2004 Instabilities, Chaos and Turbulence. World Scientific.Google Scholar
Pigeonneau, F. & Flesselles, J.-M. 2012 Practical laws for natural convection of viscous fluids heated from above in a shallow cavity. Intl J. Heat Mass Transfer 55, 436–442.Google Scholar
Roberts, P. H. 1967 Convection in horizontal layers with internal heat generation: theory. J. Fluid Mech. 30 (1), 33–49.Google Scholar
Ross, C. P. & Tincher, G. L. 2004 Glass Melting Technology: A Technical and Economic Assessment. Glass Manufacturing Industry Council.Google Scholar
Saramito, P. 2015a Efficient C++ Finite Element Computing with Rheolef. CNRS-CCSD.Google Scholar
Saramito, P. 2015b Efficient C++ Finite Element Computing with Rheolef, vol. 2: Discontinuous Galerkin Methods. CNRS-CCSD.Google Scholar
Saramito, P. 2016 Complex Fluids: Modeling and Algorithms, Mathématiques et Applications, vol. 79. Springer.Google Scholar
Scholze, H. 1990 Glass: Nature, Structures and Properties. Springer.Google Scholar
Stanek, J. 1977 Electric Melting of Glass. Elsevier.Google Scholar
Sugilal, G., Wattal, P. K. & Iyer, K. 2005 Convective behaviour of a uniformly Joule-heated liquid pool in a rectangular cavity. Intl J. Therm. Sci. 44, 915–925.Google Scholar
Süli, E. & Mayers, D. F. 2003 An Introduction to Numerical Analysis. Cambridge University Press.Google Scholar
Thirlby, R. 1970 Convection in an internally heated layer. J. Fluid Mech. 44 (4), 673–693.Google Scholar
Torres, J. F., Henry, D., Komiya, A. & Maruyama, S. 2014 Bifurcation analysis of steady natural convection in a tilted cubical cavity with adiabatic sidewalls. J. Fluid Mech. 756, 650–688.Google Scholar
Tritton, D. J. & Zarraga, M. N. 1967 Convection in horizontal layers with internal heat generation: experiments. J. Fluid Mech. 30 (1), 21–31.Google Scholar
Uguz, K. E., Labrosse, G., Narayanan, R. & Pigeonneau, F. 2014 From steady to unsteady 2-D horizontal convection at high Prandtl number. Intl J. Heat Mass Transfer 71, 469–474.Google Scholar
de Vahl Davis, G. 1983 Natural convection of air in a square cavity: a bench mark numerical solution. Intl J. Numer. Methods Fluids 3 (3), 249–264.Google Scholar
Viskanta, R. & Anderson, E. E. 1975 Heat transfer in semitransparent solids. Adv. Heat Transfer 11, 317–441.Google Scholar
Zeytounian, R. K. 2004 Theory and Applications of Viscous Fluid Flows. Springer.Google Scholar

Pigeonneau et al. supplementary movie

Temperature field for Pr=100 and Ra=40000

Download Pigeonneau et al. supplementary movie(Video)
Video 11.1 MB