Thermals from finite sources in stable and unstable environments

Abstract

The rise of thermals in the atmosphere has attracted a lot of attention since the early work of Morton et al. (Proc. R. Soc. Lond. A, vol. 234, 1956, pp. 1–23), who proposed that entrainment into a thermal was proportional to the surface area of the thermal and to the mean vertical velocity of the thermal. This paper presents new analytical solutions for the heights of rise of buoyant thermals in both stably and unstably stratified environments, for both negatively and positively buoyant sources, and where the sources have different size and strength (momentum) characteristics. The limiting cases of these analytical solutions are consistent with previous work. These analytical solutions do not appear elsewhere, and provide a compact set of equations that are easy to apply to a wide range of circumstances. The solutions are dependent upon the entrainment hypothesis, which is of course only an approximation, but the simplicity of the analytical solutions allows easy calculation and additional insights. These include the fact that while heights of rise are strongly dependent on both source strength and size for flows in stable environments, the dilution at the top of rise is independent of the source momentum. Further, in a stable environment, there is a conserved quantity that has dimensions proportional to vertical momentum. For negatively buoyant flows in an unstably stratified environment, thermals having low initial momentum will reach a maximum height, while thermals with high initial momentum will entrain sufficient buoyant environmental fluid that they will eventually become positively buoyant and continue to rise indefinitely.

1. Introduction

The pioneering work of Morton, Taylor & Turner (1956) established the basic equations governing the rise of buoyant plumes, jets and thermals. Asymptotic solutions were found for flows from point sources in stably and neutrally stratified environments, with dimensional reasoning governing the scaling. The present work details analytic solutions to those basic equations for thermals from sources that are of finite size and that possess momentum as well as buoyancy.

There are some basic assumptions of the pioneering work that are retained here, namely that density differences are sufficiently small that they appear only in buoyancy terms (the Boussinesq approximation), that as the thermal rises in an otherwise still environment it retains a self-similar spherical shape, and that the thermal entrains ambient fluid at a rate proportional to the product of the mean vertical velocity with the surface area. It is also assumed that there is no energy lost to the environment through internal waves, which would require an additional drag term as discussed by Bush, Thurber & Blanchette (2003).

There is a vast amount of more recent work on entrainment. For example, Kaminski, Tait & Carazzo (2005) discuss the fact that entrainment is reduced in negatively buoyant jets compared to those with positive buoyancy, and present a formulation for the entrainment constant based on the local Richardson number $Ri$. Ciriello & Hunt (2020) follow up on earlier work investigating the entrainment rate for plumes, also noting that $Ri$ plays an important role, and that entrainment rates differ for plumes from different source characteristics. A reduced rate of entrainment could well be the case for negatively buoyant thermals, and the dependence of entrainment on $Ri$ and on source characteristics for thermals may well be an issue, although no literature on this appears to be available. Shui & Weyl (1975) noted that form drag terms were small enough to be neglected, and that large thermals formed by strong explosions had entrainment parameters consistent with that found by Morton et al. (1956). However, most of these more recent works that provide potentially more accurate solutions still require numerical calculations, so that the fundamental first-order physics is perhaps less apparent.

There do not appear to be any publications that have investigated the effects of different source size and momentum on rate of rise. Orlandi & Carnevale (2020) undertook numerical simulations of thermal structure and rise in both stable and neutrally stratified environments. Their work focused on the internal vortex-ring-like structure and overall thermal shape that changes when impacting on a strong thermocline. There was no discussion of how the flow varies with differing source conditions. Domingos & Cardoso (2015) investigated the effects on rise of chemical reactions within a thermal, and noted that their analytic solutions for point sources converged to those of Morton et al. (1956). Makhviladze, Roberts & Yakush (1996) looked at buoyant thermal rise in a stratified atmosphere that had density inversely proportional to height. Unfortunately, their results are not comparable with the present work, which assumes that density decreases linearly with height.

Morton (1959) recognised that plumes having different strengths of source momentum and size (forced plumes) would result in flows of different characteristics near the source, and identified that jets with high momentum would have a more rapid entrainment near the source, so the angle of spread would be wider than that of a simple plume. Turner (1963a,b, 1964) further developed the theory for thermals, and later Turner (1966) established the flow characteristics of jets and plumes with negative or reversing buoyancy. Turner (1973) later provided a comprehensive review of buoyant plumes and thermals. Much of this work is well summarised in the monograph of Turner (1973).

With more extensive computing capability using the Fortran computing language, Morton & Middleton (1973) extended the work of Morton (1959) and provided a more detailed description of the possible flows of forced plumes. Later, Middleton (1979) realised that a change of independent variable from height of rise to time of rise would allow analytical solutions for times of rise of plumes, while the heights of rise remained to be determined numerically. Middleton (1986) recognised that full analytic solutions could be obtained for plumes in a crossflow using time of rise as the independent variable. Those basic equations and analytical solutions are extremely simple, if only approximate. Csanady (1980) briefly explored buoyant flows in unstable environments, noting that solutions for buoyancy and momentum for plumes in a crossflow had solutions that were comprised of hyperbolic functions.

In this paper, the application of the change of independent variable from height of rise to time of rise, as initiated by Middleton (1979, 1986) for forced plumes, is applied to thermals from sources of finite size and momentum. With this approach, analytical solutions for heights of rise and vertical velocity do indeed exist for thermals emitted into both stably stratified and unstably stratified environments for different source balance characteristics. These solutions do not seem to have been published elsewhere, and this paper presents the solutions as well as detailed descriptions of the flow characteristics for flows from sources of various strengths.

2. The thermal in a stably stratified environment

Turner (1973) pointed out that the circulation within a thermal has an influence on the dynamics of rise; however, a choice has been made here to limit the analysis to spherical thermals as distinct from buoyant vortex rings.

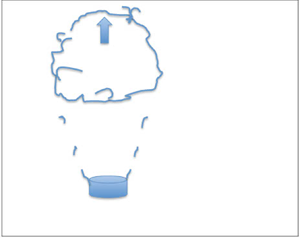
A schematic diagram of the thermal, and the basic mathematical variables used in the analyses below, are shown in figure 1.

Figure 1. Diagram showing the thermal radius $R$ at height $Z$, and the average vertical velocity $W$, with source values indicated by the zero subscript. The thermal and environmental densities are given by $\rho$ and $\rho _0$, respectively.

2.1. The equations

The equations are as described originally by Morton et al. (1956):

(2.1)$$\begin{gather} \frac{{\rm d} \tfrac43 {\rm \pi}R^3}{{\rm d} t} = 4 \alpha {\rm \pi}R^2 W, \end{gather}$$

(2.2)$$\begin{gather}\frac{{\rm d} {\rm \pi}R^3W}{{\rm d} t} = {\rm \pi}R^3 B, \end{gather}$$

(2.3)$$\begin{gather}\frac{{\rm d} {\rm \pi}R^3B}{{\rm d} t} =-{\rm \pi} R^3 W N^2. \end{gather}$$

Equation (2.1) describes the rate of increase of volume $\frac 43 {\rm \pi}R^3$ with time $t$ of the thermal, and assumes that the rate of entrainment across the thermal boundary is proportional to the surface area $4 {\rm \pi}R^2$ and to the mean thermal vertical velocity $W$, with the constant of proportionality being $\alpha$. Equation (2.2) expresses the rate of change of momentum as being proportional to the buoyancy force per unit mass

(2.4)\begin{equation} B = \frac{g (\rho_0 - \rho)}{\rho_1}. \end{equation}

Here, $\rho _1$ is the reference density, $\rho$ is the average density of fluid in the thermal, $\rho _0$ is the environment density at the same height as the thermal, and $g$ is the gravity constant. Equation (2.3) expresses how the buoyancy force per unit mass changes on entrainment of ambient fluid from the density stratified environment whose vertical density gradient (assumed constant) is expressed by

(2.5)\begin{equation} N^2 =-\frac{g}{\rho_1}\,\frac{{\rm d} \rho_0}{{\rm d} z}. \end{equation}

For a stable environment, $N^2 > 0$, and this is assumed for the rest of this section. In a later section, thermals in unstable environments will be considered, in which case the stratification will be defined with different sign. Now define bulk dimensional quantities that represent momentum $M$ and buoyancy $F$ as follows:

(2.6)$$\begin{gather} M = R^3 W, \end{gather}$$

(2.7)$$\begin{gather}F = R^3 B. \end{gather}$$

Equations (2.1)–(2.4) now appear as

(2.8)$$\begin{gather} \frac{{\rm d} R^3}{{\rm d} t} = \frac{3 \alpha M}{R}, \end{gather}$$

(2.9)$$\begin{gather}\frac{{\rm d} M}{{\rm d} t} = F, \end{gather}$$

(2.10)$$\begin{gather}\frac{{\rm d} F}{{\rm d} t} =- N^2 M. \end{gather}$$

With $M_0$ and $F_0$ designating the values at the source at time $t = 0$, the solutions to (2.9) and (2.10) are

(2.11)$$\begin{gather} M = M_0 \csc \delta \sin\theta, \end{gather}$$

(2.12)$$\begin{gather}F = F_0 \sec \delta \cos\theta, \end{gather}$$

where $\theta = N t +\delta$ is the phase angle, which increases with time as the thermal rises. With these definitions, it follows that the constant $\delta$ is defined by

(2.13)\begin{equation} \tan \delta = N M_0 /F_0. \end{equation}

The angle $\delta$ is therefore a measure of the relative influences of the time scale of the environmental stability $N$ and the source dimensions of momentum and buoyancy. The time $t= - N^{-1} \delta$, which occurs at $\theta = 0$, might be thought of as a virtual origin in time whereby the momentum is $M = 0$ and the buoyancy is given by $F = F_0 \sec \delta$. Using the definition of $\delta$ provides an alternative dimensional scaling for the momentum solution:

(2.14)\begin{equation} M = F_0 N^{-1} \sec\delta \sin\theta. \end{equation}

Equation (2.1) can be shown to simplify to ${\rm d} R/{\rm d} t =\alpha W$, and since the vertical velocity is $W = {\rm d} Z/{\rm d} t$, it follows that the spread of the thermal is linear with height $Z$ such that $R = R_0 + \alpha (Z-Z_0)$. Integrating (2.8) gives an expression for the radius $R$,

(2.15)\begin{equation} R^{4} = R_0^{4} + 4 \alpha \int_0^t M \,{\rm d} t, \end{equation}

and evaluating that integral using (2.10) gives

(2.16)\begin{equation} R^{4} = R_0^{4} + 4 \alpha N^{-2} (F_0 - F ). \end{equation}

At this stage, to simplify the presentation it is useful to define the dimensionless buoyancy $f$ as

(2.17)\begin{equation} f= \sec\delta \cos\theta, \end{equation}

and the dimensionless parameter $\varGamma$, which is a constant, as

(2.18)\begin{equation} \varGamma = \frac{ R_0^{4} N^2} {4 \alpha F_0}. \end{equation}

The parameter $\varGamma$ represents the balance of initial volume at the source, scaled with the length scale defined from the buoyancy and stratification. This $\varGamma$ may also be interpreted as the dimensionless source radius to the fourth power. The solution for the thermal radius at all times is given by

(2.19)\begin{equation} R^{4} = 4 \alpha F_0 N^{-2} (\varGamma+ 1 - f). \end{equation}

The dimensional height $Z-Z_0$ above the source is found by recognising the linear relationship $Z-Z_0=\alpha ^{-1} (R-R_0)$, and is

(2.20)\begin{equation} Z= 2^{1/2} (F_0 N^{-2} \alpha^{-3} )^{1/4 } ((\varGamma + 1 - f)^{1/4} - \varGamma^{1/4}). \end{equation}

The vertical velocity can be found either through the derivative of height $Z$ with respect to time, or more easily through the relationship (2.6), i.e. $W = MR^{-3}$.

These equations constitute the full analytical solutions for thermals being emitted vertically upwards into a density-stratified environment, with options for the source buoyancy being either positive or negative. For positively buoyant flows emitted upwards, $\delta$ lies in the range $0 < \delta < {\rm \pi}/2$, while for negatively buoyant flows emitted upwards, ${\rm \pi} /2 < \delta < {\rm \pi}$. A flow with initial positive buoyancy and positive momentum at the source has $\theta =\delta < {\rm \pi}/2$. As a positively buoyant thermal rises with time, the phase angle $\theta = N t +\delta$ grows, and when it approaches ${\rm \pi} /2$, the buoyancy drops to zero, but the momentum carries the thermal higher into the environment. Finally, at $\theta ={\rm \pi}$, the thermal reaches its maximum height. After this it will descend again towards equilibrium, continuing to entrain ambient fluid, but this further descent is not modelled here.

Limiting cases are found easily. For example, for neutral stratification and zero initial buoyancy, the asymptotic solutions for thermals emitted from a small origin come directly from (2.15) and are $R^4 = 4 \alpha M_0 t$ and $Z^4 = 4 \alpha ^{-3} M_0 t$.

For thermals emitted with finite $F_0$, consideration of (2.20) with $\varGamma$ negligible gives

(2.21)\begin{equation} Z^4 = 4 F_0 N^{-2} \alpha^{-3} (1 - f). \end{equation}

For small times, we have $1-f \approx \theta ^{2}/2 = N^2t^2/2$, the radius is given by $R^4 = 2 \alpha F_0 t^2$, and $Z^4 = 2 \alpha ^{-3} F_0 t^{2}$.

For the case of a point source ($\varGamma = 0$) of buoyancy only ($\delta = 0$) in a stratified environment, the solutions for $R$, $Z$, $F$ and $W$ are mathematically identical with those given by (20) of Morton et al. (1956). Results for the height of rise of a positively buoyant thermal can also be found easily, noting that the height of zero buoyancy is at $\theta ={\rm \pi} /2$ ($\,f = 0$), and the height of maximum rise is at $\theta ={\rm \pi}$ ($\,f = -1$). These asymptotic values are given by $Z^4= 4 F_0 N^2 \alpha ^{-3}$ and $Z^4= 8 F_0 N^2 \alpha ^{-3}$, respectively. Morton et al. (1956) give results for the maximum initial height of rise (their figure 7) as $X = 4.8$, and since $4.8/ 2^{3/2} \approx 1.68 \approx 8^{1/4}$, the present results are consistent, and the value of $\alpha$ from their experiments is $\alpha = 0.285$.

2.2. Calculating the solutions

For forced plumes Morton & Middleton (1973), following Morton (1959), chose to scale dimensionally using the initial momentum for their plume models, as this allowed focus on the role that the source strength balance plays on the resultant flow. For thermals in a stratified environment, it is perhaps more useful to scale the present analytical solutions with the environmental parameters $F_0$ and $N$, which will cater for graphical presentations covering a range of values of $F_0$ and $N$.

To allow for solutions that arise from either negatively or positively buoyant flows, it is useful to introduce the sign variable $sgn$ defined here by $F_0 = sgn\,|F_0|$ so that $sgn = +1$ for positively buoyant sources and $sgn = -1$ for negatively buoyant sources. The dimensionless solutions for each parameter can now be written in terms of a product of the scaling (which contains the dimensions and the entrainment parameter $\alpha$, but no numbers) and the numerical values of the equations and numerical multipliers.

The scaled solutions for momentum and buoyancy become

(2.22)$$\begin{gather} M/|F_0| = m = sgn \sec \delta \sin\theta, \end{gather}$$

(2.23)$$\begin{gather}F/|F_0| = f = sgn \sec \delta \cos\theta. \end{gather}$$

The radius becomes

(2.24)\begin{equation} R (N^2 / ( \alpha |F_0| ))^{1/4} = r = 4^{1/4} (\varGamma + sgn - f)^{1/4}, \end{equation}

and the height of the thermal above the source is given by

(2.25)\begin{equation} Z (N^2 /(\alpha^3 |F_0|))^{1/4} = z = 4^{1/4} ( ( \varGamma + sgn - f)^{1/4}) - \varGamma^{1/4}). \end{equation}

The vertical velocity is found from the relationship $w=m r^{-3}$ and has scaling $(|F_0| N^2/\alpha ^3)^{1/4}$.

For some applications, the rate of dilution of the effluent might be considered important. Defining this as the ratio of volume flux at height to that at the source, the dilution is $D = ((\varGamma + 1 - f)/\varGamma )^{3/4}$ for a thermal in a stably stratified environment. As $f = -1$ at the top of rise, the dilution there is $D = (1 + 2/\varGamma )^{3/4}$.

2.3. Describing the solutions

Before proceeding with the discussion, it is important to recognise the structure of the equations. The source buoyancy flux $F_0$ and the environmental stratification $N$ are used to create the dimensional scaling of the equations. The numerical results therefore cannot explicitly depict the way in which the flows might eventuate as a consequence of changes in either of those parameters. Instead, the dependence on the source characteristics (volume and momentum) can be determined readily with this approach.

The parameter $\varGamma$ may be thought of as representing the source volume, which is proportional to $R_0 ^3$, suitably made dimensionless with the source buoyancy and environmental stratification. Smaller values of $\varGamma$ represent small radius sources, while larger values represent sources of larger extent. The solutions for $\varGamma =0$ are those for point sources that were found by Morton et al. (1956) and are shown in their (20) and (21).

The parameter $\delta$ may be thought of as representing the source momentum, suitably made dimensionless with the source buoyancy and environmental stratification. Small values represent sources with low momentum, while a value $\delta = {\rm \pi}/2$ represents a source of infinite momentum (clearly unrealistic). However, flows for which $\delta$ approaches ${\rm \pi} /2$ from below have high source momentum and positive source buoyancy, while flows for which $\delta$ exceeds ${\rm \pi} /2$ by a small amount have high source momentum but negative source buoyancy.

The results for thermals are shown in figure 2. Figure 2(a) is for a positively buoyant source and shows the various dimensionless variables $m$ (momentum), $f$ (buoyancy), $w$ (velocity), $r$ (radius) and $z$ (height), for $\varGamma = 0.2$ and $\delta = 0.2$, plotted as functions of time represented by $\theta$. The buoyancy $f$ drops from a value near 1 at the source to zero at $\theta ={\rm \pi} /2$, and then to $f = -1$ at $\theta = {\rm \pi}$. The momentum $m$ rises from its source value $\tan \delta$ at $\theta = \delta$ to a maximum value 1, then decreases to zero at $\theta ={\rm \pi}$. The vertical velocity $w$ rises rapidly at first then decays once the entrainment has added sufficient extra volume, before reaching zero buoyancy at $\theta = {\rm \pi}/2$. The height $z$ and radius $r$ have the same shape, with the vertical source at $z = 0$ and the source radius $r$ reflected by $\varGamma$.

Figure 2. The momentum $m$, buoyancy $f$, radius $r$, vertical velocity $w$ and height of rise $z$ for selected values of parameters $\varGamma$ and $\delta$ for both positively and negatively buoyant thermals in a stably stratified environment.

Figure 2(b) shows the same plume variables as in figure 2(a), but now arising from a negatively buoyant source at $\delta =1.8$, after which the buoyancy satisfies $f < 0$ and continues to decrease. The vertical velocity starts at its maximum value at the source, then drops as the negative buoyancy retards the flow. Figure 2(c) shows heights of rise for specific source size $\varGamma = 0.2$ and for various values of $\delta$. For low values of $\delta$, the heights of rise are modest and rise as the source momentum increases (higher $\delta$). Beyond $\delta = {\rm \pi}/2$, the negative buoyancy of the source has the effect of reducing the rate of rise $w$ and limiting the height of rise $z$.

Figure 2(d) shows, for $\delta =0.2$ and $\delta =1.8$, how the heights of rise vary with $\varGamma$. Higher values of $\varGamma$ result in lower maximum heights as the sources with larger radius create a larger thermal so that the buoyancy per unit volume is lower and the vertical velocity is lower.

Considering solutions (2.11) and (2.12), the quantity

(2.26)\begin{equation} Q^2= M^2+N^{-2}F^2 = N^{-2}F_0^2 \sec^2 \delta \end{equation}

is a positive flow constant independent of time as the thermal rises. The dimensions of $Q$ are that of volume times velocity, hence $Q$ is in effect a conserved specific vertical momentum. For $\delta < {\rm \pi}/2$, both $M_0$ and $F_0$ are positive at the origin, and momentum increases as the relative buoyancy drops. For $M_0 > 0$, $F_0 < 0$ as the buoyancy becomes increasingly negative, and the momentum drops from its initial (and highest) value.

These results will be compared to those for thermals emitted into an unstably stratified environment in the next two sections.

3. The thermal in an unstably stratified environment

The same formulation is used as in § 2. Equations (2.1) and (2.2) remain valid, while (2.3) has a sign change in the stratification, so that (2.3) is replaced by

(3.1)\begin{equation} \frac{{\rm d} {\rm \pi}R^3B}{{\rm d} t} = {\rm \pi}R^3 W G^2, \end{equation}

where

(3.2)\begin{equation} G^2= \frac{g}{\rho_1}\,\frac{{\rm d} \rho_0}{{\rm d} z}. \end{equation}

Here, $G$ clearly takes on the same role for the unstable environment as did $N$ for the stable environment.

The bulk quantities that represent momentum $M$ and buoyancy $F$ are as defined in § 2. Solutions to (2.2) and (2.3) are

(3.3)$$\begin{gather} M/ M_0 = \cosh \theta + \epsilon ^{-1} \sinh \theta, \end{gather}$$

(3.4)$$\begin{gather}F/ F_0 = \cosh \theta + \epsilon \sinh \theta. \end{gather}$$

Here, $\epsilon$ is defined by

(3.5)\begin{equation} \epsilon = G M_0 / F_0 \end{equation}

in analogy with (2.12). The phase angle representing dimensionless time is now given by $\theta = Gt$. By virtue of the definition of $\epsilon$, the dimensionless definitions of momentum and buoyancy are

(3.6)\begin{equation} M G/F_0 = m = \epsilon \cosh\theta + \sinh\theta \end{equation}

and

(3.7)\begin{equation} F/ F_0 = f = \cosh \theta + \epsilon \sinh \theta. \end{equation}

The equation for the radius is $R^{4} = R_0^{4} + 4 \alpha \int _0^t M \,{\rm d} t$ as before, and evaluating the integral yields

(3.8)\begin{equation} R^{4} G^2/ ( \alpha F_0) = r^4 = 4(\varGamma + f - 1), \end{equation}

where the dimensionless source parameter $\varGamma$ is now defined by

(3.9)\begin{equation} \varGamma= \frac{R_0^{4} G^2} {4 \alpha F_0 }. \end{equation}

The height of rise is given by

(3.10)\begin{equation} Z^4 G^2/ ( \alpha^3 F_0) = z = 2^{1/2} ( (\varGamma + f - 1 )^{1/4} - \varGamma^{1/4} ). \end{equation}

The vertical velocity is found from the relationship $w = m r^{-3}$ and has scaling $(|F_0| G^2/\alpha ^3)^{1/4}$.

3.1. Calculating the solutions

In analogy with § 2, we will consider solutions for both positively and negatively buoyant flows rising into an unstable environment. Define the sign of the buoyancy $F_0$ by $sgn$, i.e. $F_0 = sgn\,|F_0|$, and $\epsilon = G M_0/|F_0|$. The dimensionless equations are

(3.11)$$\begin{gather} m = \epsilon \cosh\theta + sgn \sinh\theta, \end{gather}$$

(3.12)$$\begin{gather}f = sgn \cosh\theta+ \epsilon \sinh\theta, \end{gather}$$

(3.13)$$\begin{gather}r = 2 ^{1/2}( \varGamma + f - sgn)^{1/4}, \end{gather}$$

(3.14)$$\begin{gather}z = 2 ^{1/2} ( (\varGamma + f - sgn)^{1/4} - \varGamma^{1/4} ), \end{gather}$$

(3.15)$$\begin{gather}w = m/r^3. \end{gather}$$

3.2. Describing the solutions

The case of a positive thermal emitted into an unstable environment is straightforward in that all properties increase hyperbolically with time. This may occur in very limited circumstances where, for example, there is rapid heating of the Earth's surface in the morning as might occur when cloud cover is non-existent, and the morning sun rapidly heats the surface of the Earth, which has cooled substantially overnight. It might also occur at times when cooler air flows over a warmer surface. Such circumstances are almost certain to be brief, limited perhaps to a few hours of the day. Nevertheless, this theory will cater for those circumstances. Figure 3(a) shows the parameters $r$, $b$ and $w$ as functions of time for $\varGamma = 0.2$ and $\epsilon = 1.2$. Figure 3(b) shows heights of rise as a function of time ($\theta = Gt$) for $\epsilon = 2.2$ and various values of $\varGamma$. As for thermals in a stable environment, smaller thermals rise more rapidly as their entrainment rate is slower than for larger thermals.

Figure 3. Plots showing the momentum $m$, buoyancy $f$, radius $r$, vertical velocity $w$ and height of rise $z$ for selected values of parameters $\varGamma$ and $\epsilon$ for positively buoyant thermals in an unstably stratified environment.

A more interesting situation occurs when a negatively buoyant thermal is projected into an unstably stratified atmosphere. There are two possibilities, both of which are catered for by the theory. One case occurs when the source momentum is large enough to continue the thermal rise up to the point where entrainment of lighter fluid changes the sign of the thermal buoyancy from negative to positive (with respect to the local environment at that height). In this case, the thermal's vertical velocity slows at first, then ultimately accelerates upwards once more under its newly found positive buoyancy. The second case arises when the initial source momentum is weak, and entrainment of less dense environmental fluid is insufficient to change the sign of the thermal buoyancy before it ceases to rise.

Figure 4(a) shows the dimensionless parameters as a function of angle $\theta$, which is dimensionless time. Note that the phase origin for these calculations is always zero. The dimensionless parameters are plotted against $\theta$ for specific values of $\varGamma = 0.2$, and $\epsilon = 1.2$. This reflects a negatively buoyant source of relatively small radius emitting into an unstable environment. Both height and radius grow rapidly at first, then the growth is slowed down as entrainment dilutes the thermal. The momentum drops initially as the negative buoyancy impacts the flow, and the buoyancy increases from $f = -1$ as more positively buoyant fluid is entrained. At about $\theta \approx 1.2$, the buoyancy changes sign and becomes positive, and the momentum starts to increase again from its minimum value. It takes a little longer for the vertical velocity to begin increasing again because $m = b^3w$, and the radius is growing at the time when $m = 0$. Ultimately, the unstable environment controls the growth, and both momentum and buoyancy increase at a more rapid rate as time progresses.

Figure 4. Plots showing the momentum $m$, buoyancy $f$, radius $r$, vertical velocity $w$ and height of rise $z$ for selected values of parameters $\varGamma$ and $\epsilon$ for negatively buoyant thermals in a unstably stratified environment.

The criterion that indicates whether a thermal will continue to grow or to reach a maximum height is determined by $m = 0$. This occurs when $\tanh \theta = \epsilon = G W_0/ |B|$. Since $\tanh \theta$ can never exceed 1, a maximum height is never reached if $\epsilon > 1$. Maximum heights are reached only when $\epsilon < 1$, because the source velocity is sufficiently high, and the height is given by evaluating $\theta _m = \tanh ^{-1} \epsilon$, then using that value to calculate $f$ and $z$. For the limiting case $\epsilon = 1$, the thermal reaches a level of neutral buoyancy and neutral momentum asymptotically for large time.

Figure 4(b) shows the dimensionless parameters plotted for values of $\varGamma = 0.2$, and $\epsilon = 0.98$. This reflects a negatively buoyant source of small radius emitting into an unstable environment with insufficient momentum, and in this case the thermal reaches its maximum height with zero momentum and zero vertical velocity. The buoyancy $f$ remains negative at all times.

Figure 4(c) shows heights for rise for $\varGamma = 0.2$ and for various $\epsilon$. Growth is most rapid for larger values of $\epsilon > 1$, reflecting a stronger source momentum, while for $\epsilon = 1$, the maximum height is reached asymptotically for large $\theta$. For $\epsilon < 1$, the maximum height is reached, and beyond that time, calculations are not presented.

Figure 4(d) examines the dependence of the height of rise on $\varGamma$ for the selected value $\epsilon = 2.2$, reflecting a continuing rise at all times. As with thermals in a stable environment, a larger $\varGamma$ ensures a greater relative rate of entrainment and a slower rate of rise.

4. General discussion

There is a considerable literature refining the concepts of turbulence and entrainment for buoyant flows. The overall Richardson number $Ri = F (WR)^{-2}$ for the asymptotic solutions of thermals in a neutral environment is constant (as is true for pure plumes); however, this is not the case for either flow in a stable environment. This remains a limiting factor for the present analyses, which rely on the entrainment rate to depend only on the vertical velocity and not on $Ri$ for non-neutral environments, despite this being a known factor for plumes as described by Ciriello & Hunt (2020).

For the present results, the scaling is undertaken with buoyancy $F_0$ and stratification $N$ (or $G$ in the case of unstably stratified environments) as the key dimensional parameters. The entrainment constant $\alpha$ is included in the dimensional grouping so that the numerical dimensionless solutions are independent of the numerical value of $\alpha$. For thermals, heights of rise are proportional to $(\alpha F_0 N^{-2})^{1/4}$ so that the height of rise is inversely proportional to $- {\rm d} \rho _0 /{\rm d} Z$ in a stably stratified environment, but is dependent on the source buoyancy flux only to the quarter power.

The source size that is characterised by $\varGamma$ has a fairly strong impact on the height of rise, with significant decreases as the source size becomes larger. The ratio $N M_0/F_0$ is the momentum scaled by the buoyancy and stratification, and so is direct measure of the source strength, characterised here by $\tan \delta = N M_0/F_0$ in a stably stratified environment. Higher values of $\delta$ are associated with larger $M_0$ (until $\delta = {\rm \pi}/2$, where the source momentum is infinite) and result in significantly greater heights of rise.

The specific momentum $Q$ defined in (2.25) is determined at the source and retains its value as the thermal rises, and appears to be a conserved quantity so far undefined in the literature on thermal rise in stratified flows. It is a bulk quantity, and its internal contributions reflect the gradual change in balance between buoyancy and upward momentum, with upward momentum increasing when the thermal has positive buoyancy, and decreasing when the buoyancy is negative. Sources with non-zero buoyancy and zero momentum $\delta = 0$ are virtual sources for more realistic thermals having some momentum.

The assumption that the thermal is and remains of spherical shape is another simplification. A number of papers suggest that the shape is more of an oblate spheroid, but catering for another shape factor would not change the structure of the equations. Also, the thermal may begin spreading laterally after it reaches its level of zero buoyancy, but this is also not catered for here.

For some applications, knowledge of dilution is important. The rate of dilution of the effluent is defined by $D = ((\varGamma + 1 - f )/\varGamma )^{3/4}$ for a thermal in a stably stratified environment. As $f = -1$ at the top of rise, the dilution there is $D = (1 + 2/\varGamma ) ^ {3/4}$, and is therefore independent of $\delta$, the source strength, but dependent on the entrainment constant $\alpha$, since $\varGamma$ is inversely proportional to $\alpha$. This is an interesting and unexpected result, as it might be thought that increased momentum might enhance dilution through larger entrainment. Dilution is larger for smaller sources characterised by smaller $\varGamma$.

A question arises as to the relevance of the present results in unstably stratified environments. Such environments occur in the atmosphere in the early morning when solar heating of the Earth's surface heats the air immediately above, or perhaps more commonly when cooler air flows over a warmer ocean surface. Turner (1969) notes that the sustained motion of a thermal in an unstable environment is unlikely, but it remains possible that such circumstances may apply for a period short enough for a thermal to rise. That there do not appear to be data to compare with the theory is not ideal, however, any requirement that data be first available before a theory be published would appear to run counter to many scientific developments. This paper may prompt some ingenious new experiments.

For vertical forced plumes in an otherwise still environment, and for bent-over plumes in a crossflow, the mathematical structure of the buoyancy and momentum equations is the same as for thermals, although the scaling is different. For vertical forced plumes, the equation representing change in volume provides for a change in structure from jet-like spread to plume-like spread. This precludes analytical solutions; however, the entrainment hypothesis and the sinusoidal solutions for momentum and buoyancy ensure that such flows will also have similar properties throughout the range of parameters. For bent-over plumes in a crossflow, analytic solutions were found by Middleton (1986), and those solutions are analogous to the solutions found here for the thermal.

The simple assumptions made by Morton et al. (1956) have been adapted here for thermals emitted from finite size sources having momentum. The resulting simple analytical solutions determine thermals to remain straight sided at all stages of flow development, as is the case for asymptotic flows. The solutions for momentum and buoyancy have a sinusoidal structure for flows in stable environments, and a hyperbolic structure in unstable environments.