Hostname: page-component-f554764f5-rj9fg Total loading time: 0 Render date: 2025-04-21T06:20:53.339Z Has data issue: false hasContentIssue false
  • English
  • Français

Thermal effect in shock-induced gas filtration through porous media

Published online by Cambridge University Press:  22 November 2024

Jiarui Li Open the ORCID record for Jiarui Li [Opens in a new window] ,
Jun Chen ,
Baolin Tian Open the ORCID record for Baolin Tian [Opens in a new window] ,
Meizhen Xiang Open the ORCID record for Meizhen Xiang [Opens in a new window]  and
Kun Xue Open the ORCID record for Kun Xue [Opens in a new window]
Jiarui Li
Affiliation:
National Key Laboratory of Computational Physics, Institute of Applied Physics and Computational Mathematics, Beijing 100088, PR China State Key Laboratory of Explosive Science and Technology, Beijing Institute of Technology, Beijing 100081, PR China
Jun Chen
Affiliation:
National Key Laboratory of Computational Physics, Institute of Applied Physics and Computational Mathematics, Beijing 100088, PR China
Baolin Tian
Affiliation:
School of Aeronautic Science and Engineering, Beihang University, Beijing 100191, PR China
Meizhen Xiang
Affiliation:
National Key Laboratory of Computational Physics, Institute of Applied Physics and Computational Mathematics, Beijing 100088, PR China
Kun Xue*
Affiliation:
State Key Laboratory of Explosive Science and Technology, Beijing Institute of Technology, Beijing 100081, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

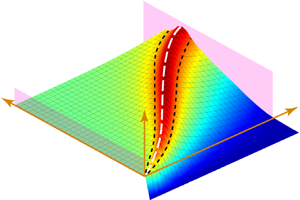
The gas dynamics of shock-induced gas filtration through densely packed granular columns with vastly varying shock intensity and the structural parameters are numerically investigated using a coupled Eulerian–Lagrangian approach. The results shed fundamental light on the thermal effects of the shock-induced gas filtration manifested by a distinctive self-heating hot gas layer traversing the medium. The characteristics of the thermal effects in terms of the thermal intensity and uniformity are found to vary with the shock Mach number, Ms, and the filtration coefficient of the granular media, Π. As the incident shock transitions from weak to strong, and (or) the filtration coefficient increases from O(10−5) to O(104), the heating mechanisms transition between three distinct heating modes. A phase diagram of heating modes is established on the parameter space (Ms, Π), which enables us to predict the characteristics of the thermal effect in different shock-induced gas filtrations. The thermal effects markedly accelerate the pressure diffusion due to the additional heat influx when the time scale of the former is smaller than or comparable to the latter. Based on the contour map displaying the coupling degree of the thermal effects and the pressure diffusion, we identify a decoupling criterion whereby the isothermal assumption holds if only the pressure diffusion is concerned. The thermal effects may well bring about considerable thermal shocks which pose a great threat to the integrity of the solid skeleton and further reduce the overall shock resistance performance of the porous media.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Compressible Flows: Shock waves Compressible Flows: Gas dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 999 , 25 November 2024 , A91
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abidoye, L.K., Khudaida, K.J. & Das, D.B. 2015 Geological carbon sequestration in the context of two-phase flow in porous media: a review. Crit. Rev. Environ. Sci. Technol. 45, 1105–1147.CrossRefGoogle Scholar
Alobaid, F. & Epple, B. 2013 Improvement, validation and application of CFD/DEM model to dense gas–solid flow in a fluidized bed. Particuology 11, 514–526.CrossRefGoogle Scholar
Apte, S., Mahesh, K. & Lundgren, T. 2003 A Eulerlan-Lagrangian model to simulate two-phase/particulate flows. Center for Turbulence Research Annual Research Briefs, pp. 161–171.Google Scholar
Baer, M.R. & Nunziato, J.W. 1986 A two-phase mixture theory for the deflagration-to-detonation transition (DDT) in reactive granular materials. Intl J. Multiphase Flow 12, 861–889.CrossRefGoogle Scholar
Balachandar, S. 2012 Recent advances in compressible multiphase flows explosive dispersal of particles. In Future Directions in CFD Research, a Modeling and Simulation Conference, Hampton.Google Scholar
Bdzil, J.B., Menikoff, R., Son, S.F., Kapila, A.K. & Stewart, D.S. 1999 Two-phase modeling of deflagration-to-detonation transition in granular materials: a critical examination of modeling issues. Phys. Fluids 11, 378–402.CrossRefGoogle Scholar
Bear, J. & Alexander, H.-D.C. 2010 Modeling Groundwater Flow and Contaminant Transport, 1st edn. Springer.CrossRefGoogle Scholar
Ben-Dor, G., Britan, A., Elperin, T., Igra, O. & Jiang, J.P. 1997 Experimental investigation of the interaction between weak shock waves and granular layers. Exp. Fluids 22, 432–443.CrossRefGoogle Scholar
Ben-Dor, G., Mazor, G., Igra, O., Sorek, S. & Onodera, H. 1994 Shock wave interaction with cellular materials. Shock Waves 3, 167–179.CrossRefGoogle Scholar
Borchardt-Ott, W. 2012 Crystallography: An Introduction. Springer.CrossRefGoogle Scholar
Britan, A., Ben-Dor, G., Elperin, T., Igra, O. & Jiang, J.P. 1997 Gas filtration during the impact of weak shock waves on granular layers. Intl J. Multiphase Flow 23, 473–491.CrossRefGoogle Scholar
Britan, A., Ben-Dor, G., Igra, O. & Shapiro, H. 2001 Shock waves attenuation by granular filters. Intl J. Multiphase Flow 27, 617–634.CrossRefGoogle Scholar
Britan, A., Ben-Dor, G., Igra, O. & Shapiro, H. 2006 Development of a general approach for predicting the pressure fields of unsteady gas flows through granular media. J. Appl. Phys. 99, 093519.CrossRefGoogle Scholar
Britan, A., Shapiro, H. & Ben-Dor, G. 2007 The contribution of shock tubes to simplified analysis of gas filtration through granular media. J. Fluid Mech. 586, 147–176.CrossRefGoogle Scholar
Britan, A., Shapiro, H., Liverts, M., Ben-Dor, G., Chinnayya, A. & Hadjadj, A. 2013 Macro-mechanical modelling of blast wave mitigation in foams. Part I. Review of available experiments and models. Shock Waves 23, 5–23.CrossRefGoogle Scholar
Carmouze, Q., Saurel, R., Chiapolino, A. & Lapebie, E. 2020 Riemann solver with internal reconstruction (RSIR) for compressible single-phase and non-equilibrium two-phase flows. J. Comput. Phys. 408, 109176.CrossRefGoogle Scholar
Chiapolino, A. & Saurel, R. 2020 Numerical investigations of two-phase finger-like instabilities. Comput. Fluids 206, 104585.CrossRefGoogle Scholar
Choi, D. & Park, H. 2022 Flow–structure interaction of a starting jet through a flexible circular nozzle. J. Fluid Mech. 949, A39.CrossRefGoogle Scholar
Crowe, C.T., Schwarzkopf, J.D., Sommerfeld, M. & Tsuji, Y. 2012 Multiphase Flows with Droplets and Particles. CRC Press.Google Scholar
De Paoli, M., Zonta, F. & Soldati, A. 2016 Influence of anisotropic permeability on convection in porous media: implications for geological CO2 sequestration. Phys. Fluids 28, 056601.CrossRefGoogle Scholar
Del Prete, E., Chinnayya, A., Domergue, L., Hadjadj, A. & Haas, J.F. 2013 Blast wave mitigation by dry aqueous foams. Shock Waves 23, 39–53.CrossRefGoogle Scholar
Di Felice, R. 1994 The voidage function for fluid-particle interaction systems. Intl J. Multiphase Flow 20, 153–159.CrossRefGoogle Scholar
Ergun, S. 1952 Fluid flow through packed columns. Chem. Engng Prog. 48, 89–94.Google Scholar
Eriksen, F.K., Toussaint, R., Turquet, A.L., Måløy, K.J. & Flekkøy, E.G. 2018 Pressure evolution and deformation of confined granular media during pneumatic fracturing. Phys. Rev. E 97, 012908.CrossRefGoogle ScholarPubMed
Feng, Y., Xu, B., Zhang, S., Yu, A. & Zulli, P. 2004 Discrete particle simulation of gas fluidization of particle mixtures. AIChE J. 50, 1713–1728.CrossRefGoogle Scholar
Flekkøy, E.G., Sandnes, B. & Måløy, K.J. 2023 Shape of a frictional fluid finger. Phys. Rev. Fluids 8, 114302.CrossRefGoogle Scholar
Frost, D.L. 2018 Heterogeneous/particle-laden blast waves. Shock Waves 28, 439–449.CrossRefGoogle Scholar
Gubin, S.A. 2018 Shock waves in porous media J. Phys.: Conf. Ser. 1099, 012015.Google Scholar
Guo, Y., Wassgren, C., Hancock, B., Ketterhagen, W. & Curtis, J. 2015 Computational study of granular shear flows of dry flexible fibres using the discrete element method. J. Fluid Mech. 775, 24–52.CrossRefGoogle Scholar
Gvozdeva, L., Faresov, Y.M. & Fokeev, V. 1985 Interaction between air shock wave and porous compressible material. Sov. Phys. Appl. Math. Tech. Phys. 3, 111–115.Google Scholar
Han, P., Xue, K. & Bai, C. 2021 Explosively driven dynamic compaction of granular media. Phys. Fluids 33, 023309.CrossRefGoogle Scholar
Hayek, M. 2017 A model for subsurface oil pollutant migration. Transp. Porous Media 120, 373–393.CrossRefGoogle Scholar
Henderson, L., Virgona, R., Di, J. & Gvozdeva, L. 1990 Refraction of a normal shock wave from nitrogen into polyurethane foam. AIP Conf. Proc. 208, 814–818.CrossRefGoogle Scholar
Ji, S., Li, P. & Chen, X. 2012 Experiments on shock-absorbing capacity of granular matter under impact load. Acta Phys. Sin. 61, 184703–184703.Google Scholar
Jiang, Y., Guo, Y., Yu, Z., Hua, X., Lin, J., Wassgren, C.R. & Curtis, J.S. 2021 Discrete element method-computational fluid dynamics analyses of flexible fibre fluidization. J. Fluid Mech. 910, A8.CrossRefGoogle Scholar
Kafui, K.D., Thornton, C. & Adams, M.J. 2002 Discrete particle-continuum fluid modelling of gas–solid fluidised beds. Chem. Engng Sci. 57, 2395–2410.CrossRefGoogle Scholar
Kalenko, S. & Liberzon, A. 2020 Particle-turbulence interaction of high Stokes number irregular shape particles in accelerating flow: a rocket-engine model. Intl J. Multiphase Flow. 133, 103451.CrossRefGoogle Scholar
Koneru, R.B., Rollin, B., Durant, B., Ouellet, F. & Balachandar, S. 2020 A numerical study of particle jetting in a dense particle bed driven by an air-blast. Phys. Fluids 32, 093301.CrossRefGoogle Scholar
Kruggel-Emden, H., Sturm, M., Wirtz, S. & Scherer, V. 2008 Selection of an appropriate time integration scheme for the discrete element method (DEM). Comput. Chem. Engng 32, 2263–2279.CrossRefGoogle Scholar
Lage, J.L. 1998 The fundamental theory of flow through permeable media. From Darcy to turbulence. In Transport Phenomena in Porous Media (eds. Ingham, D.B. & Pop, I.), pp. 1–30. Pergamon.Google Scholar
Levy, A., Ben-Dor, G., Skews, B.W. & Sorek, S. 1993 Head-on collision of normal shock waves with rigid porous materials. Exp. Fluids 15, 183–190.CrossRefGoogle Scholar
Li, J., Xue, K., Zeng, J., Tian, B. & Guo, X. 2021 Shock-induced interfacial instabilities of granular media. J. Fluid Mech. 930, A22.Google Scholar
Li, J., Zeng, J. & Xue, K. 2023 Pressure evolution in shock-compacted granular media. Pet. Sci. 20, 3736–3751.CrossRefGoogle Scholar
Liu, X., Osher, S. & Chan, T. 1994 Weighted essentially non-oscillatory schemes. J. Comput. Phys. 115, 200–212.CrossRefGoogle Scholar
Meng, B., Zeng, J., Tian, B., Li, L., He, Z. & Guo, X. 2019 Modeling and verification of the Richtmyer–Meshkov instability linear growth rate of the dense gas-particle flow. Phys. Fluids 31, 074102.CrossRefGoogle Scholar
Mo, H., Lien, F.S., Zhang, F. & Cronin, D.S. 2019 A mesoscale study on explosively dispersed granular material using direct simulation. J. Appl. Phys. 125, 214302.CrossRefGoogle Scholar
Morrison, F.A. 1972 Transient gas flow in a porous column. Ind. Engng Chem. Res. Fundam. 11, 191–197.CrossRefGoogle Scholar
O'Rourke, P.J. & Snider, D.M. 2010 An improved collision damping time for MP-PIC calculations of dense particle flows with applications to polydisperse sedimenting beds and colliding particle jets. Chem. Engng Sci. 65, 6014–6028.CrossRefGoogle Scholar
Osnes, A.N., Vartdal, M. & Pettersson Reif, B.A. 2017 Numerical simulation of particle jet formation induced by shock wave acceleration in a Hele-Shaw cell. Shock Waves 28, 451–461.CrossRefGoogle Scholar
Patankar, N.A. & Joseph, D.D. 2001 Modeling and numerical simulation of particulate flows by the Eulerian-Lagrangian approach. Intl J. Multiphase Flow 27, 1659–1684.CrossRefGoogle Scholar
Pathak, S. & Singh, T. 2015 An analytic solution of mathematical model of boussinq's equation in homogeneous porous media during infiltration of groundwater flow. J. Geogr. Environ. Earth Sci. Intl 3, 8.Google Scholar
Petel, O.E., Jetté, F.X., Goroshin, S., Frost, D.L. & Ouellet, S. 2011 Blast wave attenuation through a composite of varying layer distribution. Shock Waves 21, 215–224.CrossRefGoogle Scholar
Petitpas, F., Franquet, E., Saurel, R. & Le Metayer, O. 2007 A relaxation-projection method for compressible flows. Part II. Artificial heat exchanges for multiphase shocks. J. Comput. Phys. 225, 2214–2248.CrossRefGoogle Scholar
Pontalier, Q., Loiseau, J., Goroshin, S. & Frost, D.L. 2018 Experimental investigation of blast mitigation and particle–blast interaction during the explosive dispersal of particles and liquids. Shock Waves 28, 489–511.CrossRefGoogle Scholar
Qiao, T., Liu, L. & Ji, S. 2022 Superquadric DEM-SPH coupling method for interaction between non-spherical granular materials and fluids. Particuology 71, 20–33.CrossRefGoogle Scholar
Ram, O. & Sadot, O. 2015 Analysis of the pressure buildup behind rigid porous media impinged by shock waves in time and frequency domains. J. Fluid Mech. 779, 842–858.CrossRefGoogle Scholar
Rogg, B., Hermann, D. & Adomeit, G. 1985 Shock-induced flow in regular arrays of cylinders and packed beds. Intl J. Heat Mass Transfer 28, 2285–2298.CrossRefGoogle Scholar
Rogue, X., Rodriguez, G., Haas, J.-F. & Saurel, R. 1998 Experimental and numerical investigation of the shock-induced fluidization of a particles bed. Shock Waves 8, 29–45.CrossRefGoogle Scholar
Sadot, O., Ram, O., Ben-Dor, G., Levy, A., Golan, G., Ran, E. & Aizik, F. 2013 A simple constitutive model for predicting the pressure histories developed behind rigid porous media impinged by shock waves. J. Fluid Mech. 718, 507–523.Google Scholar
Saurel, R., Chinnayya, A. & Carmouze, Q. 2017 Modelling compressible dense and dilute two-phase flows. Phys. Fluids 29, 063301.CrossRefGoogle Scholar
Shen, H., Huang, Y., Illman, W.A., Su, Y. & Miao, K. 2023 Migration behaviour of LNAPL in fractures filled with porous media: laboratory experiments and numerical simulations. J. Contam. Hydrol. 253, 104118.CrossRefGoogle ScholarPubMed
Skews, B. 1991 The reflected pressure field in the interaction of weak shock waves with a compressible foam. Shock Waves 1, 205–211.CrossRefGoogle Scholar
Skews, B.W. 2001 Shock wave propagation in multi-phase media. Handbook of Shock Waves, pp. 545–596. Academic Press.CrossRefGoogle Scholar
Skews, B.W., Atkins, M.D. & Seitz, M.W. 1992 Gas dynamic and physical behaviour of compressible porous foams struck by a weak shock wave. In Shock Waves (ed. Takayama, K.), pp. 511–516. Springer.CrossRefGoogle Scholar
Smith, P. 2010 Blast walls for structural protection against high explosive threats: a review. Intl J. Prot. Struct. 1, 67–84.CrossRefGoogle Scholar
Snider, D.M., Clark, S.M. & O'Rourke, P.J. 2011 Eulerian–Lagrangian method for three-dimensional thermal reacting flow with application to coal gasifiers. Chem. Engng Sci. 66, 1285–1295.CrossRefGoogle Scholar
Sundaresan, S., Ozel, A. & Kolehmainen, J. 2018 Toward constitutive models for momentum, species, and energy transport in gas–particle flows. Annu. Rev. Chem. Biomol. Engng 9, 61–81.CrossRefGoogle ScholarPubMed
Tian, B., Zeng, J., Meng, B., Chen, Q., Guo, X. & Xue, K. 2020 Compressible multiphase particle-in-cell method (CMP-PIC) for full pattern flows of gas-particle system. J. Comput. Phys. 418, 109602.CrossRefGoogle Scholar
Toro, E.F. 2013 Riemann Solvers and Numerical Methods for Fluid Dynamics || The HLL and HLLC Riemann Solvers. Springer.Google Scholar
Ukai, S., Balakrishnan, K. & Menon, S. 2010 On Richtmyer–Meshkov instability in dilute gas-particle mixtures. Phys. Fluids 22, 104103.CrossRefGoogle Scholar
Vivek, P. & Sitharam, T.G. 2019 Granular Materials Under Shock and Blast Loading, 1st edn. Springer.Google Scholar
Xue, K., Miu, L., Li, J., Bai, C. & Tian, B. 2023 Explosive dispersal of granular media. J. Fluid Mech. 959, A17.CrossRefGoogle Scholar
Xue, K., Shi, X., Zeng, J., Tian, B., Han, P., Li, J., Liu, L., Meng, B., Guo, X. & Bai, C. 2020 Explosion-driven interfacial instabilities of granular media. Phys. Fluids 32, 084104.CrossRefGoogle Scholar
Xue, L., Li, D., Nan, T. & Wu, J. 2019 Predictive assessment of groundwater flow uncertainty in multiscale porous media by using truncated power variogram model. Transp. Porous Media 126, 97–114.CrossRefGoogle Scholar
Yan, G., Yu, H. & Mcdowell, G. 2009 Simulation of granular material behaviour using DEM. Procedia Earth Planet. Sci. 1, 598–605.CrossRefGoogle Scholar
Yin, J., Ding, J., Luo, X. & Yu, X. 2019 Numerical study on shock–dusty gas cylinder interaction. Acta Mechanica Sin. 35, 740–749.CrossRefGoogle Scholar
Yin, L., Ni, Z., Liu, J., Fan, F., Zhi, X., Ye, J., Pan, Y. & Guo, Y. 2023 High-temperature mechanical properties of constructional 6082-T6 aluminum alloy extrusion. Structures 48, 1244–1258.CrossRefGoogle Scholar