Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T16:41:59.488Z Has data issue: false hasContentIssue false
  • English
  • Français

Thermal convection in inclined cylindrical containers

Published online by Cambridge University Press:  11 February 2016

Olga Shishkina  and
Susanne Horn Open the ORCID record for Susanne Horn [Opens in a new window]
Olga Shishkina*
Affiliation:
Max Planck Institute for Dynamics and Self-Organization, Am Fassberg 17, 37077 Göttingen, Germany
Susanne Horn
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

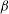By means of direct numerical simulations (DNS) we investigate the effect of a tilt angle ${\it\beta}$, 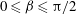$0\leqslant {\it\beta}\leqslant {\rm\pi}/2$, of a Rayleigh–Bénard convection (RBC) cell of aspect ratio 1, on the Nusselt number 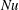$\mathit{Nu}$ and Reynolds number 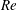$\mathit{Re}$. The considered Rayleigh numbers 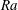$\mathit{Ra}$ range from 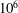$10^{6}$ to 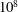$10^{8}$, the Prandtl numbers range from 0.1 to 100 and the total number of the studied cases is 108. We show that the 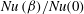$\mathit{Nu}\,({\it\beta})/\mathit{Nu}(0)$ dependence is not universal and is strongly influenced by a combination of 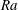$\mathit{Ra}$ and 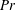$\mathit{Pr}$. Thus, with a small inclination 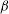${\it\beta}$ of the RBC cell, the Nusselt number can decrease or increase, compared to that in the RBC case, for large and small 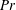$\mathit{Pr}$, respectively. A slight cell tilt may not only stabilize the plane of the large-scale circulation (LSC) but can also enforce an LSC for cases when the preferred state in the perfect RBC case is not an LSC but a more complicated multiple-roll state. Close to 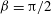${\it\beta}={\rm\pi}/2$, 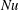$\mathit{Nu}$ and 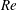$\mathit{Re}$ decrease with increasing 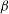${\it\beta}$ in all considered cases. Generally, the 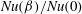$\mathit{Nu}({\it\beta})/\mathit{Nu}(0)$ dependence is a complicated, non-monotonic function of 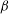${\it\beta}$.

JFM classification

Convection: Convection Convection: Convection in cavities
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 790 , 10 March 2016 , R3
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Brown, E. & Nikolaenko, A. 2006 The search for slow transients, and the effect of imperfect vertical alignment, in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 557, 347–367.CrossRefGoogle Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Bodenschatz, E., Pesch, W. & Ahlers, G. 2000 Recent developments in Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 32, 709–778.CrossRefGoogle Scholar
Bosbach, J., Weiss, S. & Ahlers, G. 2012 Plume fragmentation by bulk interactions in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 054501.CrossRefGoogle ScholarPubMed
Brown, E. & Ahlers, G. 2006 Rotations and cessations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 568, 351–386.Google Scholar
Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X.-Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.CrossRefGoogle Scholar
Chillà, F., Rastello, M., Chaumat, S. & Castaing, B. 2004 Long relaxation times and tilt sensitivity in Rayleigh–Bénard turbulence. Eur. Phys. J. B 40 (2), 223–227.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.CrossRefGoogle ScholarPubMed
Ciliberto, S., Cioni, S. & Laroche, C. 1996 Large-scale flow properties of turbulent thermal convection. Phys. Rev. E 54, R5901–R5904.Google Scholar
Cioni, S., Ciliberto, S. & Sommeria, J. 1997 Strongly turbulent Rayleigh–Bénard convection in mercury: comparison with results at moderate Prandtl number. J. Fluid Mech. 335, 111–140.Google Scholar
Frick, P., Khalilov, R., Kolesnichenko, I., Mamykin, A., Pakholkov, V., Pavlinov, A. & Rogozhkin, S. A. 2015 Turbulent convective heat transfer in a long cylinder with liquid sodium. Europhys. Lett. 109, 14002.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying view. J. Fluid Mech. 407, 27–56.Google Scholar
Guo, S.-X., Zhou, S.-Q., Cen, X.-R., Qu, L., Lu, Y.-Z., Sun, L. & Shang, X.-D. 2015 The effect of cell tilting on turbulent thermal convection in a rectangular cell. J. Fluid Mech. 762, 273–287.Google Scholar
Horn, S. & Shishkina, O. 2014 Rotating non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water. Phys. Fluids 26, 055111.Google Scholar
Horn, S. & Shishkina, O. 2015 Toroidal and poloidal energy in rotating Rayleigh–Bénard convection. J. Fluid Mech. 762, 232–255.Google Scholar
Horn, S., Shishkina, O. & Wagner, C. 2013 On non-Oberbeck–Boussinesq effects in three-dimensional Rayleigh–Bénard convection in glycerol. J. Fluid Mech. 724, 175–202.Google Scholar
Kolesnichenko, I. V., Mamykin, A. D., Pavlinov, A. M., Pakholkov, V. V., Rogozhkin, S. A., Frick, P. G., Khalilov, R. I. & Shepelev, S. F. 2015 Experimental study on free convection of sodium in a long cylinder. Therm. Engng 62, 414–422.CrossRefGoogle Scholar
Krishnamurti, R. 1970 On the transition to turbulent convection. Part 2. The transition to time-dependent flow. J. Fluid Mech. 42, 309–320.Google Scholar
Langebach, R. & Haberstroh, C. 2014 Natural convection in inclined pipes – a new correlation for heat transfer estimations. In AIP Conference Proceedings, vol. 1573, pp. 1504–1511.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
Ng, C. S., Ooi, A., Lohse, D. & Chung, D. 2015 Vertical natural convection: application of the unifying theory of thermal convection. J. Fluid Mech. 764, 349–361.Google Scholar
Roche, P.-E., Gauthier, F., Kaiser, R. & Salort, J. 2010 On the triggering of the ultimate regime of convection. New J. Phys. 12 (8), 085014.Google Scholar
Schlichting, H. & Gersten, K. 2000 Boundary-Layer Theory, 8th edn. Springer.Google Scholar
Shishkina, O., Horn, S. & Wagner, S. 2013 Falkner–Skan boundary layer approximation in Rayleigh–Bénard convection. J. Fluid Mech. 730, 442–463.Google Scholar
Shishkina, O., Horn, S., Wagner, S. & Ching, E. S. C. 2015 Thermal boundary layer equation for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 114, 114302.Google Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12, 075022.Google Scholar
Shishkina, O. & Wagner, S. 2016 Prandtl-number dependence of heat transport in laminar horizontal convection. Phys. Rev. Lett. 116, 024302.CrossRefGoogle ScholarPubMed
Shishkina, O., Wagner, S. & Horn, S. 2014 Influence of the angle between the wind and the isothermal surfaces on the boundary layer structures in turbulent thermal convection. Phys. Rev. E 89, 033014.Google Scholar
Siggia, E. 1994 High Rayleigh number convection. Annu. Rev. Fluid Mech. 26, 137–168.Google Scholar
Sun, C., Xi, H.-D. & Xia, K.-Q. 2005 Azimuthal symmetry, flow dynamics, and heat transport in turbulent thermal convection in a cylinder with an aspect ratio of 0.5. Phys. Rev. Lett. 95, 074502.Google Scholar
Vasilev, A. Yu., Kolesnichenko, I. V., Mamykin, A. D., Frick, P. G., Khalilov, R. I., Rogozhkin, S. A. & Pakholkov, V. V. 2015 Turbulent convective heat transfer in an inclined tube filled with sodium. Tech. Phys. 60, 1063–7842.Google Scholar
Wei, P., Weiss, S. & Ahlers, G. 2015 Multiple transitions in rotating turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 114, 114506.Google Scholar
Wei, P. & Xia, K.-Q. 2013 Viscous boundary layer properties in turbulent thermal convection in a cylindrical cell: the effect of cell tilting. J. Fluid Mech. 720, 140–168.Google Scholar
Weiss, S. & Ahlers, G. 2013 Effect of tilting on turbulent convection: cylindrical samples with aspect ratio ${\it\gamma}=0.50$ . J. Fluid Mech. 715, 314–334.Google Scholar