Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-29T04:36:22.576Z Has data issue: false hasContentIssue false
  • English
  • Français

Temporally resolved measurements of heavy, rigid fibre translation and rotation in nearly homogeneous isotropic turbulence

Published online by Cambridge University Press:  02 February 2017

L. Sabban ,
A. Cohen  and
R. van Hout
L. Sabban
Affiliation:
Faculty of Mechanical Engineering, Technion-Israel Institute of Technology, Haifa 32000, Israel
A. Cohen
Affiliation:
Faculty of Mechanical Engineering, Technion-Israel Institute of Technology, Haifa 32000, Israel
R. van Hout*
Affiliation:
Faculty of Mechanical Engineering, Technion-Israel Institute of Technology, Haifa 32000, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

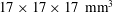A two orthogonal view, holographic cinematography system (volume of $17\times 17\times 17~\text{mm}^{3}$) was used to measure three-dimensional fibre translational velocities, orientations and rotation rates in near homogeneous isotropic air turbulence (HIT). Flow characteristics were determined from temporally resolved particle image velocimetry measurements. Two sets of rigid, nylon fibres having the same nominal length (0.5 mm) but different diameters (13.7 and 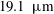$19.1~\unicode[STIX]{x03BC}\text{m}$), were released in near HIT at a Taylor microscale Reynolds number of 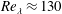$Re_{\unicode[STIX]{x1D706}}\approx 130$ and tracked at more than five times the Kolmogorov frequency. The ratio of fibre length to the Kolmogorov length scale was 2.8 and the two sets were characterized by Stokes numbers of 1.35 and 2.44, respectively. As a result of increased inertia, the probability density functions (PDFs) of the fluctuating fibre translational velocities were narrower than the ones of the air and the fibre velocity autocorrelations decreased at a decreasing rate. While fibre orientations in the cameras’ frame of reference were random as a result of the strong turbulence, it was shown that fibres align with the flow to minimize drag. PDFs of the fibre rotation rates indicated the occurrence of extreme rotation rate events. Furthermore, increasing inertia lowered the normalized, mean squared fibre rotation rates in comparison to results obtained for neutrally buoyant fibres having the same aspect ratio and including the effect of preferential alignment. The present results compare well to direct numerical simulations including the effect of fibre inertia.

JFM classification

Turbulent Flows: Isotropic turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 814 , 10 March 2017 , pp. 42 - 68
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bellani, G., Byron, M. L., Collignon, A. G., Meyer, C. R. & Variano, E. A. 2012 Shape effects on turbulent modulation by large nearly neutrally buoyant particles. J. Fluid Mech. 712, 41–60.Google Scholar
Benedict, L. H. & Gould, R. D. 1996 Towards better uncertainty estimates for turbulence statistics. Exp. Fluids 22, 129–136.Google Scholar
Bernstein, O. & Shapiro, M. 1994 Direct determination of the orientation distribution function of cylindrical particles immersed in laminar and turbulent shear flows. J. Aero. Sci. 25 (1), 113–136.Google Scholar
Boillot, A. & Prasad, A. 1996 Optimization procedure for pulse separation in cross-correlation PIV. Exp. Fluids 21, 87–93.Google Scholar
Bragg, G. M., van Zuiden, L. & Hermance, C. E. 1974 The free fall of cylinders at intermediate Reynolds number. Atmos. Environ. 8, 755–764.Google Scholar
Capone, A. & Romano, G. P. 2015 Interactions between fluid and fibres in a turbulent backward-facing step flow. Phys. Fluids 27, 053303.Google Scholar
Capone, A., Romano, G. P. & Soldati, A. 2015 Experimental investigation on interaction among fluid and rod-like particles in a turbulent pipe jet by means of particle image velocimetry. Exp. Fluids 56 (1), 1–15.Google Scholar
Carlsson, A., Håkansson, K., Kvick, M., Lundell, F. & Söderberg, L. D. 2011 Evaluation of steerable filter for detection of fibers in flowing suspensions. Exp. Fluids 51, 987–996.Google Scholar
Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles Drops, and Particles. Academic.Google Scholar
Cox, R. G. 1965 The steady motion of a particle of arbitrary shape at small Reynolds numbers. J. Fluid Mech. 23 (4), 625–643.Google Scholar
Cox, R. G. 1970 The motion of long slender body in viscous fluid. Part 1. General theory. J. Fluid Mech. 44, 791–810.Google Scholar
Csanady, G. T. 1963 Turbulent diffusion of heavy particles in the atmosphere. J. Atmos. Sci. 20, 201–208.Google Scholar
Duda, R. O. & Hart, P. E. 1972 Use of Hough transform to detect lines and curves in pictures. Commun. ACM 15, 11–15.Google Scholar
Elghobashi, S. 1994 On predicting particle-laden turbulent flows. Appl. Sci. Res. 52, 309–329.Google Scholar
Ferrante, A. & Elghobashi, S. 2003 On the physical mechanisms of two-way coupling in particle-laden isotropic turbulence. Phys. Fluids 15 (2), 315–329.Google Scholar
Field, C. A. & Welsh, A. H. 2007 Bootstrapping clustered data. J. R. Statist. Soc. B 69, 369–390.Google Scholar
Green, P. J. & Silverman, B. W. 1993 Nonparametric Regression and Generalized Linear Models: A Roughness Penalty Approach. Chapman and Hall/CRC.Google Scholar
Gopalan, B., Malkiel, E. & Katz, J. 2008 Experimental investigation of turbulence diffusion of slightly buoyant droplets in locally isotropic turbulence. Phys. Fluids 20, 095102.Google Scholar
Gustavsson, K., Einarsson, J. & Mehlig, B. 2014 Tumbling of small axisymmetric particles in random and turbulent flows. Phys. Rev. Lett. 112, 014501.Google Scholar
Hoseini, A. A., Lundell, F. & Andersson, H. I. 2015 Finite-length effects on dynamical behavior of rod-like particles in wall-bounded flows. Intl J. Multiphase Flow 76, 13–21.CrossRefGoogle Scholar
van Hout, R., Sabban, L. & Cohen, A. 2013 The use of high-speed PIV and holographic cinematography in the study of fiber suspension flows. Acta Mech. 224, 2263–2280.Google Scholar
Hwang, W. & Eaton, J. K. 2004 Creating homogeneous and isotropic turbulence without a mean flow. Exp. Fluids 36 (3), 444–454.Google Scholar
Jayaweera, K. O. L. F. & Mason, B. J. 1965 The behaviour of freely falling cylinders and cones in a viscous fluid. J. Fluid Mech. 22 (4), 709–720.CrossRefGoogle Scholar
Jeffery, G. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 178–198.Google Scholar
de Jong, J., Cao, L., Woodward, S. H., Salazar, J. P. L. C., Collins, L. R. & Meng, H. 2009 Dissipation rate estimation from PIV in zero-mean isotropic turbulence. Exp. Fluids 46, 499–515.Google Scholar
Khayat, R. E. & Cox, R. G. 1989 Inertia effects on the motion of long slender bodies. J. Fluid Mech. 209, 435–462.Google Scholar
Kristjánsson, J. E., Edwards, J. M. & Mitchell, D. L. 2000 Impact of a new scheme for optical properties of ice crystals on climates of two GCMs. J. Geophys. Res. 105, 10063–10079.CrossRefGoogle Scholar
Krushkal, E. M. & Gallily, I. 1988 On the orientation distribution function of non-spherical aerosol particles in a general shear flow-II. The turbulent case. J. Aero. Sci 19 (2), 197–211.Google Scholar
Lavoie, P., Avallone, G., De Gregorio, F., Romano, G. P. & Antonia, R. A. 2007 Spatial resolution of PIV for the measurement of turbulence. Exp. Fluids 43, 39–51.Google Scholar
Lundell, F., Söderberg, L. D. & Alfredsson, P. H. 2011 Fluid mechanics of papermaking. Annu. Rev. Fluid Mech. 43, 195–217.Google Scholar
Marchioli, C., Fantoni, M. & Soldati, A. 2010 Orientation, distribution, and deposition of elongated, inertial fibers in turbulent channel flow. Phys. Fluids 22, 033301.Google Scholar
Marchioli, C. & Soldati, A. 2013 Rotation statistics of fibers in wall shear turbulence. Acta Mech. 224, 2311–2329.Google Scholar
Marchioli, C., Zhao, L. & Andersson, H. 2016 On the relative motion between rigid fibres and fluid in turbulent channel flow. Phys. Fluids 28, 013301.Google Scholar
Marcus, G. G., Parsa, S., Kramel, S., Ni, R. & Voth, G. 2014 Measurements of the solid-body rotation of anisotropic particles in 3D turbulence. New J. Phys. 16, 102001.Google Scholar
Melling, A. 1997 Tracer particles and seeding for particle image velocimetry. Meas. Sci. Technol. 8, 1406–1416.Google Scholar
Milgram, J. H. & Li, W. 2002 Computational reconstruction of images from holograms. Appl. Opt. 41, 853–864.Google Scholar
Newsom, R. K. & Bruce, C. W. 1994 The Dynamics of fibrous aerosols in a quiescent atmosphere. Phys. Fluids 6, 521–530.Google Scholar
Newsom, R. K & Bruce, C. W. 1998 Orientational properties of fibrous aerosols in atmospheric turbulence. J. Aero. Sci. 29 (7), 773–797.CrossRefGoogle Scholar
Ni, R., Ouellette, N. T. & Voth, G. A. 2014 Alignment of vorticity and rods with Lagrangian fluid stretching in turbulence. J. Fluid Mech. 743, R3.Google Scholar
Nogueira, J., Lecuona, A. & Rodríguez, P. A. 1997 Data validation, false vectors correction and derived magnitudes calculation on PIV data. Meas. Sci. Technol. 8, 1493–1501.Google Scholar
Olson, J. A. 2001 The motion of fibres in turbulent flow, stochastic simulation of isotropic homogeneous turbulence. Intl J. Multiphase Flow 27 (12), 2083–2103.Google Scholar
Olson, J. A. & Kerekes, R. J. 1998 The motion of fibres in turbulent flow. J. Fluid Mech. 377, 47–64.Google Scholar
Ouellette, N. T., Xu, H. T. & Bodenschatz, E. 2006 A quantitative study of three-dimensional Lagrangian particle tracking algorithms. Exp. Fluids 40 (2), 301–313.Google Scholar
Papathanasiou, T. D. & Guell, D. C. 1997 Flow-induced Alignment in Composite Materials. Woodhead Publishing Ltd.Google Scholar
Parsa, S.2013 Rotational dynamics of rod particles in fluid flows. PhD dissertation, Wesleyan University, Middletown, CT.Google Scholar
Parsa, S., Calzavarini, E., Toschi, F. & Voth, G. A. 2012 Rotation rate of rods in turbulent fluid flow. Phys. Rev. Lett. 109, 134501.Google Scholar
Parsa, S., Guasto, J. S., Kishore, M., Ouellette, N. T., Gollub, J. P. & Voth, G. A. 2011 Rotation and alignment of rods in two-dimensional chaotic flow. Phys. Fluids 23, 043302.CrossRefGoogle Scholar
Parsheh, M., Brown, M. L. & Aidun, C. K. 2005 On the orientation of stiff fibres suspended in turbulent flow in a planar contraction. J. Fluid Mech. 545, 245–269.Google Scholar
Poelma, C., Westerweel, J. & Ooms, G. 2007 Particle–fluid interactions in grid-generated turbulence. J. Fluid Mech. 589, 315–351.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Pumir, A. & Wilkinson, M. 2011 Orientation statistics of small particles in turbulence. New J. Phys. 13, 093030.Google Scholar
Rabencov, B., Arca, J. & van Hout, R. 2014 Measurement of polystyrene beads suspended in a turbulent square channel flow: spatial distributions of velocity and number density. Intl J. Multiphase Flow 62, 110–122.Google Scholar
Reeks, M. W. 1977 On the dispersion of small particles suspended in an isotropic turbulent fluid. J. Fluid Mech. 83 (3), 529–546.Google Scholar
Sabban, L. & van Hout, R. 2011 Measurements of pollen grain dispersal in still air and stationary, near homogeneous, isotropic turbulence. J. Aero. Sci. 42 (12), 867–882.Google Scholar
Schnars, U. & Jueptner, W. 2005 Digital Holography. Springer.Google Scholar
Sheng, J., Malkiel, E. & Katz, J. 2006 Digital holographic microscope for measuring three-dimensional particle distributions and motions. Appl. Opt. 45, 3893–3901.Google Scholar
Shin, M. & Koch, D. L. 2005 Rotational and translational dispersion of fibres in isotropic turbulent flows. J. Fluid Mech. 540, 143–173.Google Scholar
Siewert, C., Kunnen, R. P. J., Meinke, M. & Schröder, W. 2014 Orientation statistics and settling velocity of ellipsoids in decaying turbulence. Atmos. Res. 142, 45–56.Google Scholar
Snyder, W. H. & Lumley, J. L. 1971 Some measurements of particle velocity autocorrelation functions in a turbulent flow. J. Fluid Mech. 48, 41–71.Google Scholar
Squires, K. D. & Eaton, J. K. 1991 Preferential concentration of particle by turbulence. Phys. Fluids A 3, 1169–1178.Google Scholar
Tanaka, T. & Eaton, J. K. 2007 A correction method for measuring turbulence kinetic energy dissipation rate by PIV. Exp. Fluids 42 (6), 893–902.Google Scholar
Tanaka, T. & Eaton, J. K. 2010 Sub-Kolmogorov resolution partical image velocimetry measurements of particle-laden forced turbulence. J. Fluid Mech. 643, 177–206.Google Scholar
Vikram, C. S. 1992 Particle Field Holography, Cambridge Studies in Modern Optics, vol. 11. Cambridge University Press.Google Scholar
van Wachem, B., Zastawny, M., Zhao, F. & Mallouppas, G. 2015 Modelling of gas–solid turbulent channel flow with non-spherical particles with large Stokes numbers. Intl J. Multiphase Flow 68, 80–92.Google Scholar
Yudine, M. I. 1959 Physical considerations on heavy-particle diffusion. From proceeding of the international symposium on atmospheric diffusion and air pollution. Adv. Geophys. 6, 185–191.Google Scholar
Zhang, H., Ahmadi, G., Fan, F. G. & Mclaughlin, J. B. 2001 Ellipsoidal particles transport and deposition in turbulent channel flows. Intl J. Multiphase Flow 27 (6), 971–1009.Google Scholar
Zhao, L., Challabotla, N. R., Andersson, H. I. & Variano, E. A. 2015 Rotation of nonspherical particles in turbulent channel flow. Phys. Rev. Lett. 115, 244501.Google Scholar
Zhao, L., Marchioli, C. & Andersson, H. I. 2014 Slip velocity of rigid fibers in turbulent channel flow. Phys. Fluids 26, 063302.Google Scholar