Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-29T04:38:09.441Z Has data issue: false hasContentIssue false
  • English
  • Français

Temperature dynamics in decaying isotropic turbulence with Joule heat production

Published online by Cambridge University Press:  29 April 2013

Dario De Marinis ,
Sergio Chibbaro ,
Marcello Meldi  and
Pierre Sagaut
Dario De Marinis
Affiliation:
Dipartimento di Meccanica, Matematica e Management, Politecnico di Bari, via Re David 200, 70125 Bari, Italy Institut Jean Le Rond d’Alembert, CNRS UMR 7190, 4 Place Jussieu, F-75252 Paris CEDEX 5, France
Sergio Chibbaro
Affiliation:
Institut Jean Le Rond d’Alembert, CNRS UMR 7190, 4 Place Jussieu, F-75252 Paris CEDEX 5, France Institut Jean Le Rond d’Alembert, Université Pierre et Marie Curie, Paris 6, 4 Place Jussieu F-75252 Paris CEDEX 5, France
Marcello Meldi*
Affiliation:
Institut Jean Le Rond d’Alembert, CNRS UMR 7190, 4 Place Jussieu, F-75252 Paris CEDEX 5, France Institut Jean Le Rond d’Alembert, Université Pierre et Marie Curie, Paris 6, 4 Place Jussieu F-75252 Paris CEDEX 5, France
Pierre Sagaut
Affiliation:
Institut Jean Le Rond d’Alembert, CNRS UMR 7190, 4 Place Jussieu, F-75252 Paris CEDEX 5, France Institut Jean Le Rond d’Alembert, Université Pierre et Marie Curie, Paris 6, 4 Place Jussieu F-75252 Paris CEDEX 5, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper presents an extension of existing works dealing with the dynamics of a passive scalar in freely decaying isotropic turbulence, by accounting for a production mechanism of the passive scalar itself. The physically relevant case of the temperature dynamics in the presence of Joule heating via the dissipation of the turbulent kinetic energy is selected and analysed by theoretical and numerical means. In particular, the sensitivity of the temperature decay to the non-dimensional parameters Prandtl number (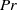$\mathit{Pr}$) and Eckert number (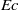$\mathit{Ec}$), the latter measuring the intensity of the internal energy production mechanism, is investigated. The time behaviour of the global quantities such as the temperature variance 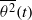$ \overline{{\theta }^{2} } (t)$ and its destruction rate 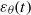${\varepsilon }_{\theta } (t)$ is analysed, and a detailed analysis of the temperature variance spectrum 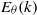${E}_{\theta } (k)$ is provided. In the case of a very strong heating mechanism, some important modifications of the temperature dynamics are observed. The time-decay-law exponents of the global physical quantities assume new values, which are governed only by features of the kinetic energy spectrum, while they depend on the shape of 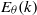${E}_{\theta } (k)$ in the classical free-decay case. The temperature variance spectrum 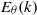${E}_{\theta } (k)$ exhibits two new spectral ranges. One is a convective–production range such that 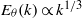${E}_{\theta } (k)\propto {k}^{1/ 3} $ is observed for a finite time at all values of 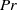$\mathit{Pr}$. In the case of very diffusive fluids with 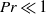$\mathit{Pr}\ll 1$, a convective–diffusive–production range with 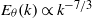${E}_{\theta } (k)\propto {k}^{- 7/ 3} $ is also detected.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 724 , 10 June 2013 , pp. 425 - 449
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

André, J. C. & Lesieur, M. 1977 Influence of helicity on high Reynolds number isotropic turbulence. J. Fluid Mech. 81, 187–207.Google Scholar
Antonia, R. A. & Orlandi, P. 2003 The Batchelor constant in decaying isotropic turbulence. Phys. Fluids 15, 2084–2086.CrossRefGoogle Scholar
Batchelor, G. K. 1959a Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113–133.CrossRefGoogle Scholar
Batchelor, G. K. 1959b Small-scale variation of convected quantities like temperature in turbulent fluid. Part 2. The case of large conductivity. J. Fluid Mech. 5, 134–139.Google Scholar
Bogucki, D., Domaradzki, J. A. & Yeung, P. K. 1997 Direct numerical simulations of passive scalars with $Pr\gt 1$ advected by turbulent flow. J. Fluid Mech. 343, 111–130.Google Scholar
Bos, W. J. T. & Bertoglio, J.-P. 2006 Dynamics of spectrally truncated inviscid turbulence. Phys. Fluids 18, 071701.CrossRefGoogle Scholar
Bos, W. J. T. & Bertoglio, J.-P. 2007 Inertial range scaling of scalar flux spectra in uniformly sheared turbulence. Phys. Fluids 19, 025104.Google Scholar
Bos, W. J. T., Rubinstein, R. & Fang, L. 2012 Reduction of mean-square advection in turbulent passive scalar mixing. Phys. Fluids 24, 075104.Google Scholar
Bos, W. J. T., Touil, H. & Bertoglio, J. P. 2005 Reynolds number dependency of the scalar flux spectrum in isotropic turbulence with a uniform scalar gradient. Phys. Fluids 17, 125108.Google Scholar
Chasnov, J., Canuto, V. M. & Rogallo, R. S. 1988 Turbulence spectrum of a passive temperature field: results of a direct numerical simulation. Phys. Fluids 31, 2065–2067.Google Scholar
Comte-Bellot, G. & Corrsin, S. 1966 The use of a contraction to improve the isotropy of grid-generated turbulence. J. Fluid Mech. 25, 657–682.CrossRefGoogle Scholar
Corrsin, S. 1951 On the spectrum of isotropic temperature fluctuations in an isotropic turbulence. J. Appl. Phys. 22 (4), 469–473.Google Scholar
Corrsin, S. 1961 The reactant concentration spectrum in turbulent mixing with a first-order reaction. J. Fluid Mech. 11, 407–416.CrossRefGoogle Scholar
Corrsin, S. 1964 Further generalization of Onsager’s cascade model for turbulent spectra. Phys. Fluids 7, 1156–1159.Google Scholar
Donzis, D. A., Sreenivasan, K. R. & Yeung, P. K. 2010 The Batchelor spectrum for mixing of passive scalars in isotropic turbulence. Flow Turbul. Combust. 85 (3), 549–566.Google Scholar
Driscoll, R. J. & Kennedy, L. A. 1984 A model for the spectrum of passive scalars in an isotropic turbulence field. Phys. Fluids 28, 72–80.Google Scholar
Gibson, C. H. 1968 Fine structure of scalar fields mixed by turbulence. II. Spectral theory. Phys. Fluids 11, 2316–2327.CrossRefGoogle Scholar
Gibson, C. H. & Schwarz, W. H. 1963 The universal equilibrium spectra of turbulent velocity and scalar fields. J. Fluid Mech. 16, 365–377.Google Scholar
Grant, H. L., Hughes, W. M., Vogel, W. M. & Moillet, A. 1968 The spectrum of temperature fluctuations in turbulent flow. J. Fluid Mech. 34, 423–442.CrossRefGoogle Scholar
Herr, S., Wang, L. P. & Collins, L. R. 1996 EDQNM model of a passive scalar with a uniform mean gradient. Phys. Fluids 8, 1588–1608.Google Scholar
Herring, J. R., Schertzer, D., Lesieur, M., Newman, G. R., Chollet, J. P. & Larcheveque, M. 1982 A comparative assessment of spectral closures as applied to passive scalar diffusion. J. Fluid Mech. 124, 411–437.Google Scholar
Kolmogorov, A. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds’ numbers. Akad. Nauk SSSR Dokl. 30, 301–305.Google Scholar
Kraichnan, R. H. 1968 Small-scale structure of a scalar field convected by turbulence. Phys. Fluids 11 (5), 945–953.Google Scholar
Krstulovic, G. & Brachet, M. E. 2008 Two-fluid model of the truncated Euler equations. Physica D 237, 2015–2019.Google Scholar
Lesieur, M. 2008 Turbulence in Fluids, 4th edn. Springer.Google Scholar
Lesieur, M., Montmory, C. & Chollet, J.-P. 1987 The decay of kinetic energy and temperature variance in three-dimensional isotropic turbulence. Phys. Fluids 30, 1278–1286.Google Scholar
Meldi, M. & Sagaut, P. 2012 On non-self similar regimes in homogeneous isotropic turbulence decay. J. Fluid Mech. 711, 364–393.CrossRefGoogle Scholar
Meldi, M., Sagaut, P. & Lucor, D. 2011 A stochastic view of isotropic turbulence decay. J. Fluid Mech. 668, 351–362.Google Scholar
Miller, P. L. & Dimotakis, P. E. 1996 Measurements of scalar power spectra in high Schmidt number turbulent jets. J. Fluid Mech. 308, 129–146.Google Scholar
Obukhov, A. M. 1949 Temperature field structure in a turbulent flow. Izv. Acad. Nauk SSSR Geogr. Geofiz 13, 58–69.Google Scholar
Obukhov, A. M. 1968 Structure of the temperature field in turbulent flow. Tech. Rep. Defense Technical Information Center Document.Google Scholar
Orszag, S. A. 1970 Analytical theories of turbulence. J. Fluid Mech. 41, 363–386.Google Scholar
Pao, Y. H. 1965 Structure of turbulent velocity and scalar fields at large wavenumbers. Phys. Fluids 8, 1063–1075.Google Scholar
Qian, J. 1986 Turbulent passive scalar field of a small Prandtl number. Phys. Fluids 29, 3586–3589.Google Scholar
Qian, J. 1990 The spectrum of a turbulent passive scalar in the viscous-convective range. J. Fluid Mech. 217, 203–212.Google Scholar
Rubinstein, R. & Clark, T. T. 2005 Self-similar turbulence evolution and the dissipation rate transport equation. Phys. Fluids 17, 095104.Google Scholar
Saffman, P. J. 1967 The large-scale structure of homogeneous turbulence. J. Fluid Mech. 27, 581–593.Google Scholar
Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence Dynamics. Cambridge University Press.Google Scholar
Schlichting, E. 1968 Boundary Layer Theory, 6th edn. McGraw-Hill.Google Scholar
Tchoufag, J., Sagaut, P. & Cambon, C. 2012 Spectral approach to finite Reynolds number effects on Kolmogorov’s $4/ 5$ law in isotropic turbulence. Phys. Fluids 24, 015107.Google Scholar
Ulitsky, M., Vaithianathan, T. & Collins, L. R. 2002 A spectral study of differential diffusion of passive scalars in isotropic turbulence. J. Fluid Mech. 460, 1–38.Google Scholar
Vignon, J. M. & Cambon, C. 1980 Thermal spectral calculation using Eddy Damped Quasi Normal Markovian theory. Phys. Fluids 23, 1935–1937.Google Scholar
Warhaft, Z. 2000 Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 32 (1), 203–240.Google Scholar
Warhaft, Z. & Lumley, J. L. 1978 An experimental study of the decay of temperature fluctuations in grid-generated turbulence. J. Fluid Mech. 88, 659–684.Google Scholar
Williams, R. M. & Paulson, C. A. 1977 Microscale temperature and velocity spectra in the atmospheric boundary layer. J. Fluid Mech. 83, 547–567.Google Scholar
Woodruff, S. L. & Rubinstein, R. 2006 Multiple-scale perturbation analysis of slowly evolving turbulence. J. Fluid Mech. 565, 95–103.Google Scholar
Xia, Y., Liu, Y., Vaithianathan, T. & Collins, L. R. 2010 Eddy Damped Quasi Normal Markovian theory for chemically reactive scalars in isotropic turbulence. Phys. Fluids 22, 045103.Google Scholar
Yeung, P. K. & Sreenivasan, K. R. 2013 Spectrum of passive scalars of high molecular diffusivity in turbulent mixing. J. Fluid Mech. 716, R14.CrossRefGoogle Scholar