Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-20T15:20:58.811Z Has data issue: false hasContentIssue false
  • English
  • Français

Taylor dispersion and thermal expansion effects on flame propagation in a narrow channel

Published online by Cambridge University Press:  30 July 2014

P. Pearce  and
J. Daou
P. Pearce*
Affiliation:
School of Mathematics, University of Manchester, Manchester M13 9PL, UK
J. Daou
Affiliation:
School of Mathematics, University of Manchester, Manchester M13 9PL, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the propagation of a premixed flame subject to thermal expansion through a narrow channel against a Poiseuille flow of large amplitude. This is the first study to consider the effect of a large-amplitude flow, characterised by a Péclet number of order one, 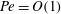$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Pe}=O(1)$, on a variable-density premixed flame in the asymptotic limit of a narrow channel. It is also the first study on Taylor dispersion in the context of combustion. The relationship between the propagation speed and Péclet number is investigated, with the effect of large flame-front thickness $\epsilon $ and activation energy 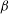$\beta $ studied asymptotically in an appropriate distinguished limit. The premixed flame for 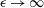$\epsilon \to \infty $, with 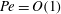$\mathit{Pe}=O(1)$, is found to be governed by the equation for a planar premixed flame with an effective diffusion coefficient. In this case the premixed flame can be considered to be in the Taylor regime of enhanced dispersion due to a parallel flow. The infinite activation energy limit 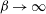$\beta \to \infty $ is taken to provide an analytical description of the propagation speed. Corresponding results are obtained for a premixed flame in the constant-density approximation. The asymptotic results are compared to numerical results obtained for selected values of $\epsilon $ and 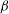$\beta $ and for moderately large values of the Péclet number. Physical reasons for the differences in propagation speed between constant- and variable-density flames are discussed. Finally, the asymptotic results are shown to agree with those of previous studies performed in the limit 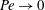$\mathit{Pe}\to 0$.

JFM classification

Reacting Flows: Combustion Reacting Flows: Flames Reacting Flows: Laminar reacting flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 754 , 10 September 2014 , pp. 161 - 183
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahn, J., Eastwood, C., Sitzki, L. & Ronney, P. D. 2005 Gas-phase and catalytic combustion in heat-recirculating burners. Proc. Combust. Inst. 30 (2), 2463–2472.Google Scholar
Aldredge, R. C. 1992 The propagation of wrinkled premixed flames in spatially periodic shear flow. Combust. Flame 90 (2), 121–133.Google Scholar
Bradley, D. 1992 How fast can we burn? In Symposium (International) on Combustion, vol. 24, pp. 247–262. Elsevier.Google Scholar
Brenner, H. & Edwards, D. A. 1993 Macrotransport Processes. Butterworth-Heinemann.Google Scholar
Clavin, P. & Williams, F. A. 1979 Theory of premixed-flame propagation in large-scale turbulence. J. Fluid Mech. 90 (3), 589–604.Google Scholar
Cui, C., Matalon, M., Daou, J. & Dold, J. 2004 Effects of differential diffusion on thin and thick flames propagating in channels. Combust. Theor. Model. 8 (1), 41–64.CrossRefGoogle Scholar
Damköhler, G. 1940 Influence of turbulence on the velocity flames in gas mixtures. Z. Elektrochem. 46, 601–626.Google Scholar
Daou, J., Dold, J. & Matalon, M. 2002 The thick flame asymptotic limit and Damköhler’s hypothesis. Combust. Theor. Model. 6 (1), 141–153.CrossRefGoogle Scholar
Daou, J. & Matalon, M. 2001 Flame propagation in Poiseuille flow under adiabatic conditions. Combust. Flame 124 (3), 337–349.Google Scholar
Daou, J. & Matalon, M. 2002 Influence of conductive heat-losses on the propagation of premixed flames in channels. Combust. Flame 128 (4), 321–339.Google Scholar
Daou, J. & Sparks, P. 2007 Flame propagation in a small-scale parallel flow. Combust. Theor. Model. 11 (5), 697–714.Google Scholar
Dentz, M., Tartakovsky, D. M., Abarca, E., Guadagnini, A., Sanchez-Vila, X. & Carrera, J. 2006 Variable-density flow in porous media. J. Fluid Mech. 561, 209–235.CrossRefGoogle Scholar
Deuflhard, P. 1974 A modified Newton method for the solution of ill-conditioned systems of nonlinear equations with application to multiple shooting. Numer. Math. 22 (4), 289–315.Google Scholar
Fan, A., Minaev, S., Kumar, S., Liu, W. & Maruta, K. 2007 Experimental study on flame pattern formation and combustion completeness in a radial microchannel. J. Micromech. Microengng 17 (12), 2398.Google Scholar
Felder, C., Oltean, C., Panfilov, M. & Buès, M. 2004 Dispersion de Taylor généralisée à un fluide à propriétés physiques variables. C. R. Méc. 332 (3), 223–229.Google Scholar
Fernandez-Pello, A. C. 2002 Micropower generation using combustion: issues and approaches. Proc. Combust. Inst. 29 (1), 883–899.Google Scholar
Kanury, A. M. 1975 Introduction to Combustion Phenomena: For Fire, Incineration, Pollution, and Energy Applications, vol. 2. Taylor & Francis.Google Scholar
Kerstein, A. R., Ashurst, W. T. & Williams, F. A. 1988 Field equation for interface propagation in an unsteady homogeneous flow field. Phys. Rev. A 37 (7), 2728–2731.Google Scholar
Kurdyumov, V. N. 2011 Lewis number effect on the propagation of premixed flames in narrow adiabatic channels: symmetric and non-symmetric flames and their linear stability analysis. Combust. Flame 158 (7), 1307–1317.Google Scholar
Kurdyumov, V. N. & Fernandez-Tarrazo, E. 2002 Lewis number effect on the propagation of premixed laminar flames in narrow open ducts. Combust. Flame 128 (4), 382–394.Google Scholar
Kurdyumov, V. N. & Matalon, M. 2013 Flame acceleration in long narrow open channels. Proc. Combust. Inst. 34 (1), 865–872.CrossRefGoogle Scholar
Leconte, M., Jarrige, N., Martin, J., Rakotomalala, N., Salin, D. & Talon, L. 2008 Taylor’s regime of an autocatalytic reaction front in a pulsative periodic flow. Phys. Fluids 20, 057102.Google Scholar
Oltean, C., Felder, Ch., Panfilov, M. & Buès, M. A. 2004 Transport with a very low density contrast in Hele–Shaw cell and porous medium: evolution of the mixing zone. Transp. Porous Media 55 (3), 339–360.CrossRefGoogle Scholar
Pearce, P. & Daou, J. 2013a The effect of gravity and thermal expansion on the propagation of a triple flame in a horizontal channel. Combust. Flame 160 (12), 2800–2809.Google Scholar
Pearce, P. & Daou, J. 2013b Rayleigh–Bénard instability generated by a diffusion flame. J. Fluid Mech. 736, 464–494.Google Scholar
Peters, N. 2000 Turbulent Combustion. Cambridge University Press.Google Scholar
Ronney, P. D. 1995 Some open issues in premixed turbulent combustion. In Modeling in Combustion Science (ed. Buckmaster, J. & Takeno, T.), pp. 1–22. Springer.Google Scholar
Shampine, L. F., Kierzenka, J. & Reichelt, M. W.2000 Solving boundary value problems for ordinary differential equations in MATLAB with BVP4C. Tech. Rep. The MathWorks.Google Scholar
Short, M. & Kessler, D. A. 2009 Asymptotic and numerical study of variable-density premixed flame propagation in a narrow channel. J. Fluid Mech. 638, 305–337.CrossRefGoogle Scholar
Sitzki, L., Borer, K., Schuster, E., Ronney, P. D. & Wussow, S.2001 Combustion in microscale heat-recirculating burners. In The Third Asia-Pacific Conference on Combustion, Seoul, Korea, vol. 6, pp. 11–14.Google Scholar
Sivashinsky, G. I. 1988 Cascade-renormalization theory of turbulent flame speed. Combust. Sci. Technol. 62 (1–3), 77–96.CrossRefGoogle Scholar
ATaylor, G. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. 219 (1137), 186–203.Google Scholar
Yakhot, V. 1988 Propagation velocity of premixed turbulent flames. Combust. Sci. Technol. 60 (1–3), 191–214.Google Scholar