Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T10:36:14.800Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetry reduction of turbulent pipe flows

Published online by Cambridge University Press:  17 August 2015

Francesco Fedele ,
Ozeair Abessi  and
Philip J. Roberts
Francesco Fedele*
Affiliation:
School of Civil and Environmental Engineering, Georgia Institute of Technology, Atlanta, GA 30322, USA School of Electrical and Computer Engineering, Georgia Institute of Technology, Atlanta, GA 30322, USA
Ozeair Abessi
Affiliation:
School of Civil Engineering, Babol Noshirvani University of Technology, Babol47148-71167, Iran
Philip J. Roberts
Affiliation:
School of Civil and Environmental Engineering, Georgia Institute of Technology, Atlanta, GA 30322, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

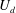We propose and apply a Fourier-based symmetry-reduction scheme to remove, or quotient, the streamwise translation symmetry of laser-induced-fluorescence measurements of turbulent pipe flows that are viewed as dynamical systems in a high-dimensional state space. We also explain the relation between Taylor’s hypothesis and the comoving frame velocity $U_{d}$ of the turbulent orbit in state space. In particular, in physical space we observe flow structures that deform as they advect downstream at a speed that differs significantly from 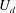$U_{d}$. Indeed, the symmetry-reduction analysis of planar dye concentration fields at Reynolds number 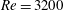$Re=3200$ reveals that the speed $u$ at which high-concentration peaks advect is roughly 1.43 times 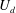$U_{d}$. In a physically meaningful symmetry-reduced frame, the excess speed 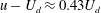$u-U_{d}\approx 0.43U_{d}$ can be explained in terms of the so-called geometric phase velocity 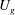$U_{g}$ associated with the orbit in state space. The ‘self-propulsion velocity’ 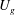$U_{g}$ is induced by the shape-changing dynamics of passive scalar structures observed in the symmetry-reduced frame, in analogy with that of a swimmer at low Reynolds numbers.

JFM classification

Mathematical Foundations: General fluid mechanics Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 779 , 25 September 2015 , pp. 390 - 410
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Banner, M. L., Barthelemy, X., Fedele, F., Allis, M., Benetazzo, A., Dias, F. & Peirson, W. L. 2014 Linking reduced breaking crest speeds to unsteady nonlinear water wave group behavior. Phys. Rev. Lett. 112, 114502.CrossRefGoogle ScholarPubMed
Berry, M. V. 1984 Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 392 (1802), 45–57.Google Scholar
Budanur, N. B., Cvitanović, P., Davidchack, R. L. & Siminos, E. 2015 Reduction of so(2) symmetry for spatially extended dynamical systems. Phys. Rev. Lett. 114, 084102.Google Scholar
Chandler, G. J. & Kerswell, R. R. 2013 Invariant recurrent solutions embedded in a turbulent two-dimensional Kolmogorov flow. J. Fluid Mech. 722, 554–595.CrossRefGoogle Scholar
Cvitanović, P. 2013 Recurrent flows: the clockwork behind turbulence. J. Fluid Mech. 726, 1–4.Google Scholar
Cvitanović, P., Artuso, R., Mainieri, R., Tanner, G. & Vattay, G. 2012 Chaos: Classical and Quantum. Niels Bohr Institute, Copenhagen, www.ChaosBook.org.Google Scholar
Cvitanović, P. & Eckhardt, B. 1991 Periodic orbit expansions for classical smooth flows. J. Phys. A: Math. Gen. 24 (5), L237.Google Scholar
Cvitanović, P. P., Borrero-Echeverry, D., Carroll, K. M., Robbins, B. & Siminos, E. 2012 Cartography of high-dimensional flows: a visual guide to sections and slices. Chaos 22, 047506.Google Scholar
Del Álamo, J. C. & Jimenez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.Google Scholar
Faisst, H. & Eckhardt, B. 2003 Traveling waves in pipe flow. Phys. Rev. Lett. 91 (22), 224502.Google Scholar
Fedele, F. 2014a Geometric phases of water waves. Europhys. Lett. 107 (69001).Google Scholar
Fedele, F. 2014b On certain properties of the compact Zakharov equation. J. Fluid Mech. 748, 692–711.Google Scholar
Froehlich, S. & Cvitanović, P. 2012 Reduction of continuous symmetries of chaotic flows by the method of slices. Commun. Nonlinear Sci. Numer. Simul. 17 (5), 2074–2084.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.Google Scholar
Gritsun, A. 2011 Connection of periodic orbits and variability patterns of circulation for the barotropic model of atmospheric dynamics. Dokl. Earth Sci. 438 (1), 636–640.Google Scholar
Gritsun, A. 2013 Statistical characteristics, circulation regimes and unstable periodic orbits of a barotropic atmospheric model. Phil. Trans. R. Soc. Lond. A 371 (1991).Google Scholar
Hannay, J. H. 1985 Angle variable holonomy in adiabatic excursion of an integrable hamiltonian. J. Phys. A: Math. Gen. 18 (2), 221.CrossRefGoogle Scholar
Hopf, H. 1931 Über die abbildungen der dreidimensionalen sphäre auf die kugelfläche. Math. Ann. 104 (1), 637–665.Google Scholar
Husemöller, D. 1994 Graduate Texts in Mathematics, 20, 3rd edn., vol. 1. Springer.Google Scholar
Kreilos, T., Zammert, S. & Eckhardt, B. 2014 Comoving frames and symmetry-related motions in parallel shear flows. J. Fluid Mech. 751, 685–697.Google Scholar
Krogstad, P.-Å., Kaspersen, J. H. & Rimestad, S. 1998 Convection velocities in a turbulent boundary layer. Phys. Fluids 10 (4), 949–957.CrossRefGoogle Scholar
Pancharatnam, S. 1956 Generalized theory of interference, and its applications. Proc. Indian Acad. Sci. A 44 (5), 247–262.Google Scholar
Roweis, S. T. & Saul, L. K. 2000 Nonlinear dimensionality reduction by locally linear embedding. Science 290 (5500), 2323–2326.CrossRefGoogle ScholarPubMed
Rowley, C. W., Kevrekidis, I. G., Marsden, J. E. & Lust, K. 2003 Reduction and reconstruction for self-similar dynamical systems. Nonlinearity 16 (4), 1257.Google Scholar
Rowley, C. W. & Marsden, J. E. 2000 Reconstruction equations and the Karhunen–Loève expansion for systems with symmetry. Physica D 142 (1–2), 1–19.Google Scholar
Samuel, J. & Bhandari, R. 1988 General setting for Berry’s phase. Phys. Rev. Lett. 60, 2339–2342.Google Scholar
Shapere, A. & Wilczek, F. 1989 Geometry of self-propulsion at low Reynolds number. J. Fluid Mech. 198, 557–585.Google Scholar
Siminos, E. & Cvitanović, P. 2011 Continuous symmetry reduction and return maps for high-dimensional flows. Physica D 240 (2), 187–198.Google Scholar
Simon, B. 1983 Holonomy, the quantum adiabatic theorem, and Berry’s phase. Phys. Rev. Lett. 51 (24), 2167–2170.Google Scholar
Steenrod, N. 1999 The Topology of Fibre Bundles. Princeton University Press.Google Scholar
Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. A 164 (919), 476–490.Google Scholar
Tian, X. & Roberts, P. J. 2003 A 3D lif system for turbulent buoyant jet flows. Exp. Fluids 35 (6), 636–647.CrossRefGoogle Scholar
Viswanath, D. 2007 Recurrent motions within plane Couette turbulence. J. Fluid Mech. 580, 339–358.CrossRefGoogle Scholar
Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.Google Scholar
Willis, A. P., Cvitanović, P. & Avila, M. 2013 Revealing the state space of turbulent pipe flow by symmetry reduction. J. Fluid Mech. 721, 514–540.CrossRefGoogle Scholar